Eins-zu-eins-funktionen

Mit diesem Rechner können Sie beurteilen, ob eine Funktion eins-zu-eins ist oder nicht, wobei alle Schritte angezeigt werden. Als Erstes müssen Sie die Funktion angeben. Das kann etwas einfaches, lineares oder quadratisches sein wie "y = x^2 - 1", oder Sie können sich für eine rationale Funktion wie "f(x) = (x-1)/(x+3)".

Wenn Sie mit Ihren Angaben zufrieden sind und sich vergewissert haben, dass die Funktion gültig ist, klicken Sie auf die Schaltfläche "Berechnen", damit Ihnen alle Schritte des Prozesses angezeigt werden.

Das Konzept der Eins-zu-Eins-Funktion ist in der Algebra und der Infinitesimalrechnung sehr wichtig. Es gibt viele einfache Möglichkeiten, auf Eins-zu-Eins zu testen, eine davon ist die Horizontaler Linientest aber aufgrund ihrer Beschaffenheit ist es einfacher, zu beweisen, dass eine Funktion eins-zu-eins ist. Um zu beweisen, dass eine Funktion eineindeutig ist, benötigen wir eine lösen von Gleichungen analytischer Prozess.

Was ist ein eins-zu-eins-prozess?

Einfach ausgedrückt, ist eine eineindeutige oder injektive Funktion eine Funktion, bei der für zwei verschiedene \(x_1\) und \(x_2\) die Werte ihrer Bilder durch \(f(x)\) unterschiedlich sind, was mathematisch bedeutet

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

Manche Lehrkräfte schreiben es etwas anders, aber immer noch gleichwertig: Die Funktion ist eineindeutig, wenn

\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]

Dies bedeutet auf ziemlich raffinierte Weise, dass, wenn der Graph der Funktion denselben Wert (eine horizontale Linie) schneidet, dies nur geschieht, wenn der Punkt derselbe ist. Du sagst also nur, dass es keine zwei verschiedenen Punkte gibt, an denen eine horizontale Linie sie schneidet. Du wiederholst also nur die Horizontaler Linientest .

Wie prüft man, ob eine funktion eins-zu-eins ist oder nicht?

• Schritt 1: Beginnen Sie mit der ursprünglichen Funktion f(x), und setzen Sie die Gleichung y = f(x)
• Schritt 2: Versuch einer Lösung für x
• Schritt 3: Wenn Sie mehr als eine Lösung finden, ist die Funktion NICHT eineindeutig, und wenn sie eine Lösung oder keine Lösung hat, ist die Funktion eineindeutig

Normalerweise führen Sie eine grundlegende Prüfung durch, um sicherzustellen, dass diese Funktion eindeutig nicht eins-zu-eins ist, möglicherweise weil Sie leicht eine horizontale Linie finden können, die die HLT versagen lässt.

Dann werden Sie nach einigen grundlegenden visuellen Eigenschaften suchen: Ist die Funktion immer steigend (dann ist sie eineindeutig), und dasselbe gilt für den Fall, dass die Funktion immer fallend ist.

Wie hängt eins-zu-eins mit der suche nach dem kehrwert zusammen?

Einfach ausgedrückt: Um die Umkehrung einer Funktion zu finden, MUSS die Funktion eins zu eins sein, zumindest in einem bestimmten Teilbereich. Oftmals schränken wir den Bereich ein, so dass eine Funktion in einem eingeschränkten Bereich 1-zu-1 ist, was sie sonst nicht wäre.

Zum Beispiel ist \(f(x) = x^2\) insgesamt nicht eineindeutig. Warum, weil man zwei verschiedene Punkte \(x_1 = -1\) und \(x_2 = 1\) nehmen und feststellen kann, dass \(f(x_1) = (-1)^2 = 1\) und \(f(1) = 1^2 = 1\), was bedeutet, dass die Eigenschaft (die Eins-zu-Eins-Charakterisierung)

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

nicht erfüllt ist. Wenn wir nun statt der gesamten reellen Linie \(\R\) nur die positiven Werte betrachten, können wir schlussfolgern, dass die Funktion auf den positiven reellen Werten eins-zu-eins ist (Hinweis: Auf diesem Teilbereich ist die Funktion steigend)

Gibt es eine formel, um festzustellen, ob eine funktion eineindeutig ist?

Leider nicht. Ich meine, man könnte an \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \) als Eins-zu-Eins-Formel denken, aber das ist eher eine logische Bedingung als eine Formel.

Es gibt jedoch ein sehr allgemeines Verfahren, mit dem geprüft werden kann, ob eine Funktion eineindeutig ist oder nicht, und das ist das, was oben erklärt wird. Es gibt keine "Eins-zu-Eins-Formel". Wenn wir uns für eine entscheiden müssten, dann wäre es y = f(x).

Und dann lösen wir einfach für x. Nicht mehr und nicht weniger. Letztlich kommt es darauf an, worum es bei f(x) geht. Eine sehr komplexe, verschlungene Funktion kann sehr schwierig zu lösen sein, und vielleicht braucht man dafür einen Funktionsrechner, und selbst mit einem Funktionsrechner kann man scheitern.

Sie fragen sich wahrscheinlich, warum das so ist? Das liegt daran, dass wir im Grunde keine Techniken haben, um ALLE Gleichungen zu lösen. Wir tun nur, was wir können, wenn es um bestimmte Arten von Gleichungen geht, aber wir sind weit davon entfernt, eine EXAKTE Methode zur Lösung aller Gleichungen zu kennen.

Beispiel: eins-zu-eins-funktion

Ist die folgende Funktion injektiv? \(f(x) = \frac{1}{4} x + \frac{5}{4}\)

Lösung:

Die folgende Funktion wurde uns zur Verfügung gestellt:

\[f(x) = \frac{1}{4} x + \frac{5}{4}\]

Um festzustellen, ob die gegebene Funktion eineindeutig ist oder nicht, müssen wir \(x\) lösen und feststellen, ob es keine Lösung, eine Lösung oder mehrere Lösungen gibt. Die Ausgangsgleichung lautet

\[y=\frac{1}{4}x+\frac{5}{4}\]

Setzt man \(x\) auf die linke Seite und \(y\) und die Konstante auf die rechte Seite, erhält man

\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]

Löst man nun \(x\), indem man beide Seiten der Gleichung durch \(-\frac{1}{4}\) dividiert, erhält man folgendes

\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]

und vereinfachen wir endlich die folgenden

\[\displaystyle x=4y-5\]

Daher führt die Lösung von \(x\) für die gegebene lineare Gleichung zu \(x=4y-5\) und es gibt nur eine echte Lösung, so dass die gegebene Funktion eineindeutig ist.

Schlussfolgerung

Ausgehend von den Erkenntnissen des vorigen Abschnitts lässt sich schließen, dass die gegebene Funktion eineindeutig ist.

Grafisch:

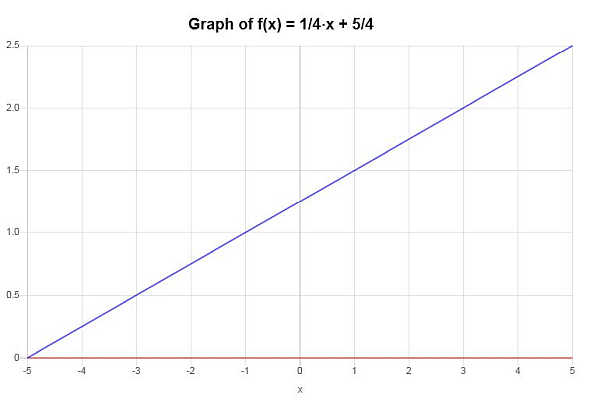
Beispiel: 1-zu-1-funktion

Beweisen oder widerlegen Sie, dass die folgende Funktion eineindeutig ist: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)

Lösung: Um festzustellen, ob die gegebene Funktion eineindeutig ist oder nicht, müssen wir \(x\) lösen und feststellen, ob es keine Lösung, eine Lösung oder mehrere Lösungen gibt. Die Ausgangsgleichung, die wir verwenden müssen, lautet:

\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]

Erstschritt: In diesem Fall müssen wir zunächst die gegebene Gleichung vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:

Die Lösungen lauten also:

\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]

Eins-zu-eins-status

Auf der Grundlage der oben gezeigten Arbeit kann gefolgert werden, dass die gegebene Funktion NICHT EINZIG ist, da sie den Horizontal Linientest nicht besteht, da zum Beispiel die Linie \(y = 0\) eine horizontale Linie ist, die die gegebene Funktion mehr als einmal kreuzt.

Grafisch lässt sich die Situation wie folgt darstellen:

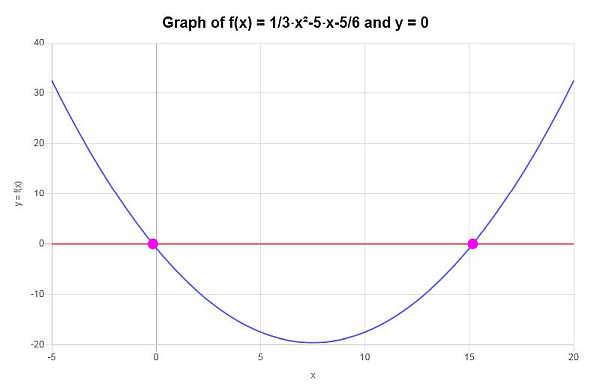
Weitere interessante algebra-rechner

Das Konzept der 1-zu-1-Funktionen wird in der Regel als selbstverständlich angesehen, aber es ist ein sehr wichtiges, ich würde sagen, ein kritisches Konzept. Denn das Konzept der Eins-zu-Eins-Funktionen ist eng mit der Idee der monotonen Funktion (zunehmende oder abnehmende Funktionen) verbunden, ebenso wie es eng mit dem Konzept der berechnung der Umkehrfunktion und sein Graph.

Dennoch ist es oft schwierig, den Wald vor lauter Bäumen nicht zu sehen, da die meisten wichtigen Konzepte der Algebra und der Infinitesimalrechnung eng miteinander verknüpft sind. Funktionsanalyse ist eines der Dinge, die Sie ständig tun werden, daher ist es gut, wenn Sie sich die Fähigkeiten aneignen, um darin gut zu werden.