Mehr über lineare funktionen

Mit diesem linearen Funktionsrechner können Sie a berechnen lineare Funkion durch Bereitstellung bestimmter erforderlicher Informationen über die Funktion.

Es gibt verschiedene Möglichkeiten, wie Sie dies tun können.Sie können entweder (1) eine lineare Gleichung in x und y liefern, die für y gelöst werden kann, oder (2) direkt die liefern Neigung und Y-Abschnitt , oder (3) Sie können die Steigung und einen Punkt angeben, an dem die Linie durchläuft, oder (4) Sie 2 Punkte angeben, an denen die Linie durchläuft.

Welche Informationen werden Sie bereitstellen?Es hängt weitgehend davon ab, welche Informationen Sie zur Verfügung haben, und hängt vom spezifischen Fall ab.

Ein häufiger Fall besteht darin, eine lineare Funktion zu finden, die zwei gegebene Punkte durchläuft, aber die anderen Möglichkeiten, die Linie zu bestimmen, sind ebenfalls häufig.

Was ist eine lineare funktion?

Die Antwort hängt davon ab, wie viele Variablen Sie in Betracht ziehen, aber für eine Variable x ist eine lineare Funktion eine Funktion des Formulars

\[f(x) = a + b x \]

Nur eine Technik, in fortgeschrittenerer Mathematik, ist dies eine lineare affine Funktion, und es ist nicht streng linear, es sei denn, A = 0, aber diese Idee geht über den Umfang dieser Präsentation hinaus.Für uns ist \(f(x) = a + b x \) eine lineare Funktion in x.

Der Wert von a in \(f(x) = a + b x \) ist als das bekannt Y-Abschnitt und b ist als die bekannt Neigung .Manchmal sehen Sie die Konvention \(f(x) = mx + n \), wobei m der Hang ist und n der y-Schnittpunkt ist.

Aber das ist eine Namenskonvention. Sie müssen sich nur daran erinnern, dass die Konstante, die die Variable X multipliziert, die Steigung ist und die andere die y-Schnittstelle ist.Warum das?Denn wenn x = 0, erhalten wir \(f(0) = m \cdot 0 + n = n\), was darauf hinweist, dass n genau das Warum -Abfang ist.

Was sind die schritte zum berechnen einer linearen funktion?

• Schritt 1: Identifizieren Sie, welche Art von Informationen Sie bereitgestellt haben
• Schritt 2: Wenn die Informationen, die Sie haben
• Schritt 3: Wenn Sie die Steigung B und den y-Intercept A haben, ist die lineare Funktion direkt f (x) = a + b x
• Schritt 5: Wenn Sie zwei Punkte haben.
• Schritt 6: Wenn Sie stattdessen einen Punkt haben \((x_1, y_1)\) wobei die Zeile durchgeht und die Steigung ist, können Sie die Formel verwenden: \(\displaystyle f(x) = y_1 + m(x-x_1)\) für die lineare Funktion

Die oben genannte Liste der Schritte ist eine umfassende Liste und berücksichtigt alle möglichen Fälle.Das ultimative, die einfachste und weniger beteiligte Situation entspricht dem Fall, in dem die Steigung und der Y-Grenzwert bekannt sind, wo wir das berechnen können Steigungsschnittform Sofort, aber das ist nicht immer der Fall.

Was ist die lineare funktionsformel

Letztendlich und unabhängig von den Informationen, die Sie zur Verfügung gestellt haben, können Sie zur linearen Funktionsformel gelangen, die als Neigungsformular bezeichnet wird, nämlich:

\[y = a + bx \]

Da Sie nun eine Funktion definieren, können Sie auch \(f(x) = a + b x\) schreiben.

Was sind die schritte, um die lineare funktionsformel zu finden?

• Schritt 1: Identifizieren Sie die bereitgestellten Informationen
• Schritt 2: Erreichen
• Schritt 3: Ersetzen Sie y durch f (x) und schreiben Sie f (x) = a + bx

Geometrisch die Lineare Funktion Grafik wird eine Linie sein, die die y-Achse am Punkt (0, a) tatsächlich überschreitet, und die Steigung B spiegelt den Grad der Neigung der Linie wider.

Warum ist es nützlich, lineare funktionen zu berechnen?

Die lineare Beziehung zwischen Variablen ist in so vielen Anwendungen sehr häufig. Daher wird es unverzichtbar zu verstehen, wie lineare Funktionen funktionieren.

Und wir können auch lineare Funktionen für mehr Variablen definieren, die sie zu einem noch leistungsfähigeren Objekt machen.

Beispiel: linearer funktionsrechner

Berechnen Sie die Gleichung der linearen Funktion, die durch die Punkte fließt: \( (\frac{22}{3}, \frac{7}{4})\) und \((-1, \frac{5}{6})\)

Lösung: Das Hauptziel besteht darin, eine lineare Funktion basierend auf den bereitgestellten Informationen nach Möglichkeit zu konstruieren.

Die Informationen zur Linie sind, dass die Zeile durch die Punkte \(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\) und \(\displaystyle \left( -1, \frac{5}{6}\right)\) geleitet wird

Daher besteht der erste Schritt bei der Berechnung der Steigung.Die Formel für die Steigung lautet: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Wenn wir nonne die Inprechenden Zahlen Anschlieben, Erhalten Wir, Dass Die Steigung: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{5}{6} - \frac{7}{4}}{ \displaystyle -1 - \frac{22}{3}} = \frac{ \displaystyle \frac{5}{6}-\frac{7}{4}}{ \displaystyle -1-\frac{22}{3}} = \frac{11}{100}\] Ist

Dann Wissen Wire, Dass sterg steigung \(\displaystyle m = \frac{11}{100}\) ist und Dass die Linie -durchs -punkt -verlauf \(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\)

DAHER KRNNEN WIR MIT DEN INFORMATIONEN, DIE WIR HABEN, DIREKT DIE PUNKT-SLOPE-FORM DER LINIE Konstrieren, Die ist Ist

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

und dann Die Bekannten Werte von << xyz >> und << xyz >> Anschlieben, Wir Bekommen Das

\[\displaystyle y-\frac{7}{4} = \frac{11}{100} \left(x-\frac{22}{3}\right)\]

Jetzt Müssen Wir Sterbe Site der Gleisung Erweitern, Indem Wir der Steigung Verteiil, Damit Wir \[\displaystyle y = \frac{11}{100} x + \frac{11}{100} \left(-\frac{22}{3}\right) + \frac{7}{4}\] Erhalten

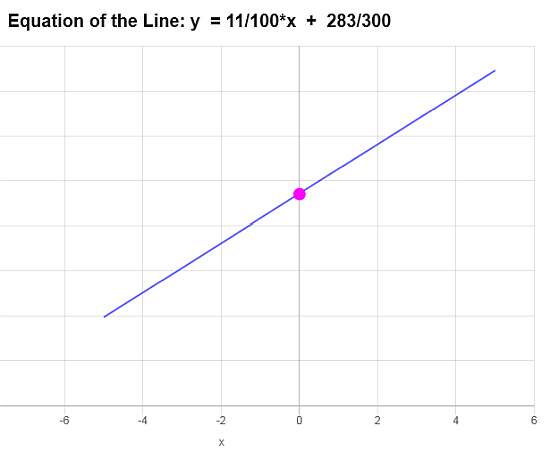
und Vereinfachen Wir des \[\displaystyle y=\frac{11}{100}x+\frac{283}{300}\]

Fazit : Basierend auf dem Bereitgestellten DATEN SCHLIEBEN WIR, Dass Die Gleisung der Zeilung \(\displaystyle f(x)=\frac{11}{100}x+\frac{283}{300}\) ist und Einer Zeille MIT Einer Steigung von \(\displaystyle b = \frac{11}{100}\) und y-Sschnittstelle von \(\displaystyle a = \frac{283}{300}\) eentShritz.

Basierend Auf Diesen Informationne Lautet Die Grafik:

Wasspiel: eine andere berechnung der linearen funksfunkion

Berechnen Sie Die lineare Funktion Zugeordnet MIT: \(\frac{1}{3}x + \frac{5}{4}y - \frac{5}{6} = 0\)

Lösung:

In Dieem BEISPIEL HABEN WIR NUN EINE LINEARE FUNKTION HUBER EINE Aulein Lineare Geilung Delatelert, Die Kachen:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Wirkkkön Können Konstanten Vereinfachen:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Nick

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Vermsen Sie Nun fürs;

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{5}{6}}{\frac{5}{4}}\]

und Vereinfachen Verendlich Sterben Folgenden

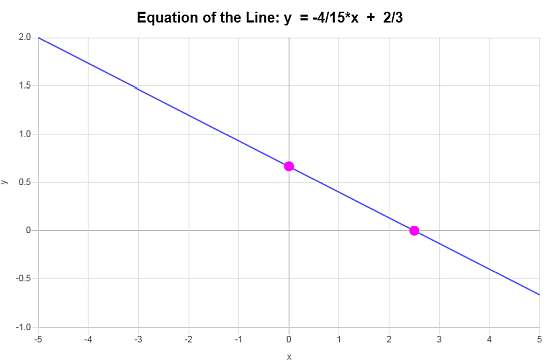
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{3}\]

Fazit >.

Basierend Auf Diesen Informationne Lautet Die Grafik:

Beisiziel: lineare funkionsrechtner

Berechnen Sie Die lineare Funktion MIT Steigung M = 0 und Das überschreiitet Die y-achse am punkt (0, 4).

Lösung: In Diesim Fall Haven Wir stergarung Gegeben, Die M = 0 IST, und Den y-Sschnittpunkt, Das ist (0, 4) .Da Stergarung 0 Ist, ist die linie horizontal, auch in Dieem Herbst Sterben Die Gleichung der Linie << istxyza>>.

Lineare funkionsrechtner

Interessante Taschenrechner Sind der Steigungsrechner und Den y-Grenzütahme-rechner. Fondse der Senkrrecht Linie Zuur Bester Linie .

Ein weitere Gemeinsame Form für die Linie ist Sterben Standardform , und sie Könsnen Bestmt von Einer Form in Derere Konvertieren.