Mehr über die formel des hangs

Dies Hangformel Durch den Rechner können Sie die Steigung für zwei angegebene Punkte des Formulars (x, y) unter Verwendung der bekannten Formel verwenden, die alle Schritte zeigt.

Sie müssen zwei Punkte des Formulars (x, y) angeben.Sie können beispielsweise Punkte wie (1/2, 1/3) oder etwas angeben, das nicht vereinfacht wird wie (1/3+1/4, SQRT (8)).

Sobald Sie zwei gültige Punkte des Formulars (x, y) angegeben haben, werden Sie im nächsten Schritt auf die Schaltfläche "Berechnen" klicken, und Sie erhalten alle Schritte der Steigungsformelberechnungen.

Das Konzept der Steigung ist entscheidend in Algebra und Geometrie, und die Steigung ist sehr wichtig für die Konstruktion von a lineare Funkion .

Was ist die formel des hangs?

Angenommen, wir haben zwei Punkte \((x_1, y_1)\) und \((x_2, y_2)\) im Flugzeug.Dann ist die Formel Des hängt ist :

\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]

Einige Leute werden sagen: "Es ist das Verhältnis zwischen dem Unterschied in Ys und dem Unterschied in X", mit der Einschränkung, dass Sie die Reihenfolge bei den Unterschieden bewahren müssen.Wenn Sie oben \(y_2 - y_1\) tun, dann tun Sie unten \(x_2 - x_1\) und nicht \(x_1 - x_2\).

Einige Leute nennen diese Steigungsformel "Aufstieg gegen Run"//

Was sind die schritte für die verwendung der formel der steigung?

• Schritt 1: Identifizieren Sie die beiden angegebenen Punkte.Es ist eine gute Idee, die Ausdrücke so weit wie möglich zu vereinfachen, bevor die Formel verwendet wird
• Schritt 2: Bestimmen Sie, welcher der erste Punkt ist und was der zweite ist.Die Wahl ist für das Ergebnis irrelevant, vorausgesetzt, Sie bleiben mit Ihrer Wahl überein
• Schritt 3: Verwenden Sie die Formel \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\) Durch Einstecken der Werte des ersten Punktes \(x_1\) und \(y_1\) und des zweiten Punkts \(x_2\) und \(y_2\)
• Schritt 4: Vereinfachen Sie nach dem Einstecken der Werte so weit wie möglich, um die Steigung auf die einfachste Form zu reduzieren

Die Berechnung der Steigung unter Verwendung der Formel ist normalerweise ein sehr einfacher Prozess. Halten Sie einfach die Reihenfolge der Punkte konsistent.

Wie benutze ich den hang?

Die Steigung ist ein Maß für die Neigung einer Linie.In der Tat, wenn Sie eine lineare Funktion der Form haben

\[y = m x + n\]

Dann ist die Steigung der Linie m.Das obige ist als das bekannt Steigungsschnittform einer Linie.

Was sind die schritte für die verwendung der steigung für eine linie?

• Schritt 1: Identifizieren Sie die Steigung m.Vereinfachen Sie es so weit wie möglich
• Schritt 2: Sie müssen den y-Schnittpunkt kennen, dies ist der Punkt in der y-Achse, wenn die Linie ihn überschreitet, und nennen Sie es n
• Schritt 3: Dann ist die Gleichung der Zeile \(y = m x + n\)

Es gibt andere Formen, die die Linie anders ausdrücken als die Hangabschnitt .Du hast die Standardform der Linie , und die Point-Slope-Form .

So verwenden sie die formel zur steigungsschnittschnittstelle

Das ist das Zentrum von Lineare Funktionen (oder linear affine wir sollten sagen) und lineare Graphen.Wenn Sie die Steigung m und den y-Schnittpunkt N haben, berechnen Sie die Gleichung der Linie direkt als y = mx + n.

Geometrisch ist das ziemlich einfach zu interpretieren, da der y-Schnittpunkt absolut klar ist, da der Schnittpunkt zwischen der Linie und der Y-Achse, und die Steigung ist das Maß für die Neigung.Als Referenz entspricht eine Steigung von m = 1 einer Neigung von 45 ^Ö .

Umgekehrt, wenn Sie welche haben lineare Funkion , durch Algebrasche Vereinfachung Sie können jederzeit auf die Steigungsschnittform y = mx + n reduzieren, und dann haben Sie Ihre Steigung m und y-Intercept n gefunden.

Beispiel: verwenden der formel der steigung

Berechnen Sie die Steigung für die folgenden Punkte: \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) und \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)

Lösung: Wir müssen die Steigung einer Linie berechnen, die durch die Punkte \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) und \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) fließt.

Die folgende Formel ist erforderlich, um die Steigung angesichts der beiden Punkte zu berechnen:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Stecken Sie nun die Werte der Punkte \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) und \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) führt zu:

Daher schließen wir, dass die Neigung einer Zeile, die die Punkte durchgeht \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) und \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) ist \(m = \displaystyle \frac{1}{4}\).

Beispiel: weitere beispiele für die steigungsformel

Verwenden Sie die Steigungsformel, um die Steigung der Linie zu finden, die durch die Punkte geht: \((2, 4)\) und \((5, 12)\)

Lösung: In diesem Fall haben wir die Punkte \(\displaystyle (x_1, y_1) = \left(2,4\right)\) und \(\displaystyle (x_2, y_2) = \left(5,12\right)\), die die Punkte sind, von denen wir wissen, dass sie die Linie durchlaufen.

Die Steigungsformel lautet:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Stecken Sie nun die Werte der Punkte \(\displaystyle (x_1, y_1) = \left(2,4\right)\) und \(\displaystyle (x_2, y_2) = \left(5,12\right)\) führt zu:

Daher schließen wir, dass die Neigung einer Zeile, die die Punkte durchgeht \(\displaystyle (x_1, y_1) = \left(2,4\right)\) und \(\displaystyle (x_2, y_2) = \left(5,12\right)\) ist \(m = \displaystyle \frac{8}{3}\).

Beispiel: slope-außenschnittformular

Finden Sie die Slope Intercept -Form für die folgende Zeile: \(2x + 4y = 3 + \frac{1}{2}x\).

Lösung: Wir haben die folgende Gleichung:

\[\displaystyle 2x+4y=3+\frac{1}{2}x\]

Puting \(y\) auf der linken Seite und \(x\) und die Konstante auf der rechten Seite bekommen wir

\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]

Jetzt ist der Begriff \(y\) \( 4 - 0 = 4\) und auch da \( \frac{1}{2} - 2 = -\frac{3}{2}\) wird Folgendes erhalten

\[\displaystyle 4y=-\frac{3}{2}x+3\]

Wenn Sie nun für \(y\) gelöst werden, indem beide Seiten der Gleichung durch \(4\) geteilt werden, wird Folgendes erhalten

\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]

und vereinfachen wir endlich die folgenden

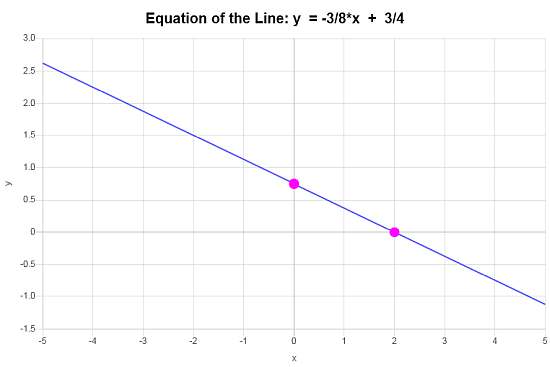
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]

Fazit : Basierend auf den bereitgestellten Daten schließen wir, dass die Gleichung der Linie im Steigungsschnittschnitt \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\) mit einer Steigung von \(\displaystyle b = -\frac{3}{8}\) und y-Schnittstelle von \(\displaystyle n = \frac{3}{4}\) ist.

Grafisch sieht die Linie aus wie:

Andere lineare funktionsrechner

Zusammen mit quadratische funktionen Lineare Funktionen gehören zu den wichtigsten Objekten in der Mathematik.Sie können die Steigung einer Linie berechnen, die finden Senkrecht Linie und konvertieren die Linie je nach Bedarf zwischen verschiedenen Formen.

Eine Sache, die für lineare Funktionen bemerkenswert ist, ist, dass es einfacher zu finden ist inverse lineare Funktionen wie die meisten linearen Funktionen 1-zu-1 sind (mit Ausnahme horizontaler Linien).