Leitungspunkt-Slope-Formularrechner
Anweisungen: Verwenden Sie diesen Taschenrechner, um die Form der Steigungsschnittstelle der von Ihnen bereitgestellten Linie zu ermitteln, wobei alle Schritte angezeigt werden.Zu diesem Zweck müssen Sie einige Informationen über die Zeile geben, die Sie in Point-Slope-Form einstellen möchten.
Es gibt verschiedene Möglichkeiten, wie Sie uns über Ihre Linie informieren können.Sie können: (1) Sowohl die Steigung als auch die Y-Schnittstelle, (2) Sie können jede lineare Gleichung eingeben (z.Durchgeht oder (4) Sie können zwei Punkte angeben, an denen die Linie durchgeht.
Über diesen Punkt-Slope-Formrechner der Linie.
Dieser Point-Slope-Gleichungsrechner bietet Ihnen eine Schritt-für-Schritt-Berechnung der Gleichung der Linie in der Punkt-Slope-Form für jede von Ihnen ursprünglich bereitgestellte Linie.
Sie müssen die Linie identifizieren, mit der Sie arbeiten möchten.Diese Zeile kann in vielen verschiedenen identifiziert werden, und Sie werden basierend auf den von Ihnen bereitgestellten Informationen auswählen.
Eine der häufigsten Möglichkeiten ist es, eine Linie zu definieren, indem sie ihren Hang und ihre anbietet Y-abschnitt , aber es ist sicherlich nicht der einzige Weg.
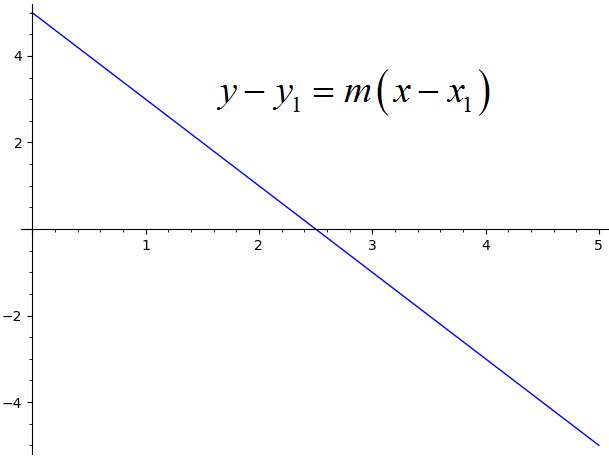
Wie stellt man eine Linie in Point-Slope-Form dar?
Eine Zeile soll in Punkt-Slope-Form sein, wenn sie geschrieben werden kann wie:
\[y - y_1= m (x -x_1)\]In diesem Zusammenhang wird \(m\) als Steigung der Zeile identifiziert, und \((x_1, y_1)\) ist ein Punkt, durch den die Linie durchgeht.
Wie können Sie den Punktschnittschnittstellen mit einem Taschenrechner finden?
Wenn Sie die Steigung \(m\) der Linie und einen Punkt \((x_1, y_1)\) kennenvon Informationen.
Warum ist die Point-Slope-Form einer Linie nützlich?
Die Point-Slope-Form ist nützlich, da sie als direkte Interpretation des Hänge der Linie als Änderungsrate.In der Tat direkt aus dem Punkt-Slope-Formular bekommen wir
\[\frac{y-y_1}{x-x_1} = m\]Kann ich mit zwei Punkten eine Punktneigungform erhalten?
Ja!Wenn Sie zwei Punkte haben, verwenden Sie sie zuerst, um die Steigung \(m\) zu berechnen und die Punkte auszuwählen, um die Formel direkt anzuwenden
\[y - y_1= m (x -x_1)\]
Beispiel: Point-Slope Form-Berechnung
Angenommen, Sie wissen, dass die Linie durch die Punkte geht \(( \frac{1}{3}, 2)\) und \((\frac{7}{2}, 3)\).Finden Sie die Punkt-Slope-Form der Linie.
Antworten:
Die Informationen zur Linie sind, dass die Zeile durch die Punkte \(\displaystyle \left( \frac{1}{3}, 2\right)\) und \(\displaystyle \left( \frac{7}{2}, 3\right)\) geleitet wird
Daher besteht der erste Schritt bei der Berechnung der Steigung.Die Formel für die Steigung lautet: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]
Wenn wir nonne die Inprechenden Zahlen Anschlieben, Erhalten Wir, Dass Die Steigung: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 3 - 2}{ \displaystyle \frac{7}{2} - \frac{1}{3}} = \frac{ \displaystyle 1}{ \displaystyle \frac{19}{6}} = \frac{6}{19}\] Ist
Dann Wissen Wire, Dass sterg steigung \(\displaystyle m = \frac{6}{19}\) ist und Dass die Linie -durchs -punkt -verlauf \(\displaystyle \left( \frac{1}{3}, 2\right)\)
DAHER KRNNEN WIR MIT DEN INFORMATIONEN, DIE WIR HABEN, DIREKT DIE PUNKT-SLOPE-FORM DER LINIE Konstrieren, Die ist Ist
\[\displaystyle y - y_1 = m \left(x - x_1\right)\]und dann Die Bekannten Werte von << xyz >> und << xyz >> Anschlieben, Wir Bekommen Das
\[\displaystyle y-2 = \frac{6}{19} \left(x-\frac{1}{3}\right)\]Fazit : Basisend auf Den Bereitgestellten DATEN Schliebe Wir, Dass Die Geilung der Linie im Punkt-Slope-Form \(\displaystyle y-2=\frac{6}{19}\left(x-\frac{1}{3}\right) \) ist.
Sie Könsnen und Unere Verwenden StandardformularStrechner und Hang-Intercept-Rechner Ine Stirbt Stattdessen Sterat Sindate Sind, Ein Denen siieder -ind.




