So verwenden sie diesen neigungsrechner mit schritten

Verwenden Sie diesen Taschenrechner, um die Steigung einer von Ihnen bereitgestellten Zeile zu ermitteln, wobei alle Schritte angezeigt werden.

Die Steigung ist ein Maß für die Neigung der Linie in Bezug auf die koordinierten Achsen.Eine positive Steigung zeigt an, dass die Linie eine Aufwärtsneigung aufweist, während eine negative Steigung angibt, dass die Linie eine Abwärtsneigung aufweist.

Eine Steigung von Null zeigt an, dass die Linie horizonal ist, während eine vertikale Linie keine gut definierte Steigung hat.

Wie berechnet man eine steigung?

Normalerweise ist die Berechnung der Steigung einfach, aber es gibt mehrere Möglichkeiten, eine Steigung zu berechnen, und es hängt alles davon ab, welche Informationen bereitgestellt werden und wie sie bereitgestellt werden.

Am häufigsten wird eine Steigungsberechnung präsentiert, indem man Ihnen zunächst eine lineare Gleichung vorgibt, für die Sie die Steigung finden müssen, oder wenn man Ihnen zwei Punkte vorgibt, durch die eine Linie verläuft.

Steigrechner aus gleichung: finden der steigung der linie

Dieser Taschenrechner zeigt Ihnen, wie Sie die Steigung einer von Ihnen bereitgestellten Zeile berechnen können, und Sie haben unterschiedliche Möglichkeiten, Ihre Linie anzuzeigen und zu definieren.Es gibt Ihnen auch ein Diagramm, das die berechnete Steigung widerspiegelt.

Beispielsweise besteht eine häufige Möglichkeit darin, Ihre Linie zu definieren, die eine Gleichung angibt, und dann haben Sie diesen Taschenrechner, um die Steigung aus der Gleichung zu berechnen.

Die allgemeine Strategie dafür ist zu Lenzend sie Die Geilung der Linie in Steigabschnittform ein , woraus sich die Steigung aus der Struktur der Gleichung \(y = mx + n\) leicht erkennen lässt.

Dies ist auch eine steigung von zwei punktenrechner

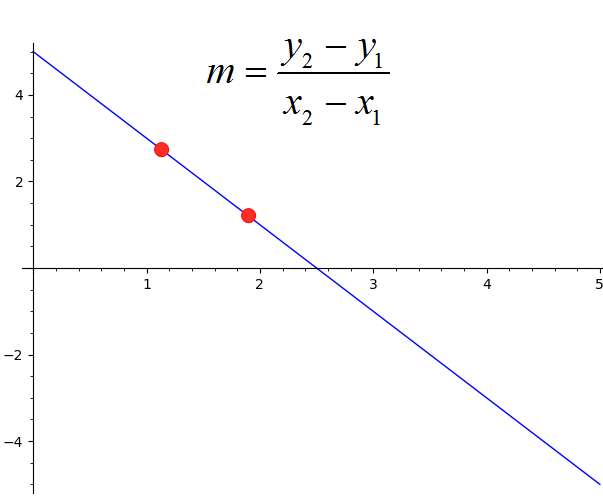
Vielleicht ist eine der häufigsten Möglichkeiten, die Steigung zu berechnen, wenn Sie Definiere sie Die Gleisung, Indem Sie Zwei Punkte Bereitstellen als \((x_1, y_1)\), \((x_2, y_2)\). Wie findet man nun die Steigung aus zwei Punkten? Die Steigung wird einfach wie folgt berechnet

\[m = \frac{y_2-y_1}{x_2-x_1}\]

So findet man den Hang aus zwei Punkten.Vergessen wir nicht, dass diese beiden Punkte normalerweise Punkte sind, an denen eine Linie durchläuft, sodass Sie die Steigung der Linie finden, die diese Punkte durchläuft.

Letztendlich hängt das Finden der Steigung einer Linie davon ab, wie die Linie definiert ist.Mit diesem Rechner werden Sie mit allen Fällen bedeckt, auch wenn in der Berechnung Fraktionen vorhanden sind.

Interpretation: was ist eine steigung von 2%?

Es gibt mehrere Möglichkeiten, dies zu sehen, aber eine gängige ist, dass für jeden Anstieg um 100 Einheiten in X die Linie um 2 Einheiten in Y ansteigt, was die 2/100 = 0,02 = 2 % erklärt.

Nach dem gleichen Prinzip kann man sagen, dass eine Steigung von 45 % bedeutet, dass ein Anstieg von X um 100 Einheiten zu einem Anstieg von Y um 45 Einheiten führt. Bitte beachten Sie, dass dies NICHT dasselbe ist wie eine Steigung von 45 ^o grades.

Sofortiger neigungsrechner

Die Idee eines Steigungsrechners ist einfach, wenn Sie zwei Punkte berücksichtigen. In diesem Fall verwenden Sie die obige Formel.Aber was ist der sofortige Hang?Das bezieht sich auf die Neigung, wenn die beiden Punkte nahe kommen.

Sie möchten also sehen, welcher Wert sich der Steigung nähert, wenn sich die beiden Punkte gemeinsam nähern.Die Idee der sofortigen Steigung spiegelt sich dabei wider Derivatnetisch , was im Wesentlichen sofortige Hänge berechnet.

Beispiel: berechnung der steigung

Angenommen, Sie haben eine Linie, die die folgende Standardform \( \frac{3}{4} x + 2y = 6\) hat. Ermitteln Sie die Steigung der Geraden.

Lösung: Berechnung der Steigung einer Linie

Wir Wurden mit der Folgenden Gleisung Versehen:

#XYZA

Setzt man \(y\) auf die linke Seite und \(x\) und die Konstante auf die rechte Seite, erhält man

#XYZA

Löst man nun \(y\), indem man beide Seiten der Gleichung durch \(2\) dividiert, erhält man folgendes

#XYZA

und Vereinfachen Verendlich Sterben Folgenden

#XYZA

Schlussfolgerung : Auf der Grundlage der angegebenen Daten schließen wir, dass die Steigung der Linie \(\displaystyle m = -\frac{3}{8}\) ist.

Wasspiel: berechnung der steigung von zwei punkten

Angenommen, Sie haben eine Linie, die durch 2 Punkte verläuft: \( (1, 2)\) und \( (4, 11/3)\). Finden Sie die Steigung der Linie.

Lösung:

Berechnung der steigung einer linie

Die Information über die Linie ist, dass die Linie durch die Punkte \(\displaystyle \left( 1, 2\right)\) und \(\displaystyle \left( 4, \frac{11}{3}\right)\) verläuft

Der erste Schritt besteht also darin, die Steigung zu berechnen. Die Formel für die Steigung lautet: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]

Setzt man nun die entsprechenden Zahlen mit ist ein, so ergibt sich die Steigung: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{11}{3} - 2}{ \displaystyle 4 - 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]

Wir stellen also fest, dass die Steigung \(\displaystyle m = \frac{5}{9}\) ist und dass die Linie durch den Punkt \(\displaystyle \left( 1, 2\right)\) verläuft

Schlussfolgerung : Auf der Grundlage der angegebenen Daten schließen wir, dass die Steigung der Linie \(\displaystyle m = \frac{5}{9}\) ist.

Die Neigung Einer Linie ist Y-Abschnitt und x-schnittstelle , Weil Sie im WesentLichen Sterben Linie Definierter.