Más sobre la fórmula de la pendiente

Este Fórmula de pendiente La calculadora te permitirá calcular la pendiente de dos puntos dados de la forma (x, y) usando la conocida fórmula, mostrando todos los pasos.

Debe proporcionar dos puntos de la forma (x, y). Por ejemplo, puede proporcionar puntos como (1/2, 1/3) o algo que no esté simplificado como (1/3+1/4, sqrt(8)).

Una vez que proporcione dos puntos válidos de la forma (x, y), el siguiente paso es hacer clic en el botón que dice "Calcular", y se le proporcionarán todos los pasos de los cálculos de la fórmula de la pendiente.

El concepto de pendiente es crucial en Álgebra y Geometría, y la pendiente es muy importante para la construcción de un función lineal .

¿cuál es la fórmula de la pendiente?

Supongamos que tenemos dos puntos \((x_1, y_1)\) y \((x_2, y_2)\) en el plano. Entonces el fórmula de la pendiente es :

\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]

Algunas personas dirán "es la relación entre la diferencia en y y la diferencia en x", con la advertencia de que debe conservar el orden al hacer las diferencias. Si arriba haces \(y_2 - y_1\), entonces abajo haces \(x_2 - x_1\) y no \(x_1 - x_2\).

Además, algunas personas llaman a esta fórmula de pendiente "Rise versus Run"/

¿cuáles son los pasos para usar la fórmula de la pendiente?

• Paso 1: Identifique los dos puntos dados. Es una buena idea simplificar las expresiones tanto como sea posible, antes de usar la fórmula
• Paso 2: Determina cuál es el primer punto, y cuál el segundo. La elección es irrelevante para el resultado, siempre que sea coherente con su elección.
• Paso 3: Usa la fórmula \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\) reemplazando los valores del primer punto \(x_1\) y \(y_1\), y del segundo punto \(x_2\) y \(y_2\)
• Paso 4: Después de ingresar los valores, simplifique tanto como sea posible, para reducir la pendiente a su forma más simple

El cálculo de la pendiente usando la fórmula suele ser un proceso muy simple, solo asegúrese de mantener constante el orden de los puntos.

¿cómo usar la pendiente?

La pendiente es una medida de la inclinación de una recta. De hecho, cuando tienes una función lineal de la forma

\[y = m x + n\]

entonces, la pendiente de la recta es m. Lo anterior se conoce como el forma de intersección de pendientes de una linea

¿cuáles son los pasos para usar la pendiente de una línea?

• Paso 1: Identifica la pendiente m. Simplificarlo tanto como sea posible.
• Paso 2: Necesitas conocer el intercepto en y, esto es, el punto en el eje y cuando la línea lo cruza, y llámalo n
• Paso 3: Entonces, la ecuación de la recta es \(y = m x + n\)

Hay otras formas de expresar la línea además de la Intersección de la pendiente . Tienes el forma estándar de la línea , y el Forma punto-pendiente .

Cómo usar la fórmula pendiente-intersección

Ese es el centro de funciones lineales (o afines lineales deberíamos decir) y grafos lineales. De hecho, cuando tienes la pendiente m y el intercepto en y n, calculas directamente la ecuación de la línea como y = mx + n.

Geométricamente, eso es bastante simple de interpretar, ya que la intersección y es absolutamente clara como el punto de intersección entre la línea y el eje y, y la pendiente es la medida de la inclinación. Como referencia, una pendiente de m = 1 corresponde a una inclinación de 45 ^o .

Por el contrario, si tiene alguna función lineal , a través de Simplificación Algebraica siempre puedes reducir a la forma pendiente-intersección y = mx + n, y entonces habrás encontrado tu pendiente m y la intersección en y n.

Ejemplo: usar la fórmula de la pendiente

Calcular la pendiente para los siguientes puntos: \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) y \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)

Solución: Necesitamos calcular la pendiente de una recta que pasa por los puntos \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) y \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\).

Se necesita la siguiente fórmula para calcular la pendiente dados los dos puntos:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Ahora, reemplazando los valores de los puntos \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) y \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) conduce a:

Por tanto, concluimos que la pendiente de una recta que pasa por los puntos \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) y \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) es \(m = \displaystyle \frac{1}{4}\).

Ejemplo: más ejemplos de la fórmula de la pendiente

Usa la fórmula de la pendiente para encontrar la pendiente de la línea que pasa por los puntos: \((2, 4)\) y \((5, 12)\)

Solución: En este caso tenemos los puntos \(\displaystyle (x_1, y_1) = \left(2,4\right)\) y \(\displaystyle (x_2, y_2) = \left(5,12\right)\), que son los puntos por los que sabemos que pasa la recta.

La fórmula de la pendiente es:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Ahora, reemplazando los valores de los puntos \(\displaystyle (x_1, y_1) = \left(2,4\right)\) y \(\displaystyle (x_2, y_2) = \left(5,12\right)\) conduce a:

Por tanto, concluimos que la pendiente de una recta que pasa por los puntos \(\displaystyle (x_1, y_1) = \left(2,4\right)\) y \(\displaystyle (x_2, y_2) = \left(5,12\right)\) es \(m = \displaystyle \frac{8}{3}\).

Ejemplo: forma pendiente-intersección

Encuentra la forma de intersección de la pendiente para la siguiente línea: \(2x + 4y = 3 + \frac{1}{2}x\).

Solución: Tenemos la siguiente ecuación:

\[\displaystyle 2x+4y=3+\frac{1}{2}x\]

Poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]

Ahora bien, el término multiplicando \(y\) es \( 4 - 0 = 4\), y además desde \( \frac{1}{2} - 2 = -\frac{3}{2}\), se obtiene lo siguiente

\[\displaystyle 4y=-\frac{3}{2}x+3\]

Ahora, resolviendo para \(y\), dividiendo ambos lados de la ecuación por \(4\), se obtiene lo siguiente

\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]

y simplificando obtenemos finalmente lo siguiente

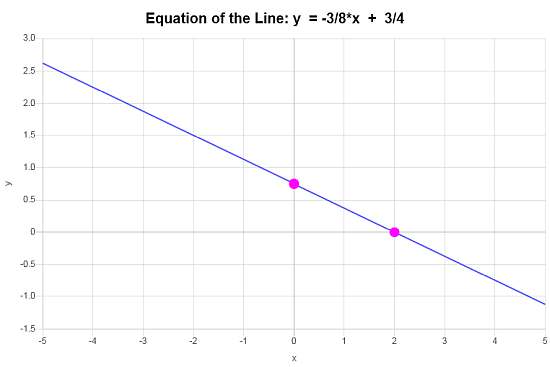
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]

Conclusión : Con base en los datos proporcionados, concluimos que la ecuación de la línea en forma de pendiente-intersección es \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\), con una pendiente de \(\displaystyle b = -\frac{3}{8}\) y una intersección en y de \(\displaystyle n = \frac{3}{4}\).

Gráficamente, la línea se ve así:

Otras calculadoras de funciones lineales

Juntos con funciones cuadráticas , las funciones lineales se encuentran entre los objetos más importantes en matemáticas. puedes calcular la pendiente de una línea, encontrar la perpendicular line , y convertir la línea entre diferentes formas, dependiendo de las necesidades.

Una cosa que es notable para las funciones lineales es que es más fácil encontrar funciones lineales inversas , ya que la mayoría de las funciones lineales son 1 a 1 (excepto las líneas horizontales).