Cómo utilizar esta calculadora de pendientes con pasos

Utiliza esta calculadora para hallar la pendiente de una recta que proporciones, con todos los pasos que se muestran.

La pendiente es una medida de la inclinación de la línea con respecto a los ejes coordenados. Una pendiente positiva indica que la línea tiene una inclinación ascendente, mientras que una pendiente negativa indica que la línea tiene una inclinación descendente.

Una pendiente igual a cero indica que la línea es horizontal, mientras que una línea vertical no tiene una pendiente bien definida.

¿cómo calcular una pendiente?

Normalmente el cálculo de la pendiente es fácil, pero hay varias formas de calcularla y todo depende de qué información se proporciona y cómo se proporciona.

Las formas más comunes en que se presenta un cálculo de pendiente es proporcionándole primero una ecuación lineal para la cual necesita encontrar su pendiente, o cuando le brindan dos puntos por los que pasa una línea.

Calculadora de pendiente a partir de la ecuación: encontrar la pendiente de la línea

Esta calculadora le mostrará cómo calcular la pendiente de una línea que proporcione, y tendrá diferentes formas de indicar y definir su línea. También le dará un gráfico que refleja la pendiente calculada.

Por ejemplo, una forma común es definir tu línea dando una ecuación, y luego tendrás esta calculadora para calcular la pendiente a partir de la ecuación.

La estrategia general para ello es poner la ecuación de la recta en forma de pendiente-intercepto , desde cuyo punto es fácil reconocer la pendiente a partir de la estructura de la ecuación \(y = mx + n\).

Esta es una calculadora de pendiente de dos puntos también

Quizás una de las formas más comunes de calcular la pendiente es cuando definir la ecuación proporcionando dos puntos como \((x_1, y_1)\), \((x_2, y_2)\). Entonces, ¿cómo encuentras la pendiente desde dos puntos? La pendiente se calcula simplemente como

\[m = \frac{y_2-y_1}{x_2-x_1}\]

que es como hallar la pendiente de dos puntos. No olvidemos que esos dos puntos suelen ser puntos por donde pasa una línea, por lo que estás encontrando la pendiente de la línea que pasa por esos puntos.

En definitiva, la forma de hallar la pendiente de una recta dependerá de cómo esté definida la recta. Esta calculadora te cubrirá todos los casos, incluso cuando haya fracciones en el cálculo.

Interpretación: ¿qué es una pendiente del 2%?

Hay varias formas de ver esto, pero una forma común es pensar que por cada aumento de 100 unidades en X, la recta aumenta 2 unidades en Y, lo que explica el 2/100 = 0,02 = 2%.

En la misma línea de interpretación, se puede decir que una pendiente del 45% es tal que un aumento de 100 unidades en X conduce a un aumento de 45 unidades en Y. Tenga en cuenta que esto NO es lo mismo que una pendiente con 45 ^O grados.

Calculadora de pendiente instantánea

La idea de una calculadora de pendientes es simple cuando consideras dos puntos, en cuyo caso usas la fórmula anterior. Pero, ¿cuál es la pendiente instantánea? Eso se refiere a la pendiente cuando los dos puntos se acercan cada vez más.

Entonces, también desea ver a qué valor se acerca la pendiente, cuando los dos puntos se acercan juntos. La idea de la pendiente instantánea se refleja en esta calculadora de derivadas , que básicamente calcula pendientes instantáneas.

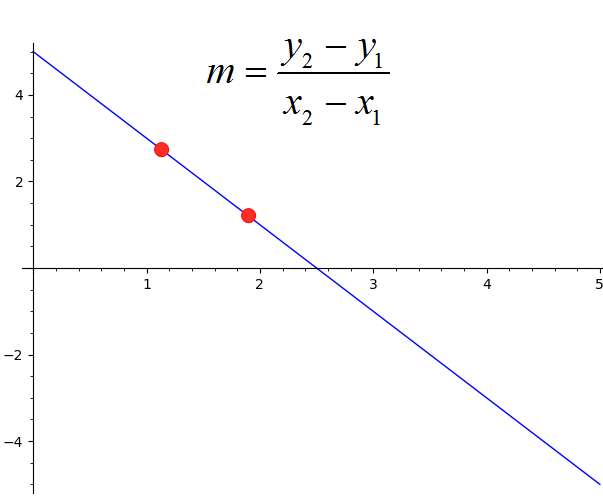
Ejemplo: cálculo de la pendiente

Suponga que tiene una línea que tiene el siguiente formato estándar \( \frac{3}{4} x + 2y = 6\). Encuentra la pendiente de la recta.

Solución: Cálculo de la pendiente de una línea

Nos han proporcionado la siguiente ecuación:

\[\displaystyle \frac{3}{4}x+2y=6\]

Poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle 2y = -\frac{3}{4}x +6\]

Ahora, resolviendo \(y\), al dividir ambos lados de la ecuación entre \(2\), se obtiene lo siguiente

\[\displaystyle y=-\frac{\frac{3}{4}}{2}x+\frac{6}{2}\]

y simplificando obtenemos finalmente lo siguiente

\[\displaystyle y=-\frac{3}{8}x+3\]

Conclusión : Con base en los datos proporcionados, concluimos que la pendiente de la recta es \(\displaystyle m = -\frac{3}{8}\).

Ejemplo: cálculo de la pendiente a partir de dos puntos

Supongamos que tiene una línea que pasa por 2 puntos: \( (1, 2)\) y \( (4, 11/3)\). Encuentra la pendiente de la recta.

Solución:

Cálculo de la pendiente de una línea

La información proporcionada sobre la línea es que la línea pasa por los puntos \(\displaystyle \left( 1, 2\right)\) y \(\displaystyle \left( 4, \frac{11}{3}\right)\)

Por tanto, el primer paso consiste en calcular la pendiente. La fórmula de la pendiente es: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]

Ahora, reemplazando los números correspondientes es , obtenemos que la pendiente es: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{11}{3} - 2}{ \displaystyle 4 - 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]

Entonces, encontramos que la pendiente es \(\displaystyle m = \frac{5}{9}\) y que la recta pasa por el punto \(\displaystyle \left( 1, 2\right)\)

Conclusión : Con base en los datos proporcionados, concluimos que la pendiente de la recta es \(\displaystyle m = \frac{5}{9}\).

La pendiente de una línea es una de sus propiedades más importantes, junto con la Y-Intercept y intercepción x porque esencialmente definen la línea.