Aprende más sobre esta calculadora de líneas perpendiculares.

Las líneas están determinadas en gran parte por su pendiente (inclinación). Las líneas horizontales son líneas con pendiente igual a cero, y las líneas verticales son líneas en las que la pendiente no está definida (infinito negativo o positivo).

Las líneas perpendiculares son líneas que se cruzan formando un ángulo recto. Existe una condición específica para la pendiente y la pendiente perpendicular siempre que las pendientes estén definidas, para que las rectas sean perpendiculares, es necesario que el producto de las pendientes sea -1.

Observa que una línea dada tiene infinitas líneas perpendiculares a ella. Para encontrar la que buscas, tienes que fijar un punto por el que pasa.

¿Cómo se encuentra la perpendicular de una recta?

La estrategia es sencilla. El paso es encontrar la pendiente de la línea dada. Si se le proporciona la pendiente y el intercepto para definir la línea, entonces ya tiene la pendiente.

De lo contrario, tal vez tenga dos puntos por los que pasa la línea , en cuyo caso se puede calcular la pendiente directamente.

En última instancia, si defines tu línea dada con una ecuación, tienes que meter esa ecuación en el forma de intersección de pendientes , así que para conseguir la pendiente.

Una vez que se tiene la pendiente de la recta dada, se utiliza la fórmula de la pendiente perpendicular, multiplicando por menos uno el recíproco de la pendiente original.

Cuál es la línea perpendicular de una línea horizontal

La línea perpendicular a una línea horizontal es una línea vertical.

Cuál es la línea perpendicular de una línea vertical

La línea perpendicular a una línea vertical es una línea horizontal.

¿Puedes calcular la línea perpendicular sin puntos

Una vez que se tiene una línea, no hay una sino muchas (infinitas) líneas perpendiculares a la línea dada. Para identificar una recta perpendicular concreta, hay que proporcionar un punto por el que pase la recta.

Por lo general, usted proporcionará un punto en la línea original, por donde quiere que pase la línea perpendicular.

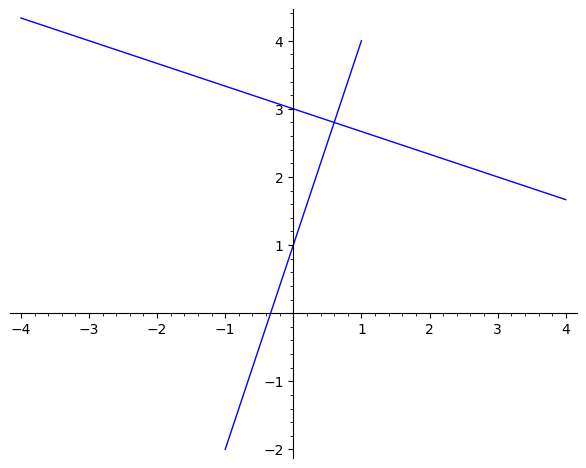
Ejemplo de cálculo de una recta perpendicular para una recta dada:

Considera la recta de ecuación \(2x + 3y = 5)\). Encuentra la ecuación de la recta perpendicular que pasa por \((1, 1)\).

Solución: Primero obtenemos la ecuación de intercepción de la pendiente para la línea DADA, si es posible

Nos han proporcionado la siguiente ecuación:

\[\displaystyle 2x+3y=5\]

Poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle 3y = -2x +5\]

Entonces, resolviendo para \(y\), dividiendo ambos lados de la ecuación por \(3\), se obtiene lo siguiente

\[\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\]

Fórmula De La Pendiente Perpendicular

En general, la fórmula necesaria para calcular la pendiente perpendicular, \(m_{\perp}\), es:

\[m_{\perp} = \displaystyle -\frac{1}{m}\]

Introduciendo el valor de \(m = \) en la fórmula, encontramos que la pendiente perpendicular es

\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{} = \frac{3}{2}\]

Construcción De Líneas Perpendiculares

Ahora, hemos calculado que la pendiente de la perpendicular es \(m_{\perp} = \frac{3}{2}\) y sabemos que la recta perpendicular pasa por el punto \((1, 1)\).

Por lo tanto, con la información que tenemos, podemos construir directamente la forma punto-pendiente de la línea, que es

\[\displaystyle y - y_1 = m_{\perp} \left(x - x_1\right)\]

y, a continuación, insertando los valores conocidos de \(\displaystyle m_{\perp} = \frac{3}{2}\) y \(\displaystyle \left( x_1, y_1 \right) = \left( 1, 1\right)\), obtenemos que

\[\displaystyle y-1 = \frac{3}{2} \left(x-1\right)\]

Ahora, tenemos que expandir el lado derecho de la ecuación distribuyendo la pendiente, por lo que obtenemos \[\displaystyle y = \frac{3}{2} x + \frac{3}{2} \left(-1\right) + 1\]

y simplificando obtenemos que \[\displaystyle y=\frac{3}{2}x-\frac{1}{2}\]

Por tanto, concluimos que la ecuación de la recta dada es \(\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\) y la ecuación de la recta perpendicular es \(\displaystyle y=\frac{3}{2}x-\frac{1}{2}\).

Si quieres que las cosas sean más directas, utiliza esto Calculadora de pendientes perpendiculares y utilizar la fórmula de la recta perpendicular para obtener directamente la pendiente de la recta que es perpendicular.

Esto es para el caso de que sólo seas buscando la pendiente en el contexto de lo que está haciendo.