Calculadora de forma de línea punto-pendiente
Instrucciones: Usa esta calculadora para encontrar la forma pendiente-intersección de la línea que proporcionas, con todos los pasos que se muestran. Con ese fin, debe proporcionar información sobre la línea que desea poner en forma de punto-pendiente.
Hay varias maneras diferentes de informarnos acerca de su línea. Puede proporcionar: (1) tanto la pendiente como la intersección con el eje y, (2) puede escribir cualquier ecuación lineal (p. ej., \(x + 3y = 2 + \frac{2}{3}x\)), (3) puede indicar la pendiente y un punto en el que la recta pasa, o (4) puede indicar dos puntos por donde pasa la línea.
Acerca de esta calculadora de forma punto-pendiente de la recta.
Esta calculadora de ecuación punto-pendiente le proporcionará un cálculo paso a paso de la ecuación de la línea en forma de punto-pendiente para cualquier línea que haya proporcionado inicialmente.
Lo que debe hacer es identificar la línea con la que desea trabajar. Esta línea se puede identificar de muchas maneras diferentes y usted seleccionará según la información que haya proporcionado.
Una de las formas más comunes es definir una línea proporcionando su pendiente y su Y-Intercept , pero ciertamente no es la única manera.
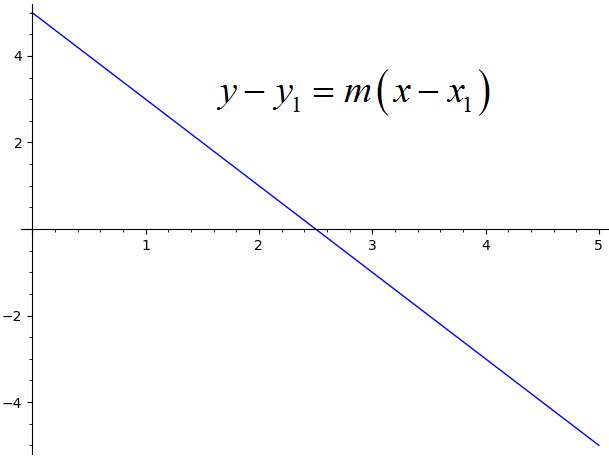
¿Cómo representar una línea en forma de punto-pendiente?
Se dice que una recta está en forma punto-pendiente si se puede escribir como:
\[y - y_1= m (x -x_1)\]En este contexto, \(m\) se identifica como la pendiente de la línea, y \((x_1, y_1)\) es un punto por el que pasa la línea.
¿Cómo puedes encontrar el punto de intersección con una calculadora?
Si conoce la pendiente \(m\) de la línea y un punto \((x_1, y_1)\) por donde pasó la línea, entonces el proceso es fácil y directo, pero podría ser más complicado si tiene la línea definida usando otro tipo de información.
¿Por qué es útil la forma punto-pendiente de una recta?
La forma punto-pendiente es útil porque da una interpretación directa de la pendiente de la línea como la tasa de cambio. De hecho, directamente de la forma punto-pendiente obtenemos
\[\frac{y-y_1}{x-x_1} = m\]¿Puedo obtener la forma de pendiente de punto con dos puntos?
¡Sí! Si tiene dos puntos, utilícelos primero para calcular la pendiente \(m\), y luego elija cualquiera de los puntos para aplicar directamente la fórmula
\[y - y_1= m (x -x_1)\]
Ejemplo: Cálculo de forma Punto-Pendiente
Suponga que sabe que la línea pasa por los puntos \(( \frac{1}{3}, 2)\) y \((\frac{7}{2}, 3)\). Halla la forma punto-pendiente de la recta.
Respuesta:
La información proporcionada sobre la recta es que ésta pasa por los puntos\(\displaystyle \left( \frac{1}{3}, 2\right)\) y \(\displaystyle \left( \frac{7}{2}, 3\right)\)
Por lo tanto, el primer paso consiste en calcular la pendiente. La fórmula de la pendiente es \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]
Ahora, enchufando los números correspondientes es , obtenemos que la pendiente es: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 3 - 2}{ \displaystyle \frac{7}{2} - \frac{1}{3}} = \frac{ \displaystyle 1}{ \displaystyle \frac{19}{6}} = \frac{6}{19}\]
Entonces, ahora sabemos que la pendiente es \(\displaystyle m = \frac{6}{19}\) y que la recta pasa por el punto \(\displaystyle \left( \frac{1}{3}, 2\right)\)
Por lo tanto, con la información que tenemos, podemos construir directamente la forma punto-pendiente de la línea, que es
\[\displaystyle y - y_1 = m \left(x - x_1\right)\]y, a continuación, insertando los valores conocidos de \(\displaystyle m = \frac{6}{19}\) y \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, 2\right)\), obtenemos que
\[\displaystyle y-2 = \frac{6}{19} \left(x-\frac{1}{3}\right)\]Conclusión : Con base en los datos proporcionados, concluimos que la ecuación de la línea en forma de punto-pendiente es \(\displaystyle y-2=\frac{6}{19}\left(x-\frac{1}{3}\right) \).
También puede utilizar nuestro Calculadora de forma estándar y calculadora pendiente-intersección de una línea, si esos son los formatos que le interesan.




