Más sobre esta ecuación de línea en calculadora de forma estándar

Esta ecuación de la línea en la calculadora de ecuaciones de forma estándar le permitirá definir una ecuación en una de las cuatro formas que prefiera, y le mostrará todos los pasos necesarios.

¿Cómo encontrar la ecuación de una recta? Así que lo primero, es definir una ecuación lineal. Para este propósito, puede proporcionar una ecuación directamente o, de lo contrario, según la información que tenga disponible, puede proporcionar:

(1) la pendiente y el intercepto en y.

O (2) la pendiente y un punto por donde pasa la línea,

o (3) puede proporcionar dos puntos por donde pasa la línea.

La forma que utilizará para definir su ecuación dependerá de la información que tenga disponible.

¿Cuál es el formato de una ecuación lineal en forma estándar?

Se dice que una ecuación lineal está en forma estándar si tiene la siguiente estructura:

\[a x + by = c\]

Luego, su objetivo es determinar la fórmula de forma estándar y encontrar las constantes a, b y c que la determinan.

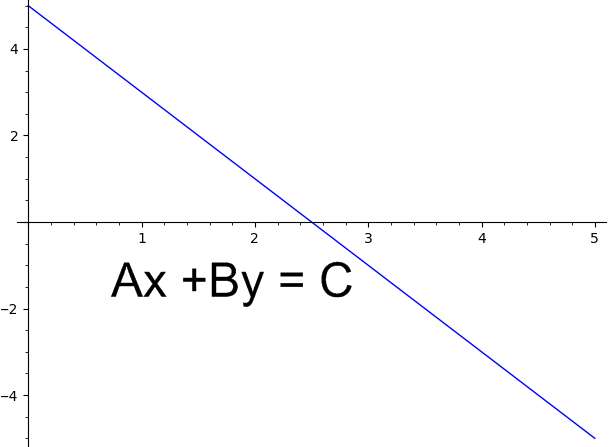
¿Cómo se resuelve la forma estándar en una calculadora?

Con esta calculadora, todo lo que tienes que hacer es proporcionar información para definir la ecuación, entre las cuatro opciones diferentes.

¿Por qué es necesario el formulario estándar?

Ciertas formas específicas de una ecuación provienen de la tradición, pero generalmente porque es útil usar una forma específica.

En el caso de la forma estándar, es práctico tenerla en la forma \(a x + by = c\), porque reemplazando \(x=0\) es fácil calcular la Y-Intercept , y reemplazando \(y=0\) es fácil calcular el intercepción x .

Además, la forma estándar se usa comúnmente como el formato de elección al resolver sistemas simultáneos de ecuaciones lineales .

¿Puede este salculadora tratar con ecuaciones lineales fraccionarias?

Una de las ventajas de esta calculadora es que todos los coeficientes que utiliza para definir la ecuación pueden ser cualquiera expresión numérica genérica , que incluye fracciones .

Para ver un ejemplo de cómo esta calculadora trata con ecuaciones lineales fraccionarias, consulte el siguiente ejemplo.

Ejemplo: Cálculo de la ecuación de una recta

Suponga que tiene una línea que pasa por el punto \(\left( \frac{1}{3}, \frac{2}{3}\right)\) con pendiente \(m = \frac{1}{2}\). Encuentre la forma estándar de la línea.

Respuesta:

La información proporcionada inicialmente sobre la recta es que la pendiente es \(\displaystyle m = \frac{1}{2}\) y la recta pasa por el punto \(\displaystyle \left( \frac{1}{3}, \frac{2}{3}\right)\)

Por lo tanto, con la información que tenemos, podemos construir directamente el forma punto-pendiente de la recta , cual es

\[\displaystyle y - y_1 = m \left(x - x_1\right)\]

y, a continuación, insertando los valores conocidos de \(\displaystyle m = \frac{1}{2}\) y \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, \frac{2}{3}\right)\), obtenemos que

\[\displaystyle y-\frac{2}{3} = \frac{1}{2} \left(x-\frac{1}{3}\right)\]

Ahora, tenemos que expandir el lado derecho de la ecuación distribuyendo la pendiente, por lo que obtenemos \[\displaystyle y = \frac{1}{2} x + \frac{1}{2} \left(-\frac{1}{3}\right) + \frac{2}{3}\]

y simplificando obtenemos que \[\displaystyle y=\frac{1}{2}x+\frac{1}{2}\]

Pasar la variable independiente al lado izquierdo de la ecuación conduce a la siguiente forma estándar de la línea:

\[\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\]

Conclusión : Con base en los datos provistos, concluimos que la ecuación de la recta en forma estándar es \(\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\).

Otras calculadoras útiles relacionadas con funciones lineales

Muchas veces, solo desea echar un vistazo rápido a cómo se ven las cosas gráficamente, para lo cual podría usar esta herramienta para graficar ecuaciones lineales

O también puedes graficar dos ecuaciones lineales y encontrar la intersección de dos rectas , si existiera.

Como paso previo, es posible que desee calcular primero la pendiente, por lo que para usted la forma pendiente-intersección, para la cual podría usar esto pendiente de una calculadora de fórmula de línea .