Más sobre derivadas trigonométricas

Use esta calculadora para encontrar derivadas trigonométricas, que en este caso suponemos que es cualquier función diferenciable válida que involucre una o más funciones trigonométricas elementales.

Un ejemplo de una función válida para esta calculadora es f(x) = sin(x)/x, o f(x) = x*sin(x^3), solo para dar un ejemplo.

Luego, cuando ya haya escrito la función correspondiente, puede hacer clic en el botón "Calcular", para obtener todos los pasos del cálculo de la derivada que se le muestran.

Las funciones trigonométricas juegan un papel crucial en el cálculo, así como en calcular derivadas en general. En última instancia, las funciones más complejas pueden reducir sus derivadas al cálculo de la derivada para funciones trigonométricas más simples.

Derivadas trigonométricas básicas

La idea de usar reglas de derivadas es descomponer una función compleja y diferenciarla usando las derivadas de funciones conocidas. Específicamente, funciones trigonométricas simples como seno, coseno, tangente y cotangente jugarán un papel importante en eso.

¿cuáles son las derivadas trigonométricas básicas?

• Derivada Trigonométrica 1: $\frac{d}{dx} \sin (x) = \cos(x)$
• Derivada Trigonométrica 2: $\frac{d}{dx} \cos (x) = -\sin(x)$
• Derivada Trigonométrica 3: $\frac{d}{dx} \tan (x) = \sec^2(x)$
• Derivada Trigonométrica 4: $\frac{d}{dx} \cot (x) = -\csc^2(x)$
• Derivada Trigonométrica 5: $\frac{d}{dx} \sec (x) = \sec(x)\tan(x)$
• Derivada Trigonométrica 6: $\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)$

Estas son las derivadas básicas que necesita saber muy bien y posiblemente memorizar para usar Reglas Derivadas para calcular derivadas más complicadas

¿las derivadas trigonométricas están en grados?

No, la derivada de las funciones trigonométricas está en radianes , por lo que las derivadas trigonométricas encontradas reflejan el hecho de que el argumento x se mide en radianes.

Entonces, por ejemplo, supongamos que queremos calcular la derivada de sen en grados , por lo que definimos $f(y) = \sin(y)$, donde $y$ se mide en grados.

Ahora, sea $x = \frac{\pi y}{180}$ el ángulo equivalente en radianes y también resolviendo para $y$ encontramos que $y = \frac{180 x}{\pi}$, entonces usando la regla de la cadena:

$$\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y)$$

Entonces, en base a esto, la derivada del seno en grados es en realidad coseno en grados, pero multiplicado por un factor $\frac{180}{\pi}$.

¿cómo se encuentran las derivadas en trigonometría?

Los derivados trigonométricos se encuentran por definición, utilizando identidades trigonométricas básicas. Por ejemplo, usando el seno de la fórmula de la suma podemos derivar la derivada de $\sin(x)$, usando la definición de límite:

$$\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)$$

Consejos y trucos

Lo principal para usted es recordar siempre lo que el 6 derivadas trigonométricas son , y conócelos de memoria, ya que los usarás continuamente, junto con los básicos reglas diferenciadoras .

De manera similar, puede usar identidades trigonométricas y la definición de función inversa para encontrar las derivadas trigonométricas inversas más comunes.

Ejemplo: cálculo de la derivada trigonométrica

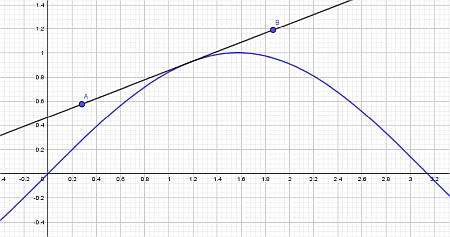
Considere la siguiente función: $f(x) = \sin^2(x)+ \frac{1}{x}$. encuentra su derivada

Solución: Las derivadas trigonométricas implican funciones trigonométricas que deben diferenciarse. Considere la función $\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}$, que contiene una función seno, por lo que califica como una derivada trigonométrica.

Resultados : Para este ejemplo, se encuentra que la derivada es:

$$f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}$$

Es muy útil representar la función y su derivada en un gráfico. Vea abajo:

Ejemplo la derivada de una función trigonométrica

Considere la siguiente función trigonométrica: $f(x) = \sin(x) + x \cos(x)$, encuentre su derivada.

Solución: Ahora, necesitamos trabajar con la derivada de la siguiente función trigonométrica $\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)$.

Conclusión Final : Concluimos que la derivada está dada por:

$$f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)$$

Se obtiene el siguiente gráfico:

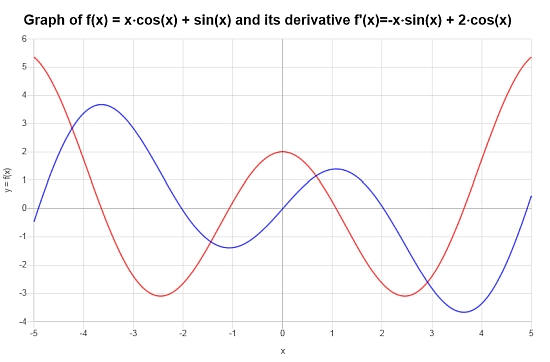
Ejemplo: derivadas trigonométricas y diferenciación implícita

Encuentra $\frac{dy}{dx}$ para $\sin(x)+\cos(y) = 1$.

Solución: necesitamos usar diferenciación implícita , por lo que diferenciamos ambos lados y usamos el Cadena De Reglas :

$$\frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right)$$ $$\Rightarrow \cos(x)-\sin(y)y' = 0$$ $$\Rightarrow \sin(y)y' = \cos(x)$$ $$\Rightarrow y' = \frac{\cos(x)}{\sin(y)}$$

con lo que se concluye el cálculo.

Otras calculadoras de derivadas útiles

encontrar la derivada de funciones simples y elementales es la piedra angular del proceso de encontrar las derivadas de funciones más complicadas, mediante el uso de la conocida reglas de diferenciación .

En este contexto, básico funciones trigonométricas pueden considerarse funciones elementales cuya derivada puede calcularse mediante límites, a través de su propia definición. Entre las funciones elementales más útiles tenemos polinomios y funciones racionales.