Acerca de esta calculadora de pecado

Este calculadora de pecado le ofreceremos lo siguiente: puede proporcionar una expresión numérica como sin(pi/4), en cuyo caso la calculadora la simplificará y le dará un valor numérico aproximado si es necesario. Además, si proporciona una función sin como sin(3x+1), la calculadora la graficará.

Entonces, el proceso es simple: una vez que haya proporcionado la expresión de pecado desea calcular, simplemente haga clic en el botón "Calcular" que se encuentra debajo del formulario para obtener los pasos de la solución.

seno, junto con coseno son dos piedras angulares de la trigonometría. Verás seno y coseno por todas partes cuando resolver triángulos , por ejemplo, sino también en campos como la Física.

¿cómo se calcula el pecado?

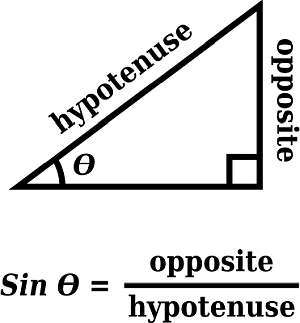
El pecado es uno de los bloques de construcción básicos en Geometría y Trigonometría. Sin es una cantidad que se puede calcular para ángulos en el contexto de un triángulo rectángulo. Cuando tienes uno de los ángulos en un triángulo rectángulo que no es el 90 _O uno, puedes encontrar el lado opuesto y el lado adyacente .

Entonces, la fórmula para el pecado es

\[\sin \theta = \frac{\text{Opposite Side} }{ \text{Hypothenuse} }\]

¿a qué es igual el pecado?

Sin es una cantidad adimensional, que mide el tamaño de la inclinación de un ángulo con respecto a la referencia horizontal, donde se asienta el lado adyacente.

Cuando sen es cero, entonces el ángulo es cero, por lo que no hay apertura. La apertura máxima del ángulo ocurre cuando sen = 1, que ocurre en 90 _O .

¿qué es el pecado de 1?

Esa pregunta puede parecer inocente, pero muchas veces genera confusión. En matemáticas formales, todas las funciones trigonométricas se medirán en radianes de forma predeterminada. Pero por alguna razón, los radianes no son muy conocidos o son demasiado populares entre los estudiantes, quienes prefieren usar los grados como medida, simplemente porque les resulta más familiar.

Los alumnos conocen bien los ángulos notables en grados como 90 _O siendo el ángulo recto, y 360 _O siendo el círculo completo. Puedes usar esto calculadora de grados a radianes moverse entre los dos sistemas.

Entonces, la respuesta correcta a qué es sin(1) es que sin(1) es aproximadamente 0.841471, cuando se supone que el ángulo 1 está en radianes. Ahora, sin(1) es aproximadamente 0.017452 cuando se supone que 1 se expresa en grados. Entonces, se debe tener extremo cuidado cuando se trata de ángulos.

¿cuánto es el seno del 1 negativo?

Otra pregunta que formalmente tiene una respuesta simple, pero a veces depende de la convención utilizada. El seno al 1 negativo debe especificarse más, ya que el seno es una función. Así que puedes hacer sin(1), y eso es un número, y sin(1) al menos 1 es simplemente tomar el inverso del número sin(1), entonces tienes 1/sin(1), que es un número.

Sin embargo, muchas veces, seno a 1 negativo significa referirse a la 'función inversa del seno', que se conoce como la función arcsen, o a veces a algunas personas les gusta usar la nomenclatura de \(sin^{-1}(x)\).

¿puedo usar una calculadora científica para calcular el pecado?

De hecho, puede, pero una de las ventajas de usar este calculadora de pecado es que obtendrá los pasos que se muestran junto con el resultado. La mayoría de las calculadoras solo mostrarán la respuesta final.

¿cómo usar una calculadora de pecado?

La idea principal de una calculadora de pecado es evaluar las expresiones de pecado que proporcione. Hay algunos ángulos notables, generalmente múltiplos o fracciones de \(\pi\) que son resultados simples, enteros o fraccionarios al calcular su seno, por lo que es una buena idea usar una calculadora de expresión de seno para ayudarlo con eso.

No es fácil recordar todos los cálculos de pecado para TODOS los ángulos notables, y terminarás trabajando con un triángulo, tratando de obtener la respuesta manualmente, y una calculadora será útil para verificar dos veces lo que obtienes manualmente.

Además, en su lugar, puede alimentar la calculadora con una función sin, como sin (pi x), y en lugar de evaluar algunos puntos, esta calculadora le dará el gráfico correspondiente

¿cuáles son los pasos para usar una calculadora de pecado?

• Paso 1: Identifique la expresión del pecado que desea calcular
• Paso 2: Escriba la expresión en el cuadro correspondiente. No necesitas simplificar previamente, la calculadora lo hará por ti
• Paso 3: La calculadora verificará si es una expresión que se puede evaluar, en cuyo caso la reducirá a sus términos más simples
• Paso 4: si sin todavía está en la expresión porque no se pudo simplificar más, como sin (3/4), la calculadora le dará un valor numérico aproximado
• Paso 5: si en su lugar se proporciona una función sin, se proporcionará un gráfico

No podemos enfatizar lo suficiente la importancia de calcular correctamente las operaciones que involucran el seno, ya que aparecerán literalmente en todas partes.

Fórmula de seno y coseno

El seno y el coseno son dos primos muy cercanos, si no hermanas. Existe una estrecha relación entre ellos, expresada en la siguiente fórmula:

\[\displaystyle \sin\left(\frac{\pi}{2} - x \right) = \cos(x) \]

Además, otra fórmula que vincula de forma íntima el seno y el coseno es:

\[\displaystyle \sin^2(x) + \cos^2(x) = 1 \]

¿por qué es tan importante el pecado?

Los senos son importantes porque, junto con los cosenos, están en el centro y el núcleo de la construcción de un círculo. Y luego los círculos albergan muchas otras construcciones, como triángulos, etc.

El seno y el coseno terminan enredados en cada construcción geométrica, en consecuencia.

Ejemplo: calculadora de pecado

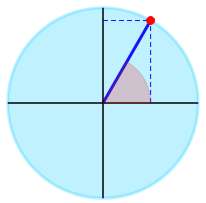
Calcula la siguiente expresión de pecado: \(\sin\left(\frac{\pi}{3}\right)\)

Solución: Se ha proporcionado la siguiente expresión trigonométrica para ser calculada:

\[ \sin\left(\frac{\pi}{3}\right)\]

Al inspeccionar la expresión trigonométrica dada, podemos encontrar un ángulo notable, que es \(\sin\left(\frac{\pi{}}{3}\right)\).

▹ Para el ángulo \(\frac{\pi{}}{3}\) obtenemos gráficamente:

La expresión trigonométrica dada se puede simplificar como:

Conclusión: Concluimos que \(\displaystyle \sin\left(\frac{\pi}{3}\right) = \frac{1}{2}\sqrt{3} \approx 0.866\).

Ejemplo: más cálculos de seno

Calcula lo siguiente: \( \sin\left(\frac{5}{4}\right) \)

Solución: Se ha proporcionado la siguiente expresión trigonométrica para ser calculada:

\[ \sin\left(\frac{5}{4}\right)\]

pero esta expresión trigonométrica dada no puede simplificarse más.

Conclusión: La función pasada no se puede simplificar y obtenemos aproximadamente \(\displaystyle \sin\left(\frac{5}{4}\right) \approx 0.949\).

Ejemplo: función sin

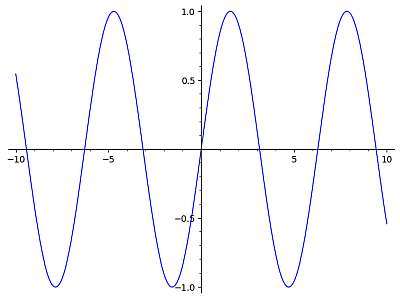
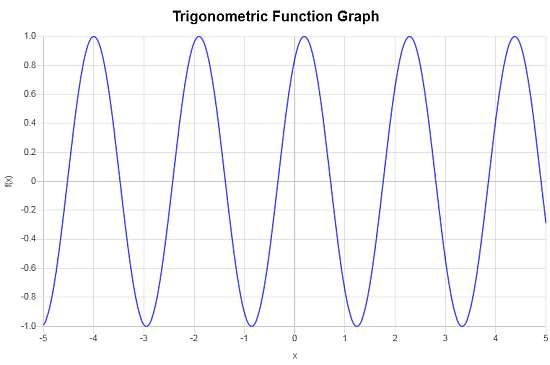
Calcula \( \sin(3x + 1) \).

Solución: Necesitamos trabajar con la siguiente función trigonométrica

\[f(x) = \sin\left(3x+1\right)\]

Con base en el argumento de la función trigonométrica que se pasó, la frecuencia y el período se calculan de la siguiente manera:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

y también

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

Con base en la función trigonométrica proporcionada, \(f(x) = \sin\left(3x+1\right)\), obtenemos que:

» La amplitud en este caso es \(A = 1\).

» El cambio de fase es igual a \(\displaystyle\frac{-1}{3} = -0.3333\).

» El desplazamiento vertical es igual a \( 0\).

Resumiendo, se ha encontrado lo siguiente para la función trigonométrica dada

• Período = \(2.0944\)
• Frecuencia = \(0.4775\)
• Amplitud = \(1\)
• Cambio de fase = \(-0.3333\)
• Desplazamiento vertical = \(\displaystyle 0\)

El siguiente es el gráfico correspondiente.

Más calculadoras trigonométricas

La trigonometría combina todos estos conceptos, incluidos círculos y triángulos, y tanto el pecado como por qué están en el centro mismo de la misma.

Tratando con expresiones trigonométricas es otra habilidad crucial que es muy importante que usted adquiera.