Acerca de la regla de la cadena

Esta calculadora le permitirá aplicar la regla de la cadena a cualquier función compuesta que proporcione. A Función compuesta corresponde al caso cuando evalúas una función dentro de una función. Para que la calculadora de la regla de la cadena funcione, debe proporcionar una función compuesta diferenciable y válida.

Un ejemplo de una función válida sería f(x) = (sin(x))^2, donde aquí tenemos la función 'x^2' que está siendo evaluada en otra función, que es sin(x), formando un función compuesta.

Una vez que se ha proporcionado una función diferenciable válida, lo siguiente que debe hacer es hacer clic en el botón que dice "Calcular", que luego pondrá en marcha los cálculos y se le mostrarán todos los pasos.

La derivada de la regla de la cadena es una de las reglas de diferenciación más utilizadas. Esto se debe a que la composición de funciones es una de las formas más naturales de construir nuevas funciones basadas en funciones elementales.

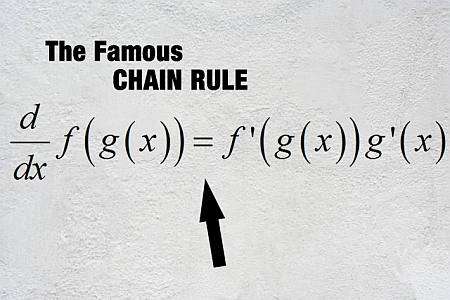
¿qué es la regla de la cadena?

En palabras simples, la regla de la cadena permite diferenciar funciones compuestas, esto es, funciones que se evalúan dentro de otras funciones. Entonces, digamos que tenemos la función \(f(x)\) y \(g(x)\), y sabemos cómo calcular la derivada de estas funciones, que son \(f'(x)\) y \(g'(x)\).

Entonces, hay un Fórmula de la regla de la cadena que nos permite calcular la derivada de la función compuesta \(f \circ g\), que se define como \((f \circ g)(x) = f(g(x))\):

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

Pasos para usar la regla de la cadena

• Paso 1: Identificar la función externa f(x) y la función interna g(x)
• Paso 2: Asegúrese de que f(x) y g(x) sean funciones diferenciables válidas y calcule las derivadas correspondientes f'(x) y g'(x)
• Paso 3: Usa la fórmula (f \circ g)'(x) = f'(g(x))g'(x), que indica que evaluamos la derivada de la función externa en la función interna, y la multiplicamos por la derivada de la función interna

Observe cómo los pasos anteriores utilizan la idea de función 'interna' y 'externa'. Posiblemente no sea un término estándar, sino más bien una idea que puede ayudarte a identificar el papel que juega cada función cuando usas la regla de la cadena.

Aplicaciones de la regla de la cadena

La regla de la cadena es de hecho una excelente herramienta para encontrar derivadas, y normalmente será la clave de cualquier calculadora de derivadas , junto con todos los demás básicos Reglas Derivadas . Pero la regla de la cadena tiene una interpretación especial en lo que se llama Tarifas Relacionadas

Para dar contexto a la idea de las tasas relacionadas, comencemos con una forma de escribir la regla de la cadena que tal vez a mucha gente le resulte más fácil de entender:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

La forma anterior de la regla de la cadena dice que si \(y\) es una función de \(z\) y \(z\) es una función de \(x\), entonces, en última instancia, \(y\) es una función de \(x\), y puedes encontrar la derivada de \(y\) con respecto a \(x\) usando la regla de la cadena.

Como probablemente haya sospechado, \(y\) desempeña el papel de \(f(x)\) (la función 'externa') y \(z\) desempeña el papel de \(g(x)\) (la función 'interna').

La forma anterior de la regla de la cadena vincula la tasa de cambio de y con respecto a x, con las tasas de cambio de y con respecto a z y la de z con respecto a x, y de ahí el término "tasas relacionadas".

Esto es extremadamente útil en la práctica. Ejemplo: el radio de un círculo aumenta a razón de 2 cm/s, ¿cuál es la tasa de cambio del área del círculo? Entonces, puedes ir y expresar el radio del círculo como una función de t, reflejando el hecho de que aumenta a una tasa de 2 cm/seg, O puedes usar la regla de la cadena.

Entonces llamas a A el área, r al radio y t al tiempo. Lo que necesitas calcular es \(\displaystyle \frac{dA}{dt}\), entonces usas la regla de la cadena directamente, ya que conoces \(A = \pi r^2\), y r'(t) = 2, entonces

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

Regla de la cadena de derivadas parciales

¿Puedes usar la regla de la cadena con Derivadas parciales ? Por supuesto, la diferenciación parcial es como la diferenciación regular, solo que se supone que las otras variables son constantes, por lo que entonces lo habitual Reglas Derivadas aplicar.

Entonces, se aplica el ideal de la regla de la cadena multivariable, solo que una variable varía a la vez.

Integración de la regla de la cadena

La regla de la cadena en el sentido de que no se aplica como una herramienta de derivación, sino que se convierte en una herramienta de integración invaluable para sustituciones y cambios de variables.

Puede concebirse como una especie de regla de cadena inversa.

Ejemplo: uso de la regla de la cadena

Calcular la derivada de la función: \(f(x) = \sin(\cos(x)) \)

Solución: Considere la función \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\). Esta función corresponde a la composición de dos funciones: sen(x) y cos(x), por lo que en este caso se aplicaría la Regla de la Cadena.

cual es la conclusion : Podemos concluir que la derivada que buscamos es:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

y esto concluye el cálculo.

Ejemplo de regla de cadena

Usando la regla de la cadena y cualquier otra regla derivada, calcule: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

Solución: En este ejemplo tenemos la función \(\displaystyle f(x)=\cos\left(x^2\right)\), que corresponde a una función compuesta, lo que indica que la regla de la cadena es la regla de la derivada correcta para empezar (se necesitarán otras reglas a lo largo de los cálculos)

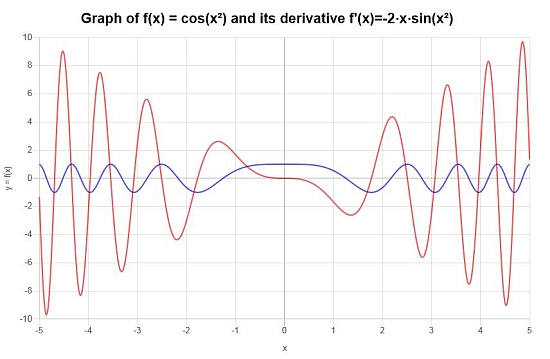
Derivada Final : La conclusión es que la derivada de la función dada está dada por:

\[f'(x) = -2x\sin\left(x^2\right)\]

Podemos construir la siguiente representación gráfica en el intervalo \([-5, 5]\):

Ejemplo: otro cálculo de la regla de la cadena

Calcule la derivada de \( f(x) = x^2 \sin(x^2)\) utilizando la regla de la cadena.

Solución:

Se ha proporcionado la siguiente función: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), para la cual necesitamos calcular su derivada.

La función ya vino simplificada, por lo que podemos proceder directamente a calcular su derivada:

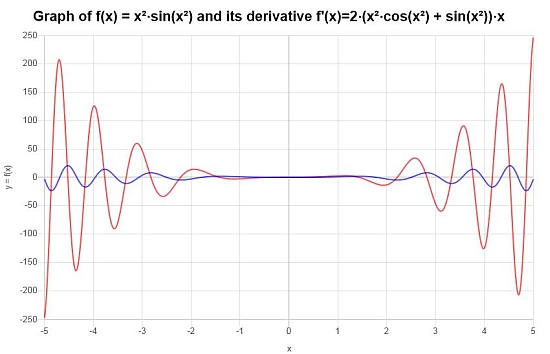
cual es la conclusion final : La conclusión final es que la derivada que buscamos está dada por:

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

Gráficamente tenemos:

Otras calculadoras de derivadas

ciertamente usando un calculadora de derivadas facilitará las cosas cuando se trata de funciones bastante complicadas. El proceso de diferenciación se vuelve más amplio facilitado por el uso de términos comunes y fáciles de recordar. Reglas Derivadas , incluyendo el Regla Del Producto el Regla Del Cociente y el Cadena De Reglas .

Estas reglas te ayudarán a manejar todas las funciones diferenciables, pero el proceso algebraico del cálculo y simplificación puede no ser necesariamente fácil.