Más sobre esta calculadora de vértices

Esta calculadora le permitirá obtener una función cuadrática que proporcione en Forma de vértice , mostrando todos los pasos. Debe proporcionar una expresión cuadrática válida en x. Cualquier función cuadrática válida funcionará.

Por ejemplo, puede proporcionar algo como x ^ 2 + 3x + 4, o tal vez podría proporcionar una expresión que no esté simplificada, como x ^ 2 + 3x - 1/2 x + 3x ^ 2 - 3.

Una vez que proporcione una función cuadrática válida, simplemente haga clic en "Calcular" y se le mostrará el cálculo de la forma de vértice, con todos los pasos proporcionados por este Calculadora de parábola .

Toda función cuadrática que esté válidamente definida tendrá una forma de vértice, de la cual será directo obtener las coordenadas del vértice, y si la parábola abre "hacia arriba" o "hacia abajo".

¿cómo encontrar la forma del vértice de una parábola?

Todas las funciones cuadráticas se representan gráficamente mediante una parábola. Esta parábola se abrirá hacia arriba o hacia abajo, según el signo del coeficiente principal.

En última instancia, poner la parábola en forma de vértice consiste en encontrar el vértice de la función cuadrática, lo cual se logra mediante Completando el cuadrado .

¿cuáles son los pasos para calcular la forma del vértice?

Asi Que, ¿Cómo encuentras la forma del vértice? ? Puedes seguir estos pasos:

• Paso 1: Identifica la función cuadrática. La expresión debe tener grado 2, y el coeficiente principal que multiplica x² debe ser diferente de cero
• Paso 2: Si el coeficiente principal que multiplica x² es positivo, la parábola abre hacia arriba, y si es negativo, abre hacia abajo
• Paso 3: Complete los cuadrados y observe el término dentro de los paréntesis con x, porque determina la coordenada x del vértice.
• Paso 4: Después de completar los cuadrados, la constante fuera del paréntesis (podría ser cero) corresponde a la coordenada y del vértice

Por tanto, podemos ver que el proceso general de cálculo de la forma de los vértices está estrechamente relacionado con el proceso de completar los cuadrados.

¿hay una fórmula de vértice?

De hecho, sí, lo hay. Normalmente, el proceso de completar los cuadrados es el camino más largo. Suponga que tiene un función cuadrática , expresado por:

\[ f(x) = a x^2 + b x + c\]

Entonces, ya tienes una función cuadrática simplificada. La coordenada x del vértice se calcula con la siguiente fórmula:

\[ x_v = \displaystyle \frac{-b}{2a} \]

Realmente simple, ¿verdad? Sí. Pero entonces, ¿cómo obtienes la coordenada y del vértice? Tomas el valor \(x_v\) y lo reemplazas en la función cuadrática. Entonces obtenemos

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

Naturalmente, esta fórmula puede ser mucho más rápida que hacer un proceso de completar los cuadrados, pero cada método tiene sus usos, y las circunstancias de un problema dado le dirán qué forma usar. .

Forma cuadrática a vértice?

¿Por qué querrías pasar de la forma cuadrática a la de vértice? Hay muchas razones: desde un punto de vista geométrico, la forma del vértice permite ver la función cuadrática dada como una traslación y cambio de escala de una parábola elemental, donde la traslación está determinada por el vértice, y la escala se determina con el principio. coeficiente.

El cálculo puede ser laborioso, pero esto Calculadora de parábola hará el trabajo pesado por ti.

¿forma estándar a vértice?

Por lo general, hay un poco de confusión acerca de esto. Permítanme aclarar, la forma de vértice es otro nombre que se le da a la forma estándar. Entonces entonces, la forma estándar de una función cuadrática \(y = a(x-h)^2 + k\) es la misma que la forma del vértice.

La confusión surge porque a veces las personas usan la forma general de una cuadrática cuando se refieren a la forma estándar. La forma general es \(y = ax^2 + bx + c\).

Entonces, la pregunta que tiene sentido es cómo pasar de la forma general a la forma de vértice, que es lo mismo que preguntar cómo pasar de la forma general a la forma estándar. La respuesta es simple: comienza desde la forma general y luego Completa los cuadrados para llegar a la forma estándar.

Ejemplo: cómo encontrar la forma de vértice

Encuentra el vértice de la siguiente expresión cuadrática \(f(x) = x^2 + 3x - 6\) usando la fórmula del vértice

Solución: Necesitamos encontrar la forma de vértice para la función cuadrática \(\displaystyle f(x)=x^2+3x-6\).

Primero calculamos las coordenadas del vértice de la parábola asociada a la función cuadrática dada.

Para una función cuadrática de la forma \(f(x) = a x^2 + bx + c\), la coordenada x del vértice se calcula usando la siguiente fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

En este caso, tenemos que la función para la que necesitamos encontrar el vértice es \(f(x) = \displaystyle x^2+3x-6\), lo que implica que los coeficientes correspondientes son:

\[a = 1\] \[b = 3\] \[c = -6\]

Sustituyendo los valores conocidos de \(a\) y \(b\) en la fórmula de la coordenada x del vértice, obtenemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -\frac{3}{2}\) en la función cuadrática, por lo que obtenemos:

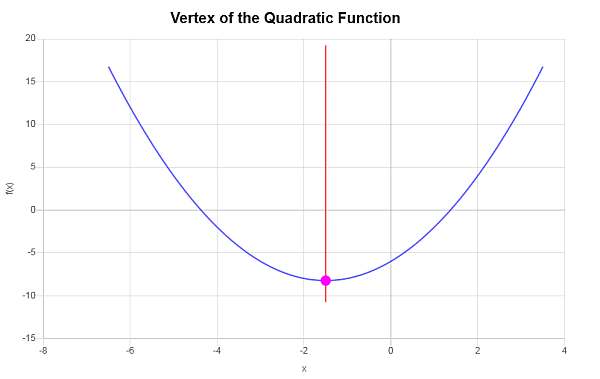
\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -\frac{3}{2}\) y la coordenada y del vértice es \(y_V = \displaystyle -\frac{33}{4}\). Esto indica que el punto que representa el vértice es \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\).

De forma gráfica se obtiene lo siguiente:

Necesitamos completar el cuadrado de la expresión cuadrática \(\displaystyle x^2+6x-2\).

Se deben seguir los siguientes pasos para completar el cuadrado:

Paso 1: En este caso, dado que la constante principal, el término que multiplica \(x^2\) en el polinomio dado, es \(a = 1\), entonces no lo factorizamos.

Paso 2: Forzamos un '2' delante del término \(x\) al observar que el término de orden 1 en la expresión cuadrática dada podemos reescribir: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), entonces obtenemos \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Paso 3: El término que multiplica 2 en este caso es \(\displaystyle 3\), así que para usar la ecuación binomial, necesitamos que su cuadrado \(\displaystyle \left(3\right)^2\) esté en la expresión.

Para lograr eso, ahora sumamos y restamos el término \(\displaystyle \left(3\right)^2 = 9\), para completar el cuadrado. Sumar y restar el mismo término es lo mismo que sumar cero, por lo que no afecta la expresión: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Etapa 4: Completamos el cuadrado y simplificamos las constantes: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusión: Por lo tanto, encontramos que la función en forma de vértice es \(\displaystyle f(x) = \left( x+3 \right)^2-11\), que completa el cálculo.

Ejemplo: forma de cuadrático a vértice

Convierta la siguiente forma cuadrática \(f(x) = x^2 + 6x - 2\) en forma de vértice. ¿Cuáles son las coordenadas del vértice? ¿La parábola abre hacia arriba o hacia abajo?

Solución:

Necesitamos encontrar la forma de vértice para la función cuadrática \(\displaystyle f(x)=x^2+6x-2\).

Primero calculamos las coordenadas del vértice de la parábola asociada a la función cuadrática dada.

Para una función cuadrática de la forma \(f(x) = a x^2 + bx + c\), la coordenada x del vértice se calcula usando la siguiente fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

En este caso, tenemos que la función para la que necesitamos encontrar el vértice es \(f(x) = \displaystyle x^2+6x-2\), lo que implica que los coeficientes correspondientes son:

\[a = 1\] \[b = 6\] \[c = -2\]

Sustituyendo los valores conocidos de \(a\) y \(b\) en la fórmula de la coordenada x del vértice, obtenemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{6}{2 \cdot 1} = -3\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -3\) en la función cuadrática, por lo que obtenemos:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -3\) y la coordenada y del vértice es \(y_V = \displaystyle -11\). Esto indica que el punto que representa el vértice es \( \displaystyle \left(-3, -11\right)\).

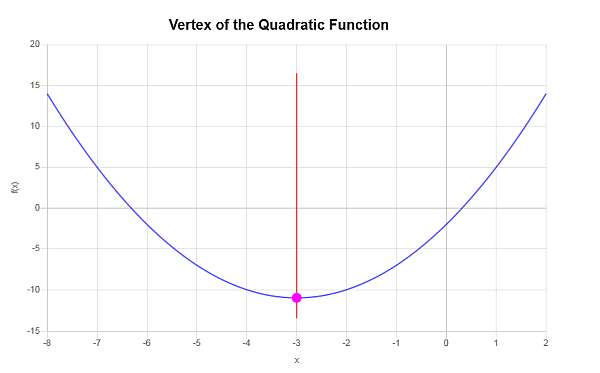
Necesitamos completar el cuadrado de la expresión cuadrática \(\displaystyle x^2+6x-2\).

Se deben seguir los siguientes pasos para completar el cuadrado:

Paso 1: En este caso, dado que la constante principal, el término que multiplica \(x^2\) en el polinomio dado, es \(a = 1\), entonces no lo factorizamos.

Paso 2: Forzamos un '2' delante del término \(x\) al observar que el término de orden 1 en la expresión cuadrática dada podemos reescribir: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), entonces obtenemos \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Paso 3: El término que multiplica 2 en este caso es \(\displaystyle 3\), así que para usar la ecuación binomial, necesitamos que su cuadrado \(\displaystyle \left(3\right)^2\) esté en la expresión.

Para lograr eso, ahora sumamos y restamos el término \(\displaystyle \left(3\right)^2 = 9\), para completar el cuadrado. Sumar y restar el mismo término es lo mismo que sumar cero, por lo que no afecta la expresión: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Etapa 4: Completamos el cuadrado y simplificamos las constantes: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusión: Por lo tanto, encontramos que la función en forma de vértice es \(\displaystyle f(x) = \left( x+3 \right)^2-11\), que completa el cálculo.

Otras calculadoras cuadráticas

La mayoría de calculadoras cuadráticas depender de una forma u otra del proceso de completando los cuadrados , que permite agrupar cosas dentro de paréntesis que están al cuadrado.

Como podemos ver en la fórmula del vértice, el cálculo del vértice está estrechamente relacionado con el Fórmula cuadrática y el cálculo de raíces de la ecuación cuadrática . .