Más sobre la composición de funciones

Esta calculadora te permitirá calcular una función compuesto \(f \circ g\) basado en dos funciones \(f\) y \(g\) que proporcione. Tenga en cuenta que, en general, \(f \circ g\) no es lo mismo que \(g \circ f\), por lo que el orden es relevante.

Al calcular la composición \(f \circ g\), hay una función interna \(g\) y una función externa \(f\), y cambias el orden, muy a menudo el resultado varía.

Observe que \(f\) y \(g\) deben ser funciones válidamente definidas, como por ejemplo \(f(x) = \sqrt{x}\) y \(g(x) = 2x+1\), entonces tendríamos que \((f \circ g)(x) = f(g(x)) = \sqrt{2x+1}\) .

¿qué es una función compuesta?

Para formar una función compuesta, evalúas una función dentro de otra función. Sean funciones \(f\) y \(g\), la función compuesta se define como

\[\displaystyle (f \circ g)(x) = f(g(x)) \]

¿cuáles son los pasos para encontrar la función compuesta?

• Paso 1: Identifique las funciones f y g para las que hará la composición de funciones
• Paso 2: Establecer claramente la función interna y externa. En este caso asumimos que f es la función externa y g es la fórmula interna
• Paso 3: La función compuesta se define como (f◦g)(x) = f(g(x))

Puede simplificar la salida resultante de f(g(x)), y de hecho, la calculadora lo simplificará por usted. Un punto principal de importancia es darse cuenta de que es posible que deba restringir el dominio de la función compuesta para que esté bien definida.

¿qué es una calculadora de niebla?

En este caso, la niebla no es la niebla que conoces, se refiere a la composición de f y g, escrita como \(f \circ g\).

La composición de funciones estará tan involucrada algebraicamente como la complejidad de las funciones que la componen. Es decir, la composición de funciones simples conducirá a una función compuesta simple, que es fácil de calcular.

Usando esta calculadora compuesta

La ventaja de usar esta calculadora compuesta es que obtendrá la función compuesta calculada y simplificada en sus términos más simples, pero también obtendrá la función compuesta graficada.

Cadena de funciones compuesta

La composición se puede aplicar a más de dos funciones. Por ejemplo, considere las funciones \(f\), \(g\) y \(h\). La composición de la cadena se define como

\[\displaystyle (f \circ g \circ h)(x) = f(g(h(x))) \]

donde el orden en que se componen las expresiones es relevante.

Dominio de la calculadora de funciones compuestas

Observe que el dominio de una función compuesta puede ser diferente al de las dos funciones originales. Por ejemplo, veamos nuevamente el caso de \(f(x) = \sqrt{x}\) y \(g(x) = 2x+1\). El dominio de f es \([0, \infty)\) y el dominio de g es \((-\infty, \infty)\), pero como \((f\circ g)(x) = \sqrt{2x+1}\), el dominio de \(f\circ g\) es \([-\frac{1}{2}, \infty)\).

Ejemplo: composición de funciones

Calcular y graficar: \((f \circ g)(x)\) para \(f(x) = \sqrt{x}\) y \(g(x) = 2x-1\).

Solución: Se han proporcionado las siguientes funciones: \(\displaystyle f(x)=\sqrt{x}\) y \(\displaystyle g(x)=2x-1\), para lo cual necesitamos calcular la función compuesta \(f \circ g\).

Por definición, la función compuesta \(f \circ g\) se define como:

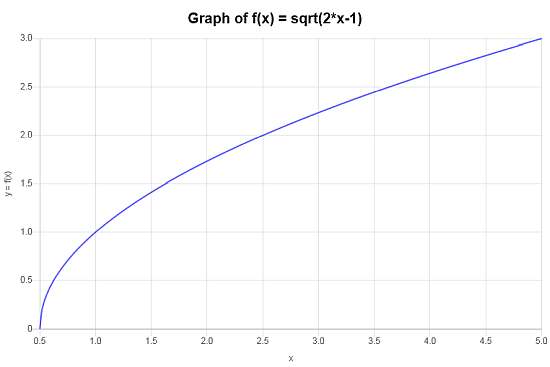
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \sqrt{2x-1} \end{array}\]

No hay nada que simplificar en este caso, y entonces, la función compuesta que buscamos es \(f \circ g(x)=\sqrt{2x-1}\).

Se obtiene el siguiente gráfico para la función compuesta \(f \circ g(x)=\sqrt{2x-1}\) en el intervalo \([-5, 5]\):

Ejemplo: cálculo de función compuesta

Calcular y graficar: \((f \circ g)(x)\) para \(f(x) = x^{3/2}\) y \(g(x) = x+2\). ¿Es \((f \circ g)(x)\) lo mismo que \((g \circ f)(x)\) en este caso?

Solución: Estas son las funciones que necesitamos para componer: \(\displaystyle f(x)=x^{3/2}\) y \(\displaystyle g(x)=x+2\).

Por definición, la función compuesta \(f \circ g\) se define como:

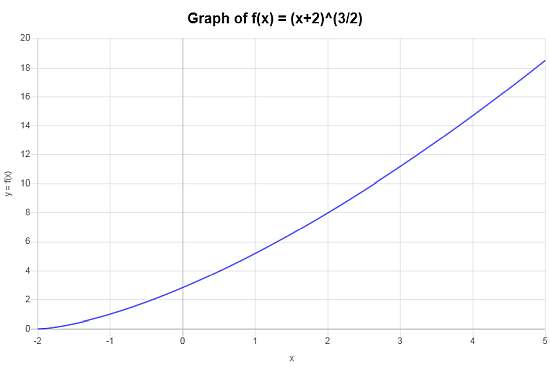
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x+2\right)^{3/2} \end{array}\]

No hay nada que simplificar en este caso, y entonces, la función compuesta que buscamos es \(f \circ g(x)=\left(x+2\right)^{3/2}\).

Se obtiene el siguiente gráfico para la función compuesta \(f \circ g(x)=\left(x+2\right)^{3/2}\) en el intervalo \([-5, 5]\):

Ejemplo: ejemplo de cálculo de función compuesta

Encuentre \((f \circ g)(x)\) para \(f(x) = x^2\) y \(g(x) = x-2\) y grafique la función compuesta.

Solución: En este ejemplo, necesitamos trabajar con \(\displaystyle f(x)=x^2\) y \(\displaystyle g(x)=x-2\), lo que requiere que calculemos la función compuesta. \(f \circ g\).

Usando la definición, la función compuesta \(f \circ g\) se define como:

\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x-2\right)^2 \end{array}\]

La expresión anterior debe simplificarse, y los pasos son los siguientes:

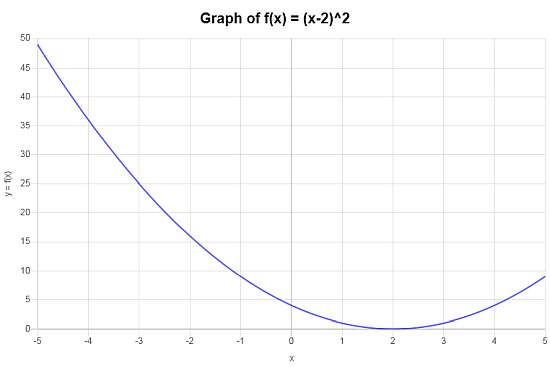
Entonces, después de simplificar, la función compuesta que se obtiene es \(f \circ g(x)=x^2-4x+4\).

La función compuesta \(f \circ g(x)=x^2-4x+4\) conduce a la siguiente gráfica en el intervalo \([-5, 5]\):

Más calculadoras de álgebra

Funciones son uno de los elementos principales en Álgebra y Cálculo. Y la razón de ello es que representa una forma de establecer una relación entre dos variables x e y.

Muchas aplicaciones dependen de las operaciones que realice y también de la gráfica de una función , que contiene toda la información 'almacenada' en la función.