So lösen sie für x

Mit diesem Rechner können Sie für jede beliebige Gleichung, die Sie angeben, eine Lösung für x finden, wobei alle Schritte des Prozesses angezeigt werden, falls eine Lösung gefunden werden kann, was nicht immer der Fall ist.

Sie können einen Ausdruck wie "y = x + 1" angeben, was eine einfache lineare Funktion ist, in der x vorkommt, oder Sie können etwas Komplexeres wie "x^2 + y^2 = 1" angeben, bei dem Sie mehr als eine Lösung haben.

Sobald Sie einen gültigen Ausdruck mit x eingegeben haben, können Sie auf "Berechnen" klicken, um den Prozess zu starten, und der Rechner wird versuchen, x zu lösen, indem er lösen der Gleichung benötigt. Beachten Sie das Wort "Versuch", denn Sie werden feststellen, dass einige Gleichungen nicht gelöst werden können.

Wie lösen sie für x?

Darauf gibt es nicht wirklich eine Antwort, da es stark von der Struktur der Gleichung abhängt, in der x vorkommt. Lineare Gleichungen sind einfach zu handhaben, da es nur darum geht, Begriffe zu verschieben und die Gleichheit gegebenenfalls durch eine Zahl zu dividieren.

Oder für quadratische Gleichungen haben Sie eine einfache Art von Formel, die wohlbekannte quadratische Formel die Ihnen genau sagt, wie Sie x lösen müssen.

Für komplexere Sachverhalte ist es jedoch ein Niemandsland, und jede Gleichung erfordert, wenn überhaupt, einen eigenen Lösungsansatz.

Aus diesem Grund ist eine gleichungsrechner ist deshalb so wichtig, weil es einen Weg zur Lösung der häufigsten Gleichungstypen bietet und darüber hinaus einige Tricks bereithält, die Sie im Falle einer schwierigen Gleichung ausprobieren können, was Ihre Erfolgschancen erhöht.

Schritte zur lösung von x

• Schritt 1: Versuchen Sie zunächst, den Typ der Gleichung zu bestimmen: linear, quadratisch, polynomisch, rational, radikal, logarithmisch, exponentiell usw.
• Schritt 2: Wenn Sie den Typ identifiziert haben, gibt es für diesen speziellen Typ einige spezielle Regeln, die gelöst werden müssen. Beispiel: Wenn Sie feststellen, dass die Gleichung für x eine Exponentialgleichung ist, besteht der übliche Trick für diese Art von Gleichungen darin, eine gemeinsame Basis festzulegen und die Exponenten gleichzusetzen, um die Gleichung zu lösen
• Schritt 3: Wenn keine spezifische Art von Gleichung identifiziert wurde, können Sie einfach einer allgemeinen Art von Fahrplan folgen: Versuchen Sie, alle Terme, die x betreffen, auf einer Seite der Gleichung zu isolieren (je nach Art der Gleichung ist das möglicherweise nicht möglich)
• Schritt 4: Können Sie eine geeignete Substitution anwenden? Können Sie die Dinge vereinfachen, indem Sie eine Funktion oder eine Operation auf beide Seiten der Gleichheit anwenden? Das sind so ziemlich die allgemeinen Ratschläge für den Anfang

Ehrlich gesagt, ist das alles, was man als allgemeine Regel zum Lösen von Gleichungen und zum Lösen von x wissen kann. Der Rest ergibt sich aus der spezifischen Struktur der Gleichung, mit der man zu tun hat.

Es gibt also keine formel für x?

Leider nicht im Allgemeinen. Für die einfacheren Typen können Sie eine Formel für x finden, etwa x = g(y), und manchmal hilft Ihnen diese Formel bei der Definition einer Inverse Funktion aber manchmal findet man keine Formel, und manchmal findet man mehr als eine Lösung.

Manchmal müssen Sie die Variablen einschränken durch lösen einer Ungleichung um eine Lösung für x zu finden. Das heißt, in solchen Fällen ist die Lösung für x nur in einem begrenzten Bereich erfolgreich.

Gibt es einen unterschied zwischen dem lösen nach x und dem lösen nach y?

Ja, unter dem Gesichtspunkt, dass die zu lösende Zielvariable eine andere ist, aber nicht unter methodischen Gesichtspunkten, denn die Schritte, die man zur Lösung von x unternimmt, sind die gleichen, die man zur Lösung von y unternehmen würde.

Das Lösen von x oder y oder z beinhaltet das gleiche Verfahren, nämlich das Lösen einer bestimmten Variablen, was die gleiche Methodik erfordert. Es gibt Fälle, in denen die Symmetrie eine Rolle spielt, und es ist sogar buchstäblich dasselbe. Um es konkret zu sehen: Wenn Sie die Gleichung \(x^2+y^2=1\) haben, würde das Lösen nach x zu genau denselben Schritten führen wie das Lösen nach y. Das gilt aber nur für diese Art von symmetrischen Gleichungen.

Beispiel: lösen sie für x

Finde x in Form von y für : \(\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\)

Lösung: In diesem Fall handelt es sich um eine einfache lineare Gleichung, so dass die Lösung von x nur darin besteht, x auf eine Seite zu setzen:

\[\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y + \frac{5}{6} = \frac{x-1}{x+4}\] \[ \Rightarrow \left( \frac{1}{3} y + \frac{5}{6} \right) (x+4) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} \right) +4 \left( \frac{1}{3} y + \frac{5}{6} \right) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} - 1\right) = - 1 - 4 \left( \frac{1}{3} y + \frac{5}{6} \right)\]

Durch Umstellen der Terme in der obigen Gleichung erhalten wir die Lösung:

\[x=-\frac{2\cdot \left(4y+13\right)}{2y-1} \]

Daher führt die Lösung von \(x\) für die gegebene Gleichung zu der Lösung \(x=-\frac{2\cdot \left(4y+13\right)}{2y-1}\).

Grafisch

Es folgt die grafische Darstellung der mit \(y\) erhaltenen Lösungen in Form von \(\):

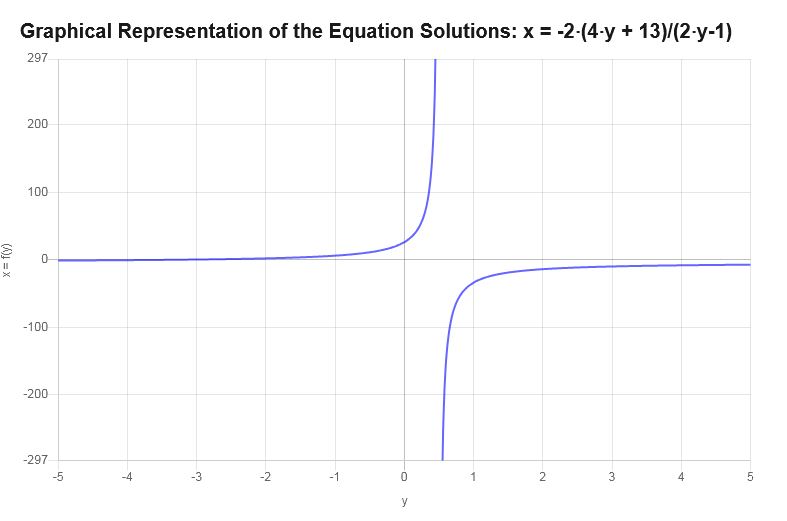
Beispiel: kannst du für x lösen?

Kannst du in diesem Fall für x lösen: \(y = x^2 - 1\)

Lösung: In diesem Fall erhalten wir direkt, dass

\[y = x^2 - 1 \Rightarrow x^2 = y + 1\] \[ \Rightarrow x = \pm \sqrt{ y + 1 }\]

Dies bedeutet, dass wir in der Lage sind, zwei Lösungen oder "Zweige" zu finden, nämlich \(x = \sqrt{ y + 1 }\) und \(x = -\sqrt{ y + 1 }\).

Andere nützliche gleichungsrechner

Wie wir hier gesehen haben, hängt die Lösung von x stark von der Lösen von Gleichungen was bei komplexeren Gleichungen, die keine linearen oder quadratischen Gleichungen sind, durchaus eine Herausforderung sein kann.

Die Idee der Lösung für x ist eng verbunden mit das Inverse finden und auch suche nach dem Graphen der Inversen denn genau damit beginnt man, wenn man mit Inversen zu tun hat.

Gleichungen können komplizierter werden, wenn es sich um simultane Gleichungen handelt, die einige spezielle Techniken erfordern. Ein gängiges Verfahren, mit dem wir umgehen können, ist Lösen von Systemen linearer Gleichungen entweder mit grafischen oder analytischen Methoden