Mehr über den graphen einer inversen funktion

Dieser Rechner hilft Ihnen, den Graphen der von Ihnen angegebenen Umkehrfunktion zu finden, vorausgesetzt, die Funktion hat eine Umkehrfunktion, was nicht immer der Fall ist.

Sie können eine Funktion im Format 'y = 2x - 1' angeben oder einfach einen Ausdruck wie 'f(x) = (x-1)/(x-3)' oder nur '(x-1)/(x-3)', um die Funktion anzugeben.

Sobald Sie eine gültige Funktion angegeben haben, können Sie auf die Schaltfläche "Berechnen" klicken, und es werden alle Schritte der Berechnung angezeigt berechnung der Umkehrfunktion und wenn die Umkehrung existiert, wird ein Graph mit der Funktion und der Umkehrung angezeigt.

Damit die gegebene Funktion eine Umkehrfunktion hat, muss die Funktion eineindeutig sein, d. h. jeder Wert im Bereich der Funktion hat höchstens ein Vorabbild im Bereich der Funktion und genau ein Vorabbild im beschränkten Wirkungsbereich.

Wie man weiß, ob eine funktion invertierbar ist

Bevor man den Graphen der Umkehrfunktion für eine bestimmte Funktion erhält, muss man wissen, ob die Funktion überhaupt eine Umkehrfunktion hat. Das Hauptkriterium für eine Umkehrfunktion ist die Eins-zu-Eins-Beziehung, was bedeutet, dass ein Wert im Bereich nicht zwei zugehörige Werte (Vorbilder) haben kann.

Möglicherweise ziehen es die Schülerinnen und Schüler vor, technische Begriffe wie "Bilder" und "Präimages" nicht zu verwenden. Obwohl es sich dabei um Kernkonzepte der Funktionentheorie handelt, können wir in diesem Fall einen einfachen grafischen Test verwenden, um festzustellen, ob eine Funktion eineindeutig ist oder nicht, und somit, ob man ihre Inverse finden und grafisch darstellen kann.

Horizontaler linientest

Der Horizontallinientest besagt, dass eine Funktion nur dann eineindeutig ist, wenn jede horizontale Linie, die Sie konstruieren, den Graphen der Funktion höchstens einmal schneidet. Wenn Sie eine horizontale Linie finden können, die den Graphen der gegebenen Funktion mehr als einmal kreuzt, dann ist die Funktion NICHT eineindeutig.

Die unten gezeigte Funktion ist beispielsweise eineindeutig, da sie den Graphen der Funktion genau einmal kreuzt, ganz gleich, welche horizontale Linie wir ihr zuweisen:

Aber das nächste Beispiel zeigt eine Funktion, die nicht eins zu eins ist, weil wir eine horizontale Linie sehen, die die Linie der Funktion 2 Mal (mehr als einmal) kreuzt:

Schritte zur ermittlung des inversen graphen

• Schritt 1: Es gibt zwei gängige Methoden: die grafische Methode und die analytische Methode
• Schritt 2: Bei der grafischen Methode müssen Sie zunächst den Horizontallinientest durchführen und sicherstellen, dass er bestanden wird, d. h. dass es sich um eine Eins-zu-Eins-Situation handelt, und dass die Umkehrung existiert
• Schritt 3: Dann zeichnen Sie die Linie y = x in das Diagramm ein (eine Gerade mit einem Winkel von 45 ^o grad in Bezug auf die x-Achse
• Schritt 4: Danach verwendet man einfach die Linie y = x als "Spiegel" und spiegelt die Punkte des ursprünglichen Graphen an dem "Spiegel". Der mit dieser Spiegelung erhaltene Graph ist der Graph der Umkehrung
• Schritt 5: Bei der analytischen Methode müssen Sie zunächst algebraisch den Kehrwert finden : Man beginnt mit y = f(x) und löst dann nach y.
• Schritt 6: Wenn es nur eine Lösung gibt, dann existiert die Umkehrfunktion und man schreibt sie x = g(y). Indem man die Variablennamen anpasst, definiert man formal die inverse Funktion \(f^{-1}\) in Form von g
• Schritt 7: Schließlich stellen Sie die gefundene Umkehrung \(f^{-1}\) grafisch dar, wie Sie es tun würden Grafik eine Funktion normalerweise

Wenn Sie den Graphen einer Umkehrfunktion finden müssen, sind sowohl die grafische als auch die analytische Methode in Ordnung, nur die analytische Methode hat einen Vorteil, nämlich dass Sie die Umkehrfunktion während des Prozesses berechnen, so dass Sie am Ende einen mathematischen Ausdruck dafür haben, nicht nur ihren Graphen.

Warum sollte man den kehrwert graphisch darstellen?

Es gibt so viele Gründe, warum man das tun sollte. Erstens ist die Umkehrfunktion an sich ein sehr wichtiger Akteur in der Funktionentheorie, da eine Funktion zeigt, wie man von einem x zu einem y gelangt. Es ist also nur natürlich, dass man wissen möchte, wie der Mechanismus aussieht, um von y zu x zu gelangen, und genau das liefert einem die Umkehrfunktion.

Man kann sich also eine Funktion als eine Einwegkarte von einem Punkt "X" zu einem Punkt "Y" vorstellen, und die Berechnung der Umkehrfunktion ist wie die explizite Definition einer Karte, die von "Y" nach "X" führt.

Der Graph der Umkehrfunktion gibt Ihnen viele Informationen über die Umkehrfunktion: Geht sie nach unten oder nach oben, wie verhält sie sich?

Wie hilft mir dieser rechner für inverse graphenfunktionen?

Zunächst analysiert dieser Rechner die Funktion, um festzustellen, ob sie mit Hilfe der analytischen Methode invertierbar ist, und wenn es möglich ist, eine solche Inverse zu finden, wird sie für Sie grafisch dargestellt.

Die Suche nach dem Kehrwert umfasst lösen einer Gleichung was keine leichte Aufgabe ist, es sei denn, man hat es mit Lineare Gleichungen oder Polynomgleichungen aber ansonsten kann das Verfahren sehr komplex oder sogar unmöglich sein.

Andere Rechner können einen ähnlichen Prozess durchführen, aber einer der Vorteile von Dieser Taschenrechner ist, dass sie alle Schritte des Prozesses, wenn möglich mit einer detaillierten Erklärung, enthält.

Beispiel: suche nach dem graphen der inversen

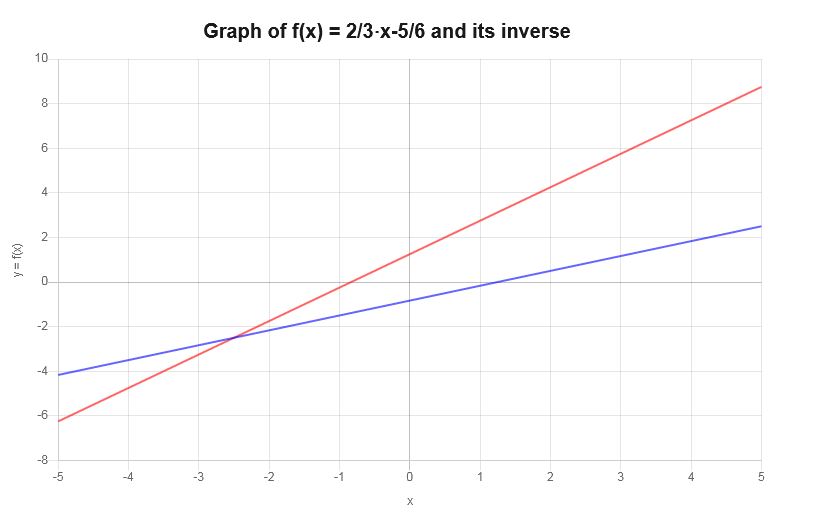
Graphen Sie die Umkehrung von : \( y = \frac{2}{3} x - \frac{5}{6}\)

Lösung:

Die folgende Funktion wurde uns zur Verfügung gestellt:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Um die Umkehrung der gegebenen Funktion zu finden, müssen wir dann \(x\) lösen und feststellen, ob es eine Lösung gibt oder nicht. Die Ausgangsgleichung lautet

\[y=\frac{2}{3}x-\frac{5}{6}\]

Schritt 0: In diesem Fall müssen wir zunächst die gegebene lineare Gleichung vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:

Lösen der linearen gleichung

Setzt man \(x\) auf die linke Seite und \(y\) und die Konstante auf die rechte Seite, erhält man

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Löst man nun \(x\), indem man beide Seiten der Gleichung durch \(-\frac{2}{3}\) dividiert, erhält man folgendes

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

und vereinfachen wir endlich die folgenden

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Daher führt die Lösung von \(y\) für die gegebene lineare Gleichung zu \(x = \frac{3}{2}y+\frac{5}{4}\).

Da wir bei der Lösung von \(x\) eine Lösung finden und es nur eine Lösung gibt, haben wir die Umkehrung gefunden.

Die gefundene umkehrfunktion

Auf der Grundlage der oben gezeigten Arbeit lässt sich schließen, dass die Umkehrfunktion lautet:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

Die Umkehrfunktion kann wie folgt grafisch dargestellt werden:

Beispiel: weitere inverse graphen

Kannst du den inversen Graphen von: \(y = x^2\)

Lösung: Nein, wir können den inversen Graphen von \(y = x^2\) nicht finden, da diese Funktion den Test auf die horizontale Linie nicht besteht. Man kann es auch so sehen, dass wir bei der Lösung von \(x\) \(x = \pm \sqrt y\) erhalten, und da wir zwei Lösungen finden, gibt es keine Umkehrfunktion und folglich auch keinen inversen Graphen.

Weitere funktionsrechner

Funktionen und jede Art von Funktionsoperationen sind das eigentliche Zentrum von Algebra und Calculus. Eine gute Funktionsrechner macht Ihnen das Leben leichter, wenn es darum geht, eine Funktion auf ihren einfachsten Ausdruck zu reduzieren.

Dann haben Sie eine gute funktionsgrafikwerkzeug um einen kurzen Blick auf die grafischen Eigenschaften einer Funktion zu werfen. Ein Blick auf den Graphen einer Funktion kann viel über ihr Verhalten aussagen, noch bevor man ihren algebraischen Ausdruck betrachtet.

Dann gibt es noch fortgeschrittenere Operationen wie die Bestimmung der Ableitung, für die diese Differenzierungsrechner wird sich als nützlich erweisen, da es alle Schritte des Prozesses anzeigt. Wie erwartet hat die Ableitung der Umkehrfunktion einen interessanten Zusammenhang mit der Ableitung der ursprünglichen Funktion.