Verwenden der descartes -regel von zeichen

Dieser Taschenrechner hilft Ihnen bei der Anwendung der Descartes -Regel von Zeichen für ein bestimmtes Polynom, das Sie bereitstellen.Die einzige Voraussetzung dafür ist, dass das Polynom gültig sein muss.

Zum Beispiel können Sie einfaches kubisches Polynom wie x^3 - 2x + 1 bereitstellen, aber Sie können auch eine kompliziertere Bereitstellung wie x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^2 + 2x + 1 usw.

Sobald Sie eine gültige bereitstellen Polynomfungion Sie klicken auf die Schaltfläche "Berechnen", um alle Schritte des angezeigten Vorgangs zu erhalten.

Funde von Polynomnullen ist eine der wichtigsten Aufgaben in der Algebra, aber es ist im Allgemeinen keine leichte Aufgabe.Es gibt keine allgemeinen Formeln für alle Polynome aller Grade, daher müssen wir normalerweise ein systematisches Verfahren befolgen, um so viele Wurzeln wie möglich zu finden.

In diesem Zusammenhang ist es immer nützlich, so viele Informationen über die Art der verfügbaren Wurzeln zu haben, und das sind die Ziele der Descartes -Regel von Zeichen.

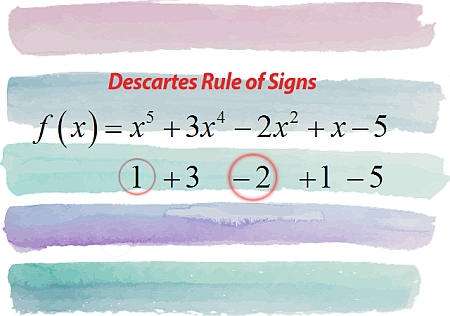
Was gibt die descartes -regel der zeichen an?

In einfachen Worten, die Descartes -Regel der Zeichen der Zeichen erzählen Ihnen etwas über die Anzahl der positiven und negativen Wurzeln eines Polynoms, indem Sie nur die Zeichen der Koeffizienten des gegebenen Polynoms betrachten.

Genauer gesagt beginnen Sie mit dem führenden Koeffizienten, ignorieren Nullkoeffizienten und zählen Änderungen des Zeichens.Die Gesamtzahl der Änderungen im Vorzeichen aufeinanderfolgenden Koeffizienten ist eine Obergrenze für die Anzahl der positiven Wurzeln von \(p(x)\) und die Anzahl der positiven Wurzeln hat die gleiche Parität wie die Gesamtzahl der Änderungen der Zeichen.

Dann machen Sie dieselbe Übung, aber für die Koeffizienten von \(p(-x)\) und in diesem Fall ist die Gesamtzahl der Änderungen im Vorzeichen aufeinanderfolgenden Koeffizienten eine Obergrenze für die Anzahl der negativen Wurzeln von \(p(x)\) und die Anzahl der Negativen Wurzeln hat die gleiche Parität wie die Gesamtzahl der Vorzeichenänderungen.

Schritte zur anwendung von descartes -regel von zeichen der zeichen

• Schritt 1: Identifizieren Sie das Polynom P (x), das Sie analysieren müssen.Stellen Sie sicher, dass es sich um ein Polynom handelt (ansonsten funktioniert die Methode nicht) und vereinfachen Sie es so weit wie möglich
• Schritt 2: Setzen Sie die Koeffizienten von P (x) in eine Reihe aus, beginnend mit dem führenden Koeffizienten, in absteigender Reihenfolge und weglassen Nullkoeffizienten
• Schritt 3: Zählen Sie aus dem führenden Koeffizienten die Vorzeichenänderungen zwischen aufeinanderfolgenden Koeffizienten und beachten Sie die Gesamtzahl der Zeichenänderungen und nennen Sie es t
• Schritt 4: Die Anzahl der positiven Nullen von P (x) ist höchstens t und hat die gleiche Parität wie T (wenn t gerade ist, dann ist die Anzahl der positiven Nullen von P (x) eine gleichmäßige Zahl, und wenn t ungerad ist, ist er ungerade.Dann ist die Anzahl der positiven Nullen von P (x) eine ungerade Zahl)
• Schritt 4: Wiederholen Sie den gleichen Vorgang jetzt für die Koeffizienten von P (-x), um Informationen über die Anzahl der negativen Nullen von P (x) zu erhalten.

Diese Methode kann Ihnen potenziell einen Bereich möglicher Werte für die Anzahl der positiven (und negativen) Nullen geben, aber sie kann Ihnen jedoch auch genau sagendu zählst.

Kann ich die tatsächlichen nullen mit dieser methode berechnen?

Nein, Descartes -Regel der Zeichen soll Ihnen nicht Informationen darüber geben, was die tatsächlichen Wurzeln sind. Sie erzählt Ihnen nur etwas über die Anzahl der positiven (und negativen) Wurzeln.

Nun diese Informationen mit dem kombinieren, mit dem Rationaler Wurzel Theorem und andere elementare Werkzeuge, einschließlich Synthetische Abteilung und die Faktorsatz Sie sind besser für den tatsächlichen Wert der Wurzeln gerüstet.

Tipps und tricks

Stets Vereinfachen das Polynom zuerst.Wenn Sie beispielsweise \(p(x) = x^5 - x^3\) haben, möchten Sie zunächst \(p(x) = x^5 - x^3 = x^3(x^2 - 1)\), also wissen Sie, dass 0 eine Wurzel ist (mit Multiplizität 3), und Sie wenden Descartes -Regel auf \(x^2 - 1\) anstattdessen.

Beispiel: descartes -regel der zeichen

Geben Sie die mögliche Anzahl positiver und negativer Wurzeln von \(x^4 - x^3 + x^2 + 1\) an

Lösung: Wir erhalten die folgende Polynomfunktion: \(\displaystyle x^4 - x^3 + x^2 + 1\), für die wir die Descartes -Regel von Zeichen anwenden müssen.

Positiver Wurzeln : Die Polynomkoeffizienten (für höher bis niedrigere Leistung) sind:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

Wir stellen fest, dass die Anzahl der Zeichenänderungen in aufeinanderfolgenden Koeffizienten: \(2\) lautet, und die Änderungen sind: \(\,\,+1\,\,\) und \(\,\,-1\,\,\), \(\,\,-1\,\,\) und \(\,\,+1\,\,\).

Negatives Wurzeln : Die Polynomkoeffizienten für \(p(-x) = x^4+x^3+x^2+1\) sind:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

Für die Koeffizienten von \(p(-x)\) werden keine Zeichenänderungen gefunden.

Fazit: Basierend auf der Anzahl der gefundenen Zeichenänderungen, die \(2\) sind, schließen wir, dass \(p(x)\) 0 oder 2 positive Wurzeln für \(p(x) = x^4-x^3+x^2+1\) haben kann.

Da für die Koeffizienten von \(p(-x)\) nun keine Zeichenänderungen gefunden wurden, schließen wir, dass es keine negativen Nullen für \(p(x) = x^4-x^3+x^2+1\) gibt.

Beispiel: mehr descartes -zeichenregel

Geben Sie die mögliche Anzahl positiver und negativer Wurzeln von \(x^4 + x^3 + x^2 - 1\) an

Lösung: Jetzt müssen wir \(\displaystyle x^4 + x^3 + x^2 - 1\) mit Descartes -Regel von Zeichen analysieren.

Der bereitgestellte Ausdruck ist bereits vereinfacht, daher gibt es nichts weiter zu vereinfachen.

Positiver Wurzeln : Die Koeffizienten sind:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

Beachten Sie, dass die Anzahl der Vorzeichenänderungen in aufeinanderfolgenden Koeffizienten in diesem Fall gleich \(1\) entspricht, und die Änderungen sind: \(\,\,+1\,\,\) und \(\,\,-1\,\,\).

Negatives Wurzeln : Die Polynomkoeffizienten, die \(p(-x) = x^4-x^3+x^2-1\) zugeordnet sind, sind:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

Anschließend ist die Anzahl der Vorzeichenänderungen in aufeinanderfolgenden Koeffizienten gleich zu \(3\) und die Änderungen sind: \(\,\,+1\,\,\) und \(\,\,-1\,\,\), \(\,\,-1\,\,\) und \(\,\,+1\,\,\), <<, \(\,\,+1\,\,\) und \(\,\,-1\,\,\)

Fazit: Da es eine Vorzeichenänderung zwischen den Koeffizienten von \(p(x)\) gibt, schließen wir, dass es genau eine positive Null für \(p(x) = x^4+x^3+x^2-1\) gibt.

Basierend auf der Anzahl der gefundenen Zeichenänderungen, die \(3\) sind, schließen wir, dass \(p(x) = x^4+x^3+x^2-1\) 1 oder 3 negative Wurzeln haben kann.

Beispiel: positive und negative vorzeichen

Geben Sie die mögliche Anzahl positiver und negativer Wurzeln von \(x^4 + 1\) an.Können Sie etwas sagen, die genaue Anzahl positiver und negativer Wurzeln?

Lösung: In diesem Fall gibt es keine Zeichenänderungen, also gibt es keine positiven Wurzeln.Nun, \(p(-x) = (-x)^4 + 1 = x^4 + 1\), was keine Zeichenänderungen hat, also gibt es auch keine negativen Wurzeln.Die Schlussfolgerung ist, dass Polynom keine echten Wurzeln hat (da 0 auch keine Wurzel ist).

Mehr polynomrechner

Polynomwurzeln Funde ist eine der zentralen Punkte für die meisten Anwendungsprobleme in Kalkül und Algebra, und es ist eine Fähigkeit, die es wert ist, gemeistert zu werden.

Es gibt viele Fähigkeiten bei der Berechnung von Nullen eines Polynoms und Descartes Zeichen Regel Gibt Ihnen viele Informationen, die einfach nur durch Betrachtung der Koeffizienten des Polynoms abgeleitet werden können.