Prueba de línea horizontal

Esta calculadora le permitirá ejecutar la prueba de línea horizontal para cualquier función que proporcione, mostrando los pasos. La función que proporcione podría ser algo así como 'y = 2x - 1', que es el tipo más simple de función lineal puede encontrar, o puede proporcionar una función más compleja como 'y = (2x-1)/(x+1)' que involucra una función racional .

Una vez que proporcione una función válida, puede hacer clic en el botón "Calcular" y se le proporcionarán todos los pasos del proceso, indicando si la función pasa o no la prueba de línea horizontal (HLT).

La forma en que funciona esta calculadora es estableciendo una línea horizontal genérica y verificando cuántas veces (si es que alguna vez lo hace) la línea cruza esta línea horizontal arbitraria dada. Esto implica Resolviendo para x la ecuación y = f(x).

¿qué es la prueba de la línea horizontal?

El HLT es una prueba que permite evaluar si una función es uno a uno o no. Consiste en dibujar líneas horizontales a diferentes alturas y ver dónde se cruzan con la gráfica de la función dada f(x), si es que lo hacen.

Si ninguna línea horizontal que puedas imaginar cruce la gráfica de la función f(x) más de una vez, entonces la función es uno a uno . Por otro lado, si eres capaz de encontrar una línea horizontal que cruce la gráfica de la función f(x) MÁS DE UNA VEZ, entonces has demostrado que la función NO es uno a uno

Entonces quizás estés pensando "Espera un momento", esta herramienta no funciona realmente para demostrar que una función es uno a uno usando la prueba de la línea horizontal, sino más bien para demostrar que NO ES uno a uno usándola. .

Porque, en la práctica, no puedo graficar TODAS las líneas horizontales que hay para comprobar cuántas veces cruzan la gráfica de f(x), pero si encuentro UNA línea horizontal que cruza la gráfica de f(x) demasiadas veces, entonces sé que no es uno a uno. Entonces, bien pensado, has encontrado algo bueno allí.

Uso práctico de la prueba de la línea horizontal

Por ejemplo, si tienes la función \(f(x) = x^2\), entonces la gráfica se vería más o menos así:

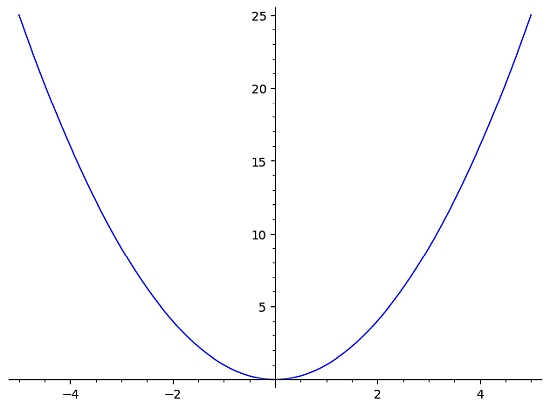
En este caso, vemos de inmediato que esta función no pasa la prueba de la línea horizontal. Por qué, porque la línea horizontal y = 10 que se muestra en el siguiente gráfico cruza la gráfica de f(x) dos veces (más de una vez)

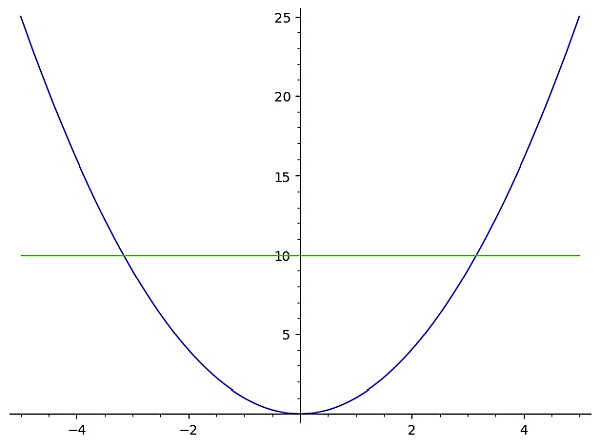
En este caso, la función \(f(x) = x^2\) no pasa la prueba de la línea horizontal y por lo tanto, no es una función uno a uno .

Ahora, dado que es imposible probar TODAS las líneas horizontales posibles, el HLT debe intentar utilizar medios algebraicos, a menos que vea visualmente un caso claro de una línea horizontal que hará que la función no pase la prueba.

Uso de la prueba de la línea horizontal (analíticamente)

• Paso 1: Comience con una función válida dada f(x), establecerá el nivel de una línea horizontal en un valor arbitrario de y
• Paso 2: Entonces estableces la ecuación: y = f(x), y el objetivo es resolver para x
• Paso 3: No existe una sola estrategia para resuelve esta ecuación , ya que depende de la naturaleza de la función f(x). Si f(x) es una función lineal o cuadrática simple, entonces es bastante fácil resolver x. Si no es así, entonces es necesario probar diferentes métodos
• Etapa 4: Si al resolver x encuentras más de una solución para una y arbitraria, entonces la función falla el HLT. De lo contrario, si hay una solución o ninguna, la pasa.

La resta de fracciones se deriva simplemente de la suma de fracciones: Para restar dos fracciones, simplemente multiplicas la segunda por -1 y luego la sumas a la primera. .

¿la recta horizontal puede tomar valores negativos o positivos?

La clave principal de la implementación analítica del HLT es que se elige una línea horizontal arbitraria. Puede ser un valor arbitrario, ya sea positivo o negativo. Entonces, el valor arbitrario de y utilizado PUEDE determinar si las soluciones propuestas están bien definidas o no, pero eso no AGREGA más soluciones, sino que potencialmente puede restar soluciones.

Por ejemplo, cuando comienzas con \(f(x)= \frac{2x+1}{x-1}\) y resuelves para x esto: \(y = \frac{2x+1}{x-1}\), obtendrás

\(x = \frac{y+1}{y-2}\)

lo que significa que para un \(y\) determinado tienes COMO MÁXIMO una solución. ¿Por qué una solución como máximo? Porque cuando y = 2 en realidad no hay solución, y para cualquier otro y, hay una solución. Esto funciona muy bien para demostrar que la función pasa la prueba de la línea horizontal.

Ejemplo: aprobar el hlt

¿La siguiente función pasa el HLT: \(f(x) = \frac{1}{3} x + \frac{5}{4}\)?

Solución:

La función que se ha proporcionado es:

\[f\left(x\right) = \frac13x+\frac54\]

Luego, para evaluar si la función dada pasa o no la prueba de la línea horizontal, necesitamos resolver \(x\) y determinar si no hay solución, hay una solución o múltiples soluciones. La ecuación inicial es

\[y=\frac{1}{3}x+\frac{5}{4}\]

Resolver la ecuación lineal

Poniendo \(x\) en el lado izquierdo y \(y\) y la constante en el lado derecho obtenemos

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

Ahora, resolviendo \(x\), al dividir ambos lados de la ecuación entre \(-\frac{1}{3}\), se obtiene lo siguiente

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

y simplificando obtenemos finalmente lo siguiente

\[\displaystyle x=3y-\frac{15}{4}\]

Por lo tanto, resolver \(x\) para una ecuación lineal dada conduce a \(x = 3y-\frac{15}{4}\).

Encontramos que dado que al resolver para \(x\) encontramos una solución y es solo una solución, la función dada pasa la prueba de la línea horizontal.

Los resultados de la prueba de la línea horizontal

Con base en el trabajo mostrado arriba, se puede concluir que la función dada pasa la prueba de la línea horizontal.

Gráficamente la situación se representa de la siguiente manera:

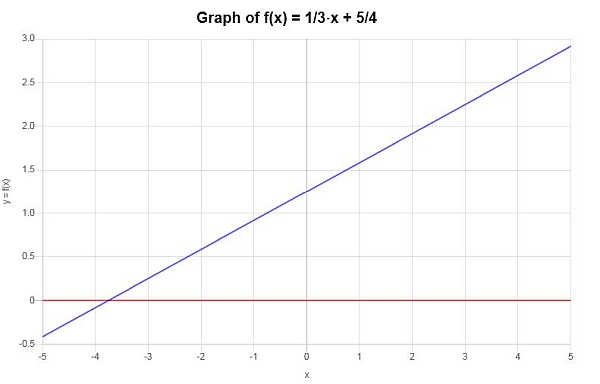
Ejemplo: ¿esta función es uno a uno?

Usando la prueba de la línea horizontal, indique si la siguiente función es uno a uno: \(f(x) = x^3 - 1\)

Solución: Para evaluar si la función dada pasa o no la prueba de la línea horizontal, necesitamos resolver la ecuación \(y = x^3 - 1\) para \(x\) y determinar si no hay solución, hay una solución o múltiples soluciones.

Paso Inicial: En este caso, primero necesitamos simplificar la ecuación dada y, para hacerlo, llevamos a cabo los siguientes pasos de simplificación:

Luego obtenemos las soluciones:

\[x_1=\left(y+1\right)^{\frac{1}{3}} \] \[x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right) \] \[x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right) \]

De estas soluciones, solo tenemos una solución real, que es \(x_1=\left(y+1\right)^{\frac{1}{3}}\). Por lo tanto, y dado que al resolver para \(x\) encontramos una solución y es solo una solución real, la función dada pasa la prueba de la recta horizontal.