Más sobre funciones lineales

Esta calculadora de función lineal le permitirá calcular una función lineal proporcionando cierta información requerida sobre la función.

Hay varias formas de hacerlo. Puede (1) proporcionar una ecuación lineal en x e y que se pueda resolver para y, o (2) proporcionar directamente la Pendiente y Y-Intercept , o (3) puede proporcionar la pendiente y un punto por donde pasa la línea, o (4) puede proporcionar 2 puntos por donde pasa la línea.

¿Qué información proporcionará? Dependerá en gran medida de la información que tengas disponible, y dependerá del caso específico.

Un caso común es encontrar una función lineal que pase por dos puntos dados, pero las otras formas de determinar la línea también son comunes.

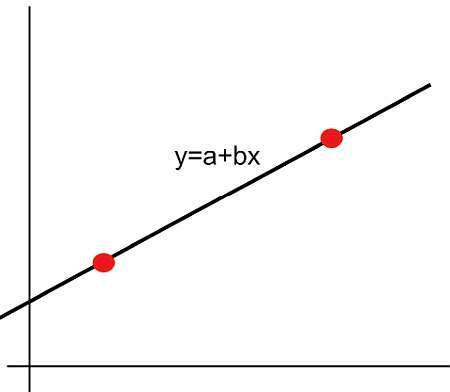
¿qué es una función lineal?

La respuesta depende de cuántas variables esté considerando, pero para una variable x, una función lineal es una función de la forma

\[f(x) = a + b x \]

Solo un tecnicismo, en matemáticas más avanzadas, esta es una función afín lineal, y no es estrictamente lineal a menos que a = 0, pero esa idea va más allá del alcance de esta presentación. Para nosotros, \(f(x) = a + b x \) es una función lineal en x.

El valor de a en \(f(x) = a + b x \) se conoce como Y-Intercept , y b se conoce como Pendiente . A veces verás la convención \(f(x) = mx + n \), donde m es la pendiente y n es la intersección con el eje y.

Pero esa es una convención de nombres, solo necesitas recordar que la constante que multiplica la variable x es la pendiente, y la otra es el intercepto en y. ¿Porqué es eso? Porque cuando x = 0, obtenemos \(f(0) = m \cdot 0 + n = n\), lo que indica que n es precisamente el intercepto por qué.

¿cuáles son los pasos para calcular una función lineal?

• Paso 1: Identifique qué tipo de información ha proporcionado
• Paso 2: si la información que tiene es una ecuación lineal en x e y, necesita resolver para y y luego automáticamente tiene la función lineal configurando f(x) = y
• Paso 3: si tienes la pendiente b y el intercepto en y a, entonces la función lineal es directamente f(x) = a + b x
• Paso 5: si tiene dos puntos \((x_1, y_1)\) y \((x_2, y_2)\) por donde pasa la línea, entonces puede usar la fórmula: \(\displaystyle f(x) = y_1 + \left(\frac{y_2-y_1}{x_2-x_1} \right)(x-x_1)\) para la función lineal
• Paso 6: Si en cambio tiene un punto \((x_1, y_1)\) por donde pasa la línea y la pendiente, entonces puede usar la fórmula: \(\displaystyle f(x) = y_1 + m(x-x_1)\) para la función lineal

La lista anterior de pasos es una lista completa y considera todos los casos posibles. Ultimate, la situación más simple y menos complicada corresponde al caso en el que se conocen la pendiente y el intercepto en y, donde podemos calcular la forma de intercepción de la pendiente inmediatamente, pero no siempre es así.

¿cuál es la fórmula de la función lineal?

En última instancia, e independientemente de la información que hayas proporcionado, puedes llegar a la fórmula de la función lineal conocida como forma pendiente-intersección, que es:

\[y = a + bx \]

Ahora, ya que estás definiendo una función, también puedes escribir \(f(x) = a + b x\).

¿cuáles son los pasos para encontrar la fórmula de la función lineal?

• Paso 1: Identifique la información proporcionada
• Paso 2: llegar a la fórmula correspondiente y = a + bx, identificando la pendiente b y el intercepto en y a
• Paso 3: Reemplace y por f(x) y escriba f(x) = a + bx

Geométricamente, el gráfico de función lineal será una línea que realmente cruza el eje y en el punto (0, a), y la pendiente b reflejará el grado de inclinación de la línea.

¿por qué es útil calcular funciones lineales?

La relación lineal entre variables es muy común en tantas aplicaciones, por lo que se vuelve indispensable entender completamente cómo funcionan las funciones lineales.

Y también podemos definir funciones lineales para más variables, lo que las convierte en un objeto aún más poderoso.

Ejemplo: calculadora de funciones lineales

Calcula la ecuación de la función lineal que pasa por los puntos: \( (\frac{22}{3}, \frac{7}{4})\) y \((-1, \frac{5}{6})\)

Solución: El objetivo principal es construir una función lineal basada en la información proporcionada, si es posible.

La información proporcionada sobre la recta es que ésta pasa por los puntos\(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\) y \(\displaystyle \left( -1, \frac{5}{6}\right)\)

Por lo tanto, el primer paso consiste en calcular la pendiente. La fórmula de la pendiente es \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Ahora, enchufando los números correspondientes es , obtenemos que la pendiente es: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{5}{6} - \frac{7}{4}}{ \displaystyle -1 - \frac{22}{3}} = \frac{ \displaystyle \frac{5}{6}-\frac{7}{4}}{ \displaystyle -1-\frac{22}{3}} = \frac{11}{100}\]

Entonces, ahora sabemos que la pendiente es \(\displaystyle m = \frac{11}{100}\) y que la recta pasa por el punto \(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\)

Por lo tanto, con la información que tenemos, podemos construir directamente la forma punto-pendiente de la línea, que es

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

y, a continuación, insertando los valores conocidos de \(\displaystyle b = \frac{11}{100}\) y \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{22}{3}, \frac{7}{4}\right)\), obtenemos que

\[\displaystyle y-\frac{7}{4} = \frac{11}{100} \left(x-\frac{22}{3}\right)\]

Ahora, tenemos que expandir el lado derecho de la ecuación distribuyendo la pendiente, por lo que obtenemos \[\displaystyle y = \frac{11}{100} x + \frac{11}{100} \left(-\frac{22}{3}\right) + \frac{7}{4}\]

y simplificando obtenemos que \[\displaystyle y=\frac{11}{100}x+\frac{283}{300}\]

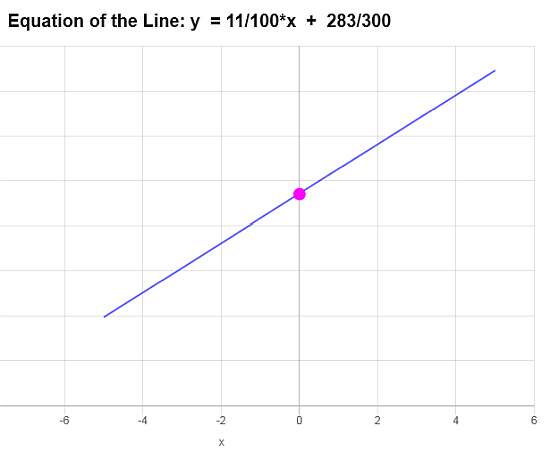
Conclusión : Con base en los datos provistos, concluimos que la ecuación de la línea es \(\displaystyle f(x)=\frac{11}{100}x+\frac{283}{300}\), y corresponde a una línea con una pendiente de \(\displaystyle b = \frac{11}{100}\) y una intersección con el eje y de \(\displaystyle a = \frac{283}{300}\).

En base a esta información, el gráfico es:

Ejemplo: otro cálculo de función lineal

Calcular la función lineal asociada a : \(\frac{1}{3}x + \frac{5}{4}y - \frac{5}{6} = 0\)

Solución:

Ahora, para este ejemplo, la forma en que hemos definido una función lineal es a través de una ecuación lineal general, dada por:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Podemos simplificar constantes:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Ahora, poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Ahora, resolviendo para \(y\), dividiendo ambos lados de la ecuación por \(\frac{5}{4}\), se obtiene lo siguiente

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{5}{6}}{\frac{5}{4}}\]

y simplificando obtenemos finalmente lo siguiente

\[\displaystyle y=-\frac{4}{15}x+\frac{2}{3}\]

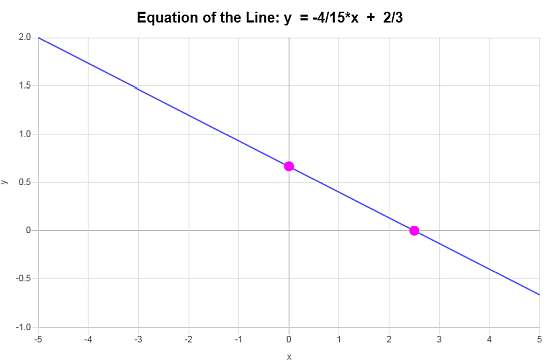
Conclusión : Ahora podemos decir que en base a los datos proporcionados, la conclusión es que la ecuación de la línea es \(\displaystyle f(x)=-\frac{4}{15}x+\frac{2}{3}\), y corresponde a una línea con una pendiente de \(\displaystyle b = -\frac{4}{15}\) y una intersección en y de < >.

En base a esta información, el gráfico es:

Ejemplo: más calculadoras de funciones lineales

Calcula la función lineal con pendiente m = 0 y que cruza el eje y en el punto (0, 4).

Solución: En este caso, hemos dado la pendiente, que es m = 0, y el intercepto en y, que es (0, 4). Dado que la pendiente es 0, la línea es horizontal, por lo que en este caso, la ecuación de la línea es \(f(x) = 4\).

Más calculadoras de funciones lineales

Las calculadoras interesantes son la calculadora de pendiente y la calculadora de intercepción en y. También te puede interesar encontrar la recta perpendicular a una recta dada .

Otra forma común para la línea es la formulario estándar , y puede convertir ciertos de una forma a la otra.