Funciones uno a uno

Esta calculadora te permitirá valorar si una función es uno a uno, mostrándote todos los pasos. Lo primero que debe hacer es proporcionar la función. Esto podría ser algo simple, lineal o cuadrático como 'y = x^2 - 1', o podrías decidir optar por un función racional como 'f(x) = (x-1)/(x+3)'.

Luego, cuando esté satisfecho con lo que ha proporcionado y se haya asegurado de que la función sea válida, haga clic en el botón "Calcular" para que se le muestren todos los pasos del proceso.

El concepto de función uno a uno es muy importante en Álgebra y Cálculo. Hay muchas formas sencillas de realizar pruebas uno a uno, una de ellas es la Prueba de línea horizontal , pero debido a su naturaleza, es más fácil de usar para refutar que una función sea uno a uno. Para demostrar que una función es uno a uno, necesitamos un resolución de ecuaciones , proceso analítico.

¿qué es un proceso uno a uno?

En pocas palabras, una función uno a uno o inyectiva es aquella en la que para dos \(x_1\) y \(x_2\) diferentes, los valores de sus imágenes a través de \(f(x)\) son diferentes, lo que significa matemáticamente

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

A algunos profesores les gusta escribirlo de manera ligeramente diferente, pero aún así de manera equivalente: La función es uno a uno si

\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]

Esto quiere decir de una manera bastante sofisticada que, si la gráfica de la función cruza el mismo valor (una línea horizontal), eso sucede sólo cuando el punto es el mismo. Entonces, todo lo que estás diciendo es que no hay dos puntos diferentes donde lo cruce una línea horizontal. Entonces, simplemente estás reiterando el Prueba de línea horizontal .

Cómo comprobar si una función es uno a uno o no

• Paso 1: Comience con la función original f(x) y establezca la ecuación y = f(x)
• Paso 2: Intenta resolver para x
• Paso 3: Si encuentra más de una solución, entonces la función NO es uno a uno, y si tiene una solución o ninguna, entonces la función es uno a uno

Normalmente, realizará una inspección básica para asegurarse de que esa función claramente no sea uno a uno, posiblemente porque puede encontrar fácilmente una línea horizontal que haga que el HLT falle.

Luego, buscará algunas propiedades visuales básicas: ¿La función siempre es creciente (entonces es uno a uno), y lo mismo ocurre en el caso en que la función siempre es decreciente?

¿cómo se relaciona uno a uno con encontrar la inversa?

Dicho en términos simples, para encontrar la inversa de una función, la función DEBE ser uno a uno, al menos en un determinado subdominio. Muchas veces restringimos el dominio, por lo que hacemos una función 1 a 1 en un dominio restringido, que de otra manera no sería 1 a 1.

Por ejemplo, \(f(x) = x^2\) no es uno a uno en general. Porque puedes tomar dos puntos diferentes \(x_1 = -1\) y \(x_2 = 1\) y encontrar que \(f(x_1) = (-1)^2 = 1\) y \(f(1) = 1^2 = 1\), lo que significa que la propiedad (la caracterización uno a uno)

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

no está satisfecho. Ahora, si en lugar de considerar la recta real completa \(\R\), consideramos solo los valores positivos, podemos concluir que la función es uno a uno sobre los valores reales positivos (Pista: En ese subdominio, la función es creciente)

¿existe una fórmula para evaluar si una función es uno a uno?

Lamentablemente no. Quiero decir, uno podría pensar en \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \), como la fórmula uno a uno, pero esto es más una condición lógica que una fórmula.

Sin embargo, existe un procedimiento genérico muy amplio que se utiliza para probar si una función es uno a uno o no, que es lo que se explica anteriormente. No existe una "fórmula uno a uno". Si tuviéramos que conformarnos con uno, debería ser y = f(x).

Y simplemente resolvemos para x. Nada más y nada menos. En última instancia, dependerá de qué se trata f(x). Una función muy compleja y complicada puede plantear muchas dificultades para resolverla, y tal vez necesites una calculadora de funciones para ello, e incluso con una calculadora de funciones puedes fallar.

Probablemente estés pensando, ¿por qué es eso? Es porque, en el fondo, no tenemos técnicas para resolver TODAS las ecuaciones. Simplemente hacemos lo que podemos con algún tipo específico de ecuaciones, pero estamos muy lejos de conocer una forma EXACTA de resolver todas las ecuaciones.

Ejemplo: función uno a uno

¿La siguiente función es inyectiva: \(f(x) = \frac{1}{4} x + \frac{5}{4}\)

Solución:

Se nos ha proporcionado la siguiente función:

\[f(x) = \frac{1}{4} x + \frac{5}{4}\]

Luego, para evaluar si la función dada es uno a uno, necesitamos resolver \(x\) y determinar si no hay solución, una solución o múltiples soluciones. La ecuación inicial es

\[y=\frac{1}{4}x+\frac{5}{4}\]

Poniendo \(x\) en el lado izquierdo y \(y\) y la constante en el lado derecho obtenemos

\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]

Ahora, resolviendo \(x\), al dividir ambos lados de la ecuación entre \(-\frac{1}{4}\), se obtiene lo siguiente

\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]

y simplificando obtenemos finalmente lo siguiente

\[\displaystyle x=4y-5\]

Por lo tanto, resolver \(x\) para una ecuación lineal dada conduce a \(x=4y-5\) y es solo una solución real, por lo que la función dada es uno a uno.

Conclusión

Con base en lo encontrado en la sección anterior, se puede concluir que la función dada es uno a uno.

Gráficamente:

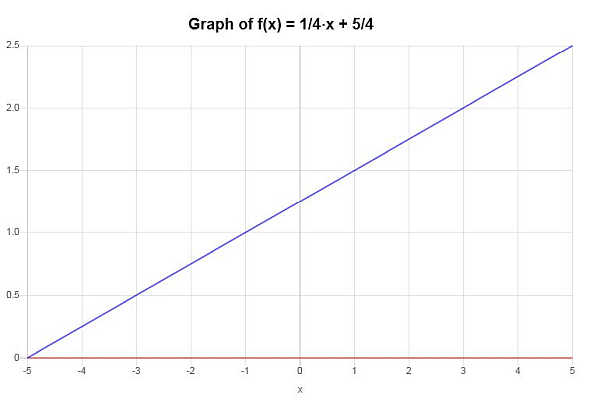
Ejemplo: función 1 a 1

Demuestre o refute que la siguiente función es uno a uno: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)

Solución: Para evaluar si la función dada es uno a uno, necesitamos resolver \(x\) y determinar si no hay solución, una solución o múltiples soluciones. La ecuación inicial que debemos usar es:

\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]

Paso Inicial: En este caso, primero necesitamos simplificar la ecuación dada y, para hacerlo, llevamos a cabo los siguientes pasos de simplificación:

Entonces, las soluciones son:

\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]

Estado uno a uno

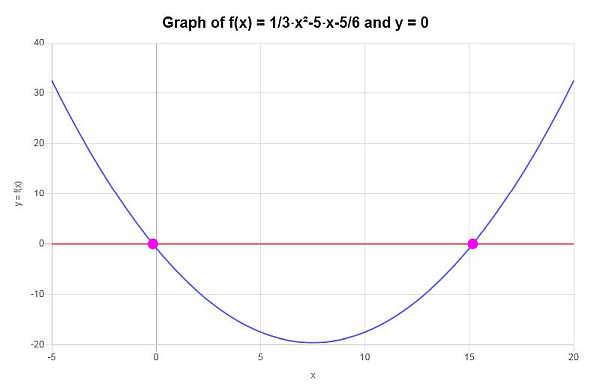
Con base en el trabajo mostrado arriba se puede concluir que la función dada NO ES UNO A UNO, ya que no pasa la Prueba de la Línea Horizontal, como por ejemplo la línea \(y = 0\) es una línea horizontal que cruza la función dada mas de una vez.

Gráficamente la situación se representa de la siguiente manera:

Calculadoras de álgebra más interesantes

El concepto de funciones 1 a 1 normalmente se da por sentado, pero es muy importante, crítico diría yo. Esto se debe a que el concepto de uno a uno está estrechamente relacionado con la idea de función monótona (funciones crecientes o decrecientes), al mismo tiempo que está estrechamente relacionado con la cálculo de la función inversa y su gráfica.

Sin embargo, muchas veces es difícil atravesar el bosque más allá de los árboles, ya que los conceptos más importantes de álgebra y cálculo tienen estrechos vínculos entre sí. Análisis de funciones es una de las cosas que harás todo el tiempo, por lo que es bueno adquirir las habilidades para ser bueno en eso.