Calculadora de función inversa
Instrucciones: Utilice esta calculadora para encontrar la función inversa de una función que proporcione y muestre todos los pasos. Escriba la expresión de función para la que desea encontrar la inversa en el cuadro a continuación.
Más sobre esta calculadora de función inversa
Esta calculadora te permitirá encontrar la inversa de una función determinada mostrando todos los pasos, asumiendo que la inversa existe. La calculadora examinará la función resolver una ecuación asociado a la definición de la función, e intentará valorar si existe o no una inversa.
Por ejemplo, puedes proporcionar una función lineal como 'f(x) = 3x - 2', que sería un caso simple, o por ejemplo podrías llevarlo a un nivel superior con algo un poco más difícil, como con una función racional como 'y = (x-1)/(x-3)'.
Una vez que proporcione una función válida, haga clic en el botón "Calcular" para que se le muestren todos los pasos del proceso, con la función inversa como respuesta final, si existe una inversa, o con la explicación de que no se pudo encontrar ninguna solución. y por qué.
No se garantiza que encontrará todas las funciones inversas. Por un lado, no todas las funciones tienen una inversa y, por otro, (como veremos en la siguiente sección), el proceso de encontrar la inversa implica Resolviendo para x para una ecuación y, como sabemos, algunas ecuaciones pueden ser muy difíciles o imposibles de resolver.
Entonces, es más probable que las funciones más simples sean capaces de encontrar su inversa, en caso de que exista la inversa.

¿cómo se define la inversa de una función?
En términos sencillos, la inversa de una función es la función que hace lo contrario de lo que hace la función original. Entonces, piensa en una función en términos de y = f(x), y luego podrías pensar en ella a medida que avanzas de x a y. Alimentas la función con una x, y la función te da una y específica.
La función inversa comienza con y y encuentra el camino de regreso a x, de manera que x es la misma que llevó a y a través de la función original. Ahora, la definición formal se hace a través de composición de funciones . Para una función \(f\), decimos que \(g\) es la función inversa de \(f\) si
\[ f(g(x)) = x \]y
\[ g(f(x)) = x \]para todo x en un determinado conjunto. Hay más, pero lo dejaremos en el nivel intuitivo (Estrictamente hablando, una función necesita ser inyectiva y sobreyectiva para ser invertible, y algunos otros tecnicismos que se están considerando, como restringir la dominio y rango , etc.)
Normalmente llamamos \(f^{-1}\) a la inversa de \(f\), por lo que la fórmula que define la inversa normalmente se escribe como:
\[ f(f^{-1}(x)) = x \]¿cuáles son los pasos para encontrar la función inversa?
- Paso 1: Comienza con la ecuación que define la función, es decir, comienzas con y = f(x)
- Paso 2: Luego usas manipulación algebraica para resolver x. Dependiendo de qué tan complejo sea f(x), puede resultarle más fácil o más difícil resolver x.
- Paso 3: En algunas circunstancias, simplemente no podrás resolver x, para funciones complejas no lineales f(x)
- Etapa 4: Si puedes resolver x, entonces deberías poder escribir x = g(y)
- Paso 5: Es necesario evaluar si la solución encontrada es única. Es decir, podría resolver x de forma única. En otras palabras, ¿encontraste solo una solución al resolver x? En caso afirmativo, entonces tienes una función inversa; de lo contrario, no hay función inversa
- Paso 6: Si encontraste la inversa resolviendo x = g(y), simplemente cambias el nombre de la variable y escribes f -1 (x) = g(x), lo que hace énfasis en que g(x) ES el inverso real
Si tuviera que usar Cálculo y derivados (pero tenga en cuenta que NO necesita Derivados para calcular la inversa), puede encontrar la derivada de la función y asegurarse de que la derivada sea siempre positiva o negativa, para garantizar que la función sea inyectiva y, por lo tanto, invertible.
Pero normalmente, la metodología de Resolviendo para x es mucho más aceptable para los estudiantes de álgebra básica.
La regla para encontrar funciones inversas
En realidad, no existen otras reglas para calcular la función inversa aparte de comenzar con y = f(x) y luego resolver para x. Una regla como esa suena bastante amplia, porque lo es. Más que una regla, es una metodología genérica para iniciarse en el proceso.
En última instancia, calcular la inversa dependerá de su éxito al resolver una ecuación y de asegurarse de que la solución sea única. Ayuda evaluar la gráfica de la función de antemano, para no buscar una inversa cuando claramente no la hay.
¿Qué mirar en un gráfico? Una función debe ser monótona (creciente o decreciente) en un determinado subdominio para ser invertible. Dicho esto, podríamos restringir convenientemente el dominio de una función a un subdominio más pequeño para encontrar la inversa en un conjunto más pequeño, eso siempre es una posibilidad.

¿cómo sabemos con seguridad que la función tiene inversa?
Formalmente, la única forma de asegurarse de que una función tenga una inversa es asegurarse de que la función sea inyectiva (1 a 1). Esto se evalúa calculando su derivada (si existe) y asegurándose de que sea positiva y negativa en todas partes, o asegurándose manualmente de que cuando comenzamos con y = f(x) y resolvemos para x, siempre obtenemos una única solución.
Esto también se puede ver gráficamente, usando la prueba de la línea horizontal: se dibuja una línea horizontal arbitraria y la función f(x) pasa la prueba de la línea horizontal si alguna línea horizontal dibujada cruza la gráfica de la función como máximo una vez.

Ejemplo: encontrar la función inversa
Encuentra la inversa de la siguiente función: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Solución:
Tenemos la siguiente función:
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Luego, para encontrar la inversa de la función dada, necesitamos resolver \(x\) y determinar si hay una solución o no. La ecuación inicial es:
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Paso 0: En este caso, primero necesitamos simplificar la ecuación lineal dada y, para hacerlo, llevamos a cabo los siguientes pasos de simplificación:
Resolver la ecuación lineal
Poniendo \(x\) en el lado izquierdo y \(y\) y la constante en el lado derecho obtenemos
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Ahora, resolviendo \(x\), al dividir ambos lados de la ecuación entre \(-\frac{1}{3}\), se obtiene lo siguiente
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]y simplificando obtenemos finalmente lo siguiente
\[\displaystyle x=3y-\frac{15}{4}\]Por lo tanto, resolver \(y\) para una ecuación lineal dada conduce a \(x=3y-\frac{15}{4}\).
Por tanto, y como al resolver para \(x\) encontramos solución y es sólo una solución, hemos encontrado la inversa.
La función inversa
Con base en el trabajo mostrado arriba, se puede concluir que la función inversa es:
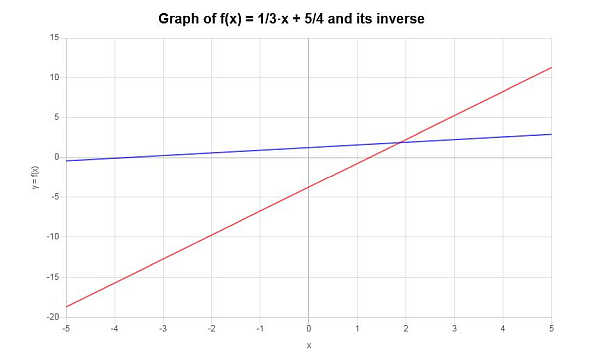
\[f^{-1}(x) = 3x-\frac{15}{4}\]La función inversa se puede representar gráficamente de la siguiente manera:
Ejemplo: más ejemplos inversos
Calcula la función inversa de: \(y = \frac{x-1}{x+3}\)
Solución:
Para encontrar la inversa de la función dada, despejamos \(x\) y determinamos si hay solución o no. La ecuación inicial es:
\[y=\frac{x-1}{x+3}\]Se obtiene lo siguiente:
Ecuación del numerador auxiliar
Necesitamos igualar el numerador a cero y encontrar las soluciones. Entonces, aquellas raíces que no hagan que el denominador sea igual a cero serán soluciones a la ecuación racional
Usando manipulación algebraica de la ecuación polinómica anterior, se obtiene lo siguiente:
\[x = -\frac{3y+1}{y-1} \]Ecuación del denominador auxiliar
Encontramos las raíces del denominador: \(x+3=0\)
Por lo tanto, resolver \(x\) para una ecuación lineal dada conduce a \(x=-3\).
Reuniendo las soluciones de la ecuación racional
Luego, comprobando que no tenemos un cero en el denominador, encontramos la siguiente solución establecida en la ecuación \(\displaystyle y=\frac{x-1}{x+3}\) es
\[x = -\frac{3y+1}{y-1} \]Dado que cuando resolvemos para \(x\) encontramos una y sólo una solución, concluimos que tenemos una función inversa.
Encontrar la función inversa
Con base en el trabajo mostrado arriba, se puede concluir que la función inversa es:
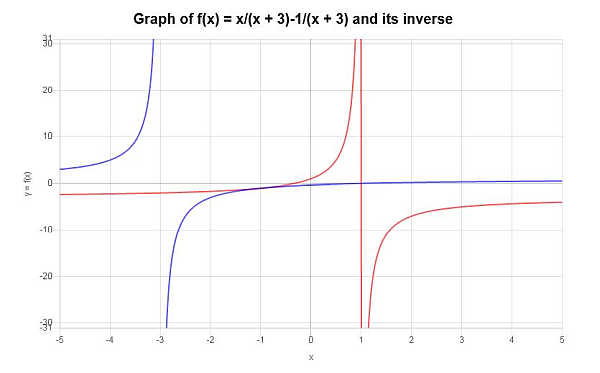
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]La función inversa encontrada se puede representar gráficamente de la siguiente manera:
Ejemplo: no todas las funciones tienen inversa
¿La siguiente función tiene inversa: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \)?
Solución: Observa eso
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]lo que indica que hay dos soluciones, y entonces, no hay inversa en este caso.
Más calculadoras de funciones
Las funciones son un objeto crucial en matemáticas, especialmente en cálculo y álgebra, donde muchas asociaciones entre variables se establecen mediante funciones.
Hay muchas cosas que puedes hacer con la función: puedes simplificarlos , puedes diferenciar una función , puede operarlos, encontrar el compuesto con otra función y la lista continúa.
Muchas veces, incluso si menciona funciones explícitamente, tiene funciones subyacentes a todo el proceso. Así que están ahí, aunque a veces no lo sepas. Una gran cosa es que incluso con los más complicados, siempre puedes graficar una función para tener una idea de su comportamiento, para al menos tener una idea de lo que hace la función (sube, baja, etc.).




