Gráfico de función
Instrucciones: Use esta calculadora de gráficos de funciones para generar el gráfico de una función que proporcione. Escriba cualquier función válida que desee graficar en el cuadro de formulario a continuación.
Gráfico de función
Esta calculadora de gráficos de funciones le permitirá generar el gráfico de cualquier función que proporcione. Debe proporcionar una función válida en x.
Podría ser una función que ya está simplificada, como f(x) = sin(2x), o podría ser algo más complejo como 'f(x) = sin((1/3 x +1/4 x^2) (1/5 x +1/6))', y esta calculadora hará el simplificación de funciones para usted.
Una vez que haya ingresado una función válida en el formulario correspondiente, solo necesita hacer clic en 'Calcular' para generar el gráfico.
Trabajando con el gráfica de una función puede ayudarte a entender sus principales propiedades. En efecto, tener la gráfico de función puede decirte en última instancia todo lo que necesitas sobre el comportamiento de la función: ¿es creciente? ¿Está disminuyendo? ¿cruza el eje x? ¿Tiene algún tipo de simetría?
¿qué es la función gráfica?
El gráfico de función para una función dada f(x) es el conjunto de puntos (x, f(x)). Esto, cuando se dibuja en los ejes x-y, parece una 'curva' (podría ser una línea) que fluye de izquierda a derecha.
Ahora bien, este flujo de izquierda a derecha tiene una propiedad muy específica: pasa la prueba de la línea vertical, que indica que la gráfica de una función, cuando se cruza con cualquier línea vertical, tendrá como máximo un punto de intersección. Por ejemplo, el siguiente gráfico corresponde a un gráfico de función porque pasa la prueba de la línea vertical.
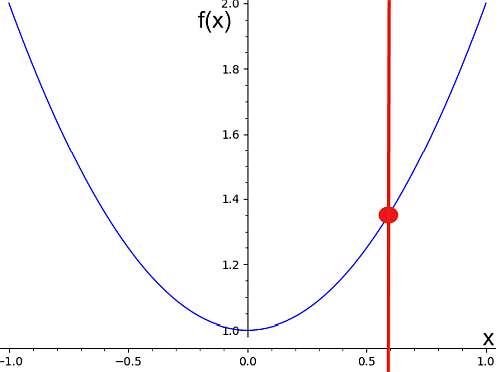
Por otro lado, la gráfica de abajo no corresponde a la gráfica de una función, porque podemos ver una línea vertical que cruza la curva en dos puntos.
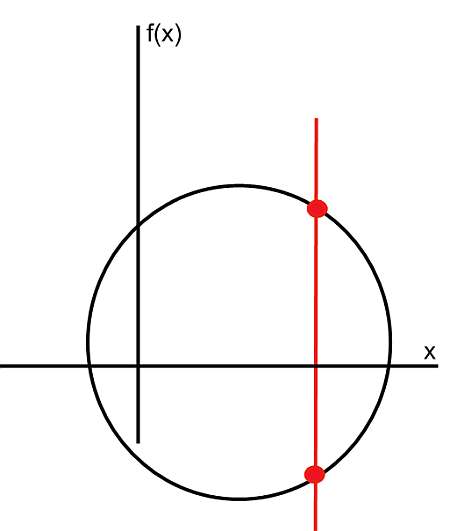
¿cuáles son los pasos para encontrar la gráfica de la función?
- Paso 1: Identifique la función que desea graficar. Por inspección, evaluar si la función es válida o no.
- Paso 2: si la función es una expresión válida, encuentre puntos potenciales donde la función no se pueda evaluar (divisiones por cero o raíces cuadradas de números negativos)
- Paso 3: simplifica tanto como puedas, para poner la función en su forma más simple
- Paso 4: Trate de identificar patrones conocidos. ¿Es la función en su forma más simple un polinomio? Los polinomios tienen una forma específica. ¿La función es una función trigonométrica? También tienen una forma muy conocida y característica.
- Paso 5: Si no tiene ningún patrón simple y reconocible o función conocida, cree una tabla de puntos (x, f(x)), tantos puntos como sea práctico
- Paso 6: Traza esos puntos de tu tabla en el plano XY. Trace una curva a través de esos puntos para tener una idea de cómo se ve el gráfico de la función
Simplificando la función a su forma más simple le ayudará a identificar de una manera más fácil cualquier función conocida que aparezca y pueda graficarse fácilmente.
¿cómo graficar funciones conocidas?
Cuándo simplificando una función , no espere tener directamente cosas muy simples como \(f(x) = x^2\) (una parábola simple) o \(f(x) = x\) (una línea simple), pero puede tener traducciones de versiones escaladas de esas básicas. En efecto, por ejemplo, cualquier función cuadrática se puede poner en Forma de vértice , que te ayuda a identificar la curva como una parábola simple que se traslada.
¿cuáles son los pasos para hacer transformaciones de gráficos de funciones?
- Paso 1: Identifique la función que desea graficar
- Paso 2: simplifica tanto como puedas evitando la trampa de dividiendo por cero y sacando la raíz cuadrada de los valores negativos
- Paso 3: con la versión más simple de la función, vea si se pueden reconocer funciones elementales
- Paso 4: Si no, vea si alguna transformación de funciones comunes (polinomios, rectas, funciones trigonométricas , etc.) se pueden identificar, ya que también son fáciles de graficar
- Paso 5: si todo lo anterior falla, simplemente construya una tabla con valores (x, f(x)) y trace manualmente la forma del gráfico
Por supuesto, no tiene que graficarlo manualmente, puede usar este gráfico de funciones herramienta para obtener un gráfico preciso y ordenado.
¿por qué le gustaría saber acerca de los tipos de gráficos de funciones?
El gráfico de una función esencialmente puede decirte todo sobre la función. Hasta cierto punto, la gráfica de la función ES la función , o al menos una representación de ella.
Existe una correspondencia entre la función y el gráfico, lo que indica que el gráfico esencialmente te dice todo lo que necesitas saber sobre la función.
Ejemplo: encontrar el gráfico de la función
Calcula la función gráfica de lo siguiente: \(f(x) = \frac{1}{4}(x-3)^2 + \frac{5}{4} x - \frac{5}{6}\)
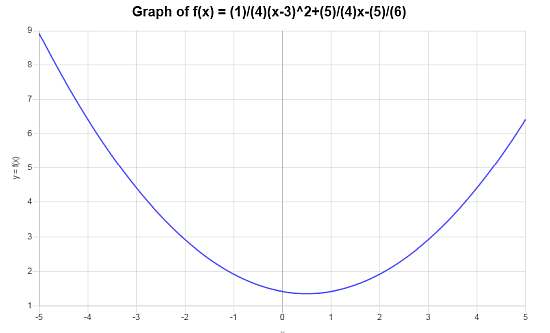
Solución: Se ha proporcionado la siguiente función \(\displaystyle f(x) = \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6}\) para la cual necesitamos construir su gráfico.
Paso 0: En este caso, primero necesitamos simplificar la función dada \(\displaystyle f(x) = \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6} \), y para hacerlo, llevamos a cabo los siguientes pasos de simplificación:
Se obtiene el siguiente gráfico para la función simplificada \(\displaystyle f(x)=\frac{1}{4}x^2-\frac{1}{4}x+\frac{17}{12}\) en el intervalo \([-5, 5]\):
Ejemplo: reglas de gráficos de funciones
Calcula la gráfica de la función \(f(x) = \frac{1}{3}(x-4)^2 - \frac{5}{6}\). ¿Es esta función una transformación gráfica de función de una función básica bien conocida?
Solución: Expandiendo y simplificando la función:
Se obtiene el siguiente gráfico para \(\displaystyle f(x)=\frac{1}{3}x^2-\frac{8}{3}x+\frac{9}{2}\) en el intervalo \([-10, 10]\):
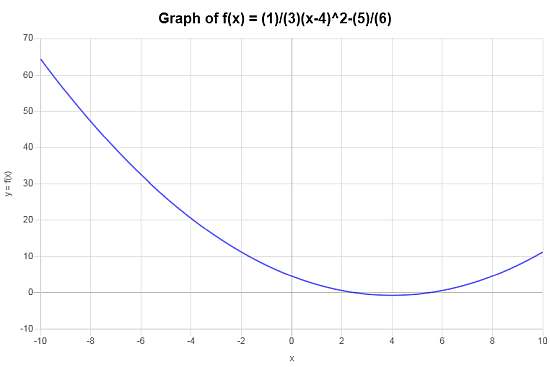
En este caso, el gráfico es \(f(x) = \frac{1}{3}(x-4)^2 - \frac{5}{6}\), de hecho, la transformación del simple \(g(x) = x^2\), que se ha desplazado 4 unidades hacia la izquierda, desplazado hacia abajo en \(\frac{5}{6}\) y reescalado.
Ejemplo: otro ejemplo de gráfico de función
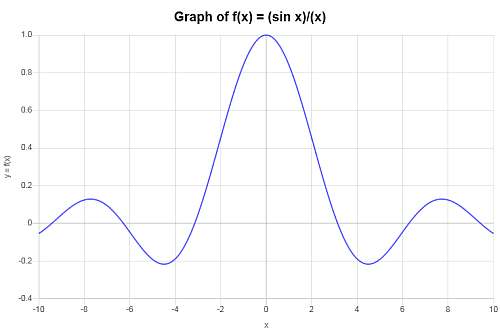
Calcula la gráfica de \( f(x) = \displaystyle \frac{\sin(x)}{x}\).
Solución: Se ha proporcionado la siguiente función: \(\displaystyle f(x) = \frac{\sin\left(x\right)}{x}\), por lo que se obtiene el siguiente gráfico, intervalo \([-10, 10]\):
Otras calculadoras de funciones
Dada una función, querrá poder simplificar la función , para decirlo en su forma más simple. Ya vimos que es beneficioso identificar de una manera más fácil la transformación potencial del gráfico de funciones a partir de funciones básicas que pueden estar allí.





