El dominio de una función es un conjunto donde una función está bien definida. Más específicamente, deje que \(f: D \rightarrow R\) sea una función, lo que significa que \(f(a)\) está bien definido para \(a \in D\). El dominio de la función \(f\) es el conjunto \(D\).

Matemáticamente escribirás \(dom(f) = D\).

El rango de una función, por otro lado, es un conjunto de valores que se pueden alcanzar a través de la función.

Más específicamente, sea \(f: D \rightarrow R\) una función, el rango es el conjunto de todos los valores posibles \(b \in R\) para los que existe \(a \in D\) tales que \(f(a) = b\).

A menudo, el rango de una función se escribe como \(R(f)\) o también como \(f(D)\) (que también se conoce como el conjunto de imágenes de \(D\) mediante la función \(f\)).

Es crucial conocer el dominio de una función porque eso nos da un conjunto seguro de valores en los que la función está bien definida.

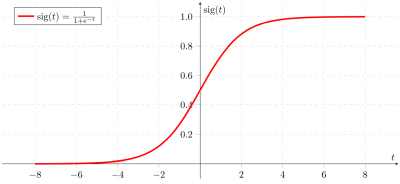
Entonces, el rango es importante porque nos dice qué valores alcanza la función. Una interpretación más gráfica es la siguiente: Un punto \(b\) está en el rango de \(f\) si la línea horizontal \(y = b\) interseca la gráfica de la función \(f(x)\).

¿Cómo calcular el dominio, en términos prácticos?

A continuación se explica cómo encontrar el dominio y el rango. :

Para el dominio, primero debe encontrar los puntos donde la función NO está definida. Las fuentes de las operaciones indefinidas son la división por cero o la raíz al cuadrado de números negativos.

Entonces, necesita encontrar esos puntos (si los hay) donde ocurren esas operaciones indefinidas. Y el dominio será el resto de los puntos, es decir, todos los puntos excluyendo aquellos que encuentres que causan operaciones indefinidas.

¿Cómo calcular el rango, en términos prácticos?

Sea \(y\) un número y resolveremos para \(x\) la siguiente ecuación \(f(x) = y\). El valor \(y\) está en el rango si \(f(x) = y\) se puede resolver para \(x\).

Entonces, esto es un poco más complicado: debe averiguar si necesita restringir \(y\) de alguna manera para que \(f(x) = y\) tenga una solución para \(x\).

EJEMPLO 1

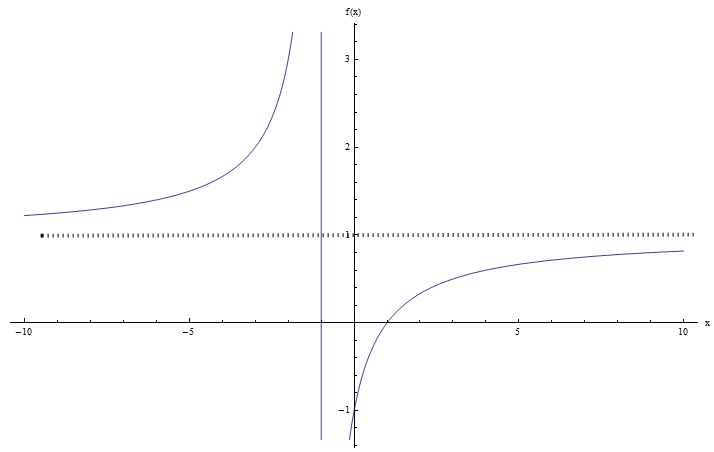
Calcule el dominio y rango de la función \(\displaystyle f(x) = \frac{x+1}{x-1}\).

RESPONDEDOR:

Primero, necesitamos calcular el dominio. Necesitamos ver dónde está bien definida la función. Por lo general, es más fácil comenzar donde NO está bien definido.

Entonces, en este caso, todas parecen ser operaciones válidas, excepto por una cosa: el denominador no puede ser cero.

No un: Las principales claves para encontrar el dominio es identificar los puntos donde hay posibles divisiones por cero, o posibles raíces cuadradas de valores negativos, que son operaciones inválidas.

Por lo tanto, la función está bien definida EXCEPTO cuando \(x-1 = 0\), que ocurre cuando \(x = 1\). Por lo tanto, decimos que el dominio es la línea real completa excepto por el valor \(1\).

Usando la notación de intervalo, escribiríamos \(dom(f) = (-\infty, 1) \cup (1, +\infty)\).

Ahora necesitamos calcular el rango. Por lo general, puede ser un poco más laborioso obtener el rango que obtener el dominio, pero aquí vamos.

Hay muchas formas de encontrar el rango: algunas pueden depender de la representación gráfica de la función para hacer una afirmación sobre el rango de una función. Eso podría funcionar, pero no es una respuesta real, solo una corazonada educada.

La otra forma es la forma matemática formal: Sea \(y\) un número y resolveremos para \(x\) la siguiente ecuación \(f(x) = y\). El valor \(y\) está en el rango si \(f(x) = y\) se puede resolver para \(x\).

En este caso tenemos:

Entonces, ¿cuándo está \(x\) bien definido? Casi para todos \(y\), excepto cuando \(y = 1\), porque en ese caso tenemos una división por \(0\). Por lo tanto, el rango de \(f\) en este caso es la línea real completa, excepto 1.

Usando la notación de intervalo, escribiríamos \(R(f) = (-\infty, 1) \cup (1, +\infty)\).

EJEMPLO 2

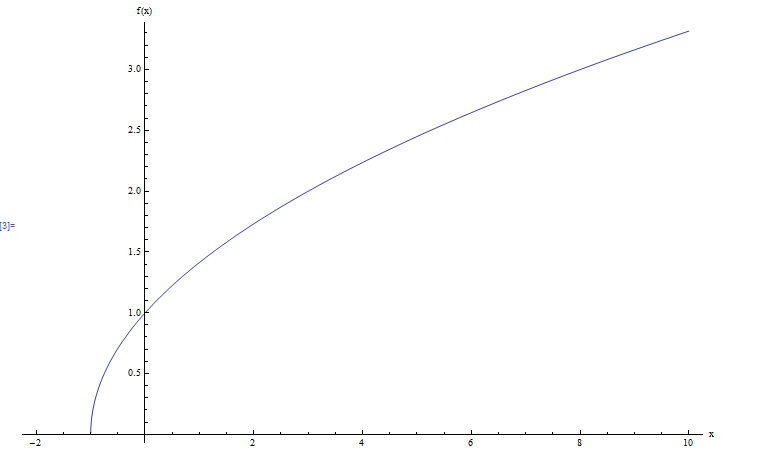
Calcule el dominio y rango de la función \(\displaystyle f(x) = \sqrt{x+1}\).

RESPONDEDOR:

Recuerde, para encontrar el dominio necesitamos buscar puntos donde puedan ocurrir operaciones no válidas (divisiones por cero o raíces cuadradas de valores negativos. No hay divisiones en este caso, pero debemos asegurarnos de que \(x+1\ge 0\) para que no haya raíces cuadradas de valores negativos necesitamos. \(x \ge -1\). Usando notación de intervalo, escribiríamos \(dom(f) = [-1, +\infty)\).

Ahora, para el rango, necesitamos resolver \(x\): \(\sqrt{x+1} = y\). La raíz cuadrada de algo nunca es negativa, así que al menos necesitamos ese \(y \ge 0\).

Además, al aplicar cuadrado a ambos lados, obtenemos \(x+1 = y^2\), por lo que la solución es \(x = y^2-1\). Entonces, la única restricción que debemos imponer a \(y\) es que \(y \ge 0\). Por lo tanto, usando la notación de intervalo, escribiríamos \(R(f) = [0, +\infty)\). Gráficamente: