Más sobre ecuaciones lineales

Esta calculadora lo ayudará a graficar una ecuación lineal que proporcione. Entonces, el primer paso es proporcionar una ecuación lineal válida, algo así como 2x + 3y = 4, o también podría proporcionar algo que no venga directamente simplificado, como 2/3 x + y = 4/3 x - 1/ 2 y + 2. Cualquier expresión lineal válida funcionará. .

Una vez que proporciona una ecuación lineal válida, llega la parte fácil, ya que todo lo que necesita hacer es hacer clic en "Calcular", y se le mostrarán los pasos del proceso de graficar la función lineal.

Las ecuaciones lineales jugarán un papel importante en muchas operaciones, incluso para resolver un sistema de ecuaciones lineales .

Fórmula de ecuación lineal

Hay diferentes formas en las que puedes escribir una fórmula de ecuación lineal. Los más comunes son los formulario estándar , que se muestra a continuación

\[a x + by = c \]

También, está el forma de intersección de pendientes , que se muestra a continuación

\[y = mx + n\]

La mayoría de estas dos formas se pueden convertir de una a otra, excepto por un par de excepciones, a saber, la línea vertical expresada por x = a. Esta línea es vertical y cruza el eje x en (a, 0). Tenemos que x = a es la forma estándar de la recta, pero esta recta no tiene pendiente-intersección (al menos donde y es la variable dependiente)

¿cuáles son los pasos para graficar una ecuación lineal?

• Paso 1: Identifique claramente la ecuación disponible
• Paso 2: Mira el coeficiente que multiplica y, si es cero, entonces tienes una línea vertical
• Paso 3: Si el coeficiente que multiplica y es diferente de cero, entonces resuelves para y para obtener el forma de intersección de pendientes
• Paso 4: usando la forma pendiente-intersección, evalúa la función en x = 0 y x = 1, y luego tienes dos puntos por donde pasa la línea
• Paso 5: Dibuja una línea usando esos dos puntos que encontraste como guía

Una de las formas más claras de dibujar una línea es tener dos puntos por donde pasa la línea, ya que muchas veces usar la pendiente para guiarse puede ser engañoso.

Solución de ecuación lineal en una variable

Los estudiantes están familiarizados con los sistemas de ecuaciones lineales y entienden más o menos lo que hay que hacer. Pero luego se preguntan sobre la solución de una ecuación lineal en una variable. Digamos que tienes la ecuación lineal en forma de pendiente-intersección:

\[y = a + bx \]

Entonces, ¿cómo resuelves eso? Bueno, ya está resuelto: para cada valor dado de x, la solución de y es y = a + bx. Entonces, siempre que \(b \ne 0\), tenga infinitas soluciones para una ecuación lineal.

La situación cambia cuando tienes dos ecuaciones lineales, en cuyo caso necesitas resolver ambas ecuaciones simultáneamente .

¿son las ecuaciones lineales tan importantes?

¡Apuesta! Quizás entre los más importantes de todo el Math. Esto se debe a la simplicidad y, sin embargo, a la amplia gama de aplicaciones.

Ejemplo: calculadora de ecuación lineal

Obtén la gráfica de la siguiente ecuación lineal: \(\frac{1}{3} x + \frac{7}{4} y - \frac{5}{6} = 0\)

Solución:

Obtenga la ecuación de la línea en forma de pendiente-intersección

Se nos ha dado la siguiente ecuación:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Simplificando las constantes:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Ahora, poniendo \(y\) en el lado izquierdo y \(x\) y la constante en el lado derecho obtenemos

\[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Ahora, resolviendo para \(y\), dividiendo ambos lados de la ecuación por \(\frac{7}{4}\), se obtiene lo siguiente

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\]

y simplificando obtenemos finalmente lo siguiente

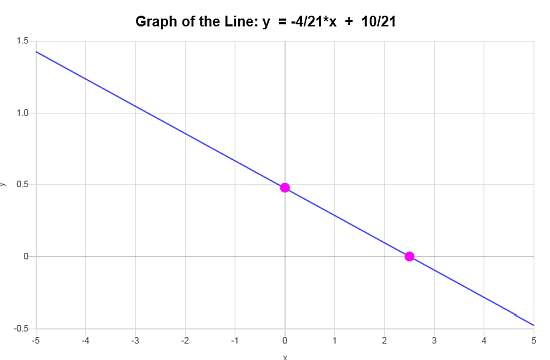
\[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\]

Conclusión : Inferimos que la ecuación de la línea en forma de pendiente-intersección basada en los datos disponibles es: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), con una pendiente de \(\displaystyle b = -\frac{4}{21}\) y una intersección en y de \(\displaystyle n = \frac{10}{21}\).

Teniendo en cuenta estos datos, el gráfico de líneas proporcionado muestra

Ejemplo: ejemplo de calculadora de ecuación lineal

Calcula lo siguiente: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\)

Solución: Ahora se nos ha proporcionado la siguiente ecuación:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

El primer paso es simplificar las constantes:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Poniendo \(y\) en el lado izquierdo y \(x\) y el término constante en el lado derecho, obtenemos

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\]

Ahora, necesitamos resolver para \(y\), y eso se logra dividiendo ambos lados de la ecuación por \(\frac{5}{4}\), y se obtiene lo siguiente

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\]

y simplificando obtenemos finalmente lo siguiente

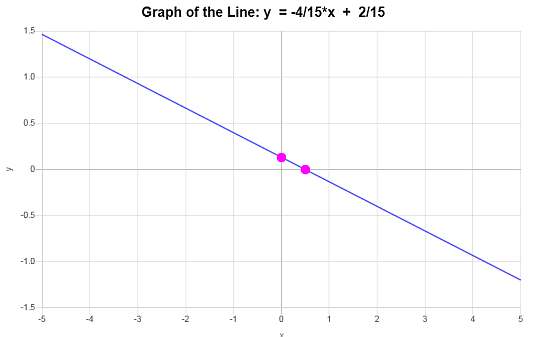
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\]

Conclusión : La ecuación de la línea en forma de pendiente-intersección es, de acuerdo con la información proporcionada, \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), con una pendiente de \(\displaystyle b = -\frac{4}{15}\) y una intersección en y de \(\displaystyle n = \frac{2}{15}\).

De acuerdo con estos datos, el gráfico lineal presentado es

Ejemplo: otro ejemplo de calculadora de ecuación lineal

¿Esto representa una línea: \( y = 5 \). Si es así, ¿cuáles son sus características?

Solución: Sí lo hace. De hecho, cuando tienes una expresión como \( y = 5 \), tienes una ecuación lineal en forma de pendiente-intersección, con a = 0 y b = 5. Por lo tanto, lo que tenemos es una línea que es horizontal, que cruza la y -eje en el punto (0, 5).

Más calculadoras de álgebra

Líneas , Ecuaciones lineales y funciones lineales siempre jugará un papel crucial en Álgebra, presentando también un vínculo claro con algunas propiedades geométricas básicas.

En términos de aplicaciones, quizás resolver sistemas de ecuaciones lineales es una de las aplicaciones más comunes de rectas y ecuaciones lineales.