Löser Infinitesimalrechnung

Inverse trig -derivate

Anweisungen: Verwenden Sie diesen Taschenrechner, um Ableitungen von inversen Triggfunktionen zu finden und alle Schritte anzuzeigen.Bitte geben Sie die Funktion ein, die eine inverse Trig -Funktion im folgenden Formularfeld enthält.

Inverse trig -derivate

Mit diesem Taschenrechner können Sie Derivate von inversen Triggfunktionen berechnen und alle Schritte des Prozesses anzeigen.

Die Idee ist, dass die von Ihnen bereitgestellte Funktion eine inverse Trig -Funktion enthält, zum Beispiel f (x) = x^2/arctan (x+1), nur um ein Beispiel zu geben.

Wenn Sie bereit sind und fertig sind und die Funktion, die Sie zur Unterscheidung benötigen, eingeben, klicken Sie auf die Schaltfläche "Berechnen", um alle Schritte des Prozesses und der Berechnungen anzuzeigen.

Die Idee von Berechnung von Derivaten von inversen Trig -Funktionen ist natürlich, und wir werden in den nächsten Absätzen sehen, dass sie direkt von der abgeleitet werden können Trig -Dederivat dass Sie wissen.

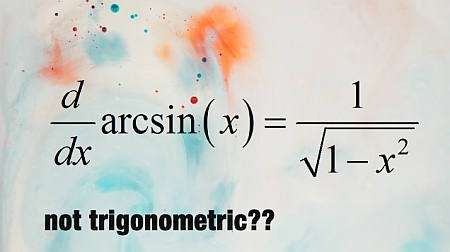
Inverse triggfunktionen

In einfachen Worten ist die inverse Trig -Funktion die Funktion, die bei der Bewertung an der entsprechenden Trig -Funktion zur Identität führen.Wenn wir beispielsweise die Funktion betrachten \(\sin(x)\), ist die inverse Funktion \(\arcsin(x)\) und diese Inverse hat die Eigenschaft

\[\sin(\arcsin(x)) = x \]

ebenso gut wie

\[\arcsin(\sin(x)) = x \]

für alle \(x\) in einem bestimmten Intervall.Also streng, \(\arcsin(x)\) ist die inverse Funktion von \(\sin(x)\) aus algebraischer Sicht.Das Gleiche gilt für die anderen inversen Triggfunktionen und ihre entsprechenden Triggfunktionen.

Inverse trig -derivateberechnung

Also, wenn \(f\) eine Funktion ist und eine inverse \(f^{-1}\) hat, dann haben wir das

\[f^{-1}(f(x)) = x\]

für alle \(x\).Wenn wir dann beide Seiten der Gleichheit unterscheiden und die Kettenregel auf der linken Seite verwenden, bekommen wir

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

Wenn wir nun \(y = f(x)\) festlegen, dann \(x = f^{-1}(y)\), was zu

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

Wie verwenden wir dies für inverse Trig -Funktionen?Angenommen \(f(x) = \sin(x)\) und \(f^{-1}(x) = \arcsin(x)\).Dann bekommen wir gemäß der allgemeinen Beziehung zwischen der Ableitung einer Funktion und der Ableitung ihrer Umkehrung

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

Aber ein ordentlicher geometrischer Trick erzählt uns das

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

das impliziert das

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

Der Rest von inversen Trig -Derivaten wird mit ähnlichem Argument erhalten.

Was sind die 6 grundlegenden inversen trig -funktionen?

#1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
#2: \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
#3: \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
#4: \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
#5: \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
#6: \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

Interessanterweise beinhaltet keiner der inversen Trig -Derivate bei der Berechnung des Derivats von inversen Trig -Funktionen entweder Triggfunktionen oder inverse Triggfunktionen.

Anwendungen des derivats inverser trigonometrischer funktionen

Trigendefunktionen und ihre Derivate sowie inverse Trig -Funktionen und ihre Derivate sind Teil des Inventars der grundlegenden Funktionen und Operationen, die als Bausteine verwendet werden, um kompliziertere Funktionen zu erstellen.

Obwohl Triggfunktionen in Anwendungen häufiger als inverse Trig -Funktionen auftreten, haben letztere auch einen klaren Ort im Kalkül, insbesondere bei der Differenzierung und Verwendung der Partialdosenzersetzungsmethode.

Tipps und tricks

Vergessen Sie nicht, dass die Derivate von inversen Triggfunktionen äußerst nützlich sein können, insbesondere bei der Integration von Begriffen mit einem quadratischen Nenner.

Außerdem ist es einfach, Fehler bei der Berechnung von inversen Trig -Derivaten per Definition zu machen. Sie könnten definitiv von der Verwendung von a profitieren Derivatnetisch Dadurch werden die Schritte angezeigt oder mit der Sie Ihre Arbeit überprüfen können.

Beispiel: inverse trig -derivate

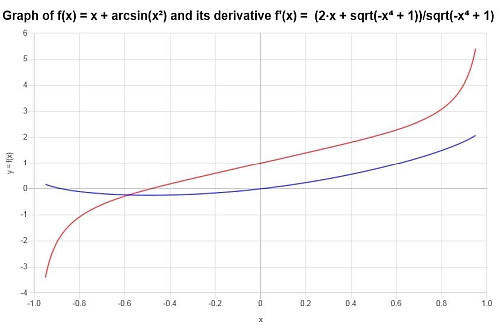
Berechnen Sie die Ableitung von: \(f(x) = x + \arcsin(x^2)\)

Lösung: Für dieses erste Beispiel werden wir \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\) analysieren.Diese Funktion beinhaltet eine inverse Trig -Funktion, die mit einer anderen Funktion verstärkt wird.Berechnen wir sein Derivat:

\( \displaystyle \frac{d}{dx}\left(x+\arcsin\left(x^2\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x+\arcsin(x^2) \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin(x^2)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

But we know already that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)\)

By using the Chain Rule: \(\frac{d}{dx}\left( \arcsin\left(x^2\right) \right) = \frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-\left(x^2\right)^2}}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle 1+\frac{2x}{\sqrt{1-x^4}}\)

Antworten : Wir können zu dem Schluss kommen, dass die Ableitung der Funktion lautet:

\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

Wir können sowohl die Funktion als auch ihre Ableitung in der folgenden Grafik sehen:

Beispiel: mehr umgekehrte trig -derivate

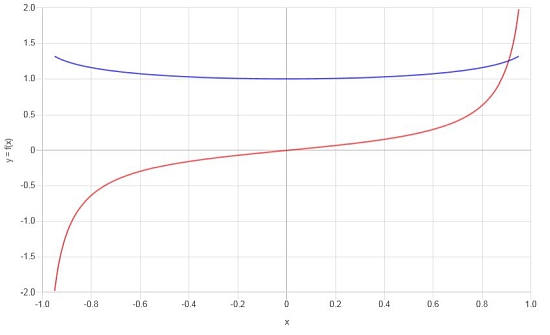
Betrachten Sie die folgende Funktion: \(f(x) = \frac{\arcsin(x)}{x}\), berechnen Sie das Abgang.

Lösung: Nun zum zweiten Beispiel haben wir die Funktion \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\).

\( \displaystyle \frac{d}{dx}\left(\frac{\arcsin\left(x\right)}{x}\right)\)

The Quotient Rule applies in this case: \(\frac{d}{dx}\left( \frac{\arcsin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \arcsin\left(x\right) \right) = \frac{1}{\sqrt{1-\left(x\right)^2}}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{1}{\sqrt{1-\left(x\right)^2}}-\arcsin\left(x\right)}{x^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\frac{1}{\sqrt{1-x^2}}x-\arcsin\left(x\right)}{x^2}\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(\sqrt{1-x^2}\cdot \arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\)

Schlußfolgerung : Die Ableitung, nach der wir suchen, ist:

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

Grafisch haben wir Folgendes:

Inverse trig -derivate beispiel

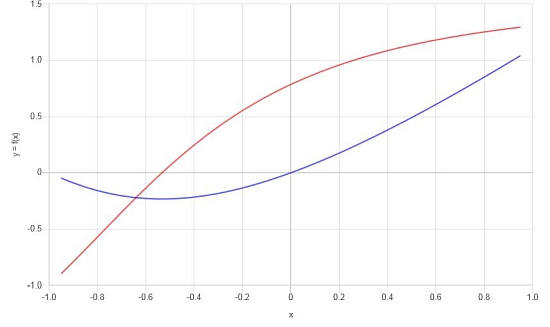
Berechnen Sie die Ableitung von: \(f(x) = x \arctan(x+1)\)

Lösung: Für dieses letzte Beispiel werden wir mit der Funktion \(\displaystyle f(x)=x\arctan\left(x+1\right)\) arbeiten, die eine umgekehrte Funktion enthält.

\( \displaystyle \frac{d}{dx}\left(x\arctan\left(x+1\right)\right)\)

The Product Rule applies in this case: \(\frac{d}{dx}\left( x\arctan\left(x+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \arctan\left(x+1\right) \right) = \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)}{1+\left(x+1\right)^2}\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)}{1+\left(x+1\right)^2}\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{1}{1+\left(x+1\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)^2}+\arctan\left(x+1\right)\)

We expand the terms: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Reducing the one in \(x\cdot 1 = x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)\)

Finally, the following is obtained

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\)

Fazit : Nach der Vereinfachung ist das Derivat::

\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

Basierend auf den gefundenen Ergebnissen können wir das folgende Diagramm für F und F 'erstellen:

Andere kalkülrechner

Beim Benutzen Trig -Dederivat Wir gaben an, dass sie entscheidende Bausteine für die Anwendung von Basic waren Fähigkeitsregeln .

Derivate für inverse Triggfunktionen können einfach von der abgeleitet werden Derivat von grundlegenden Trig -Derivaten, und deshalb betrachten wir sie auch innerhalb der Gruppe grundlegender Derivate, um zu lernen oder sogar auswendig zu lernen.