Solveurs Algèbre

Graphique polynomial

Instructions: Utilisez cette calculatrice pour tracer des graphiques de fonctions polynomiales, pour créer le graphique de n'importe quelle fonction polynomiale que vous fournissez dans le formulaire ci-dessous :

Graphique polynomial

Utilisez cette calculatrice si vous avez besoin d'aide pour représenter graphiquement une fonction polynomiale. Le processus est simple : il vous suffit de taper la fonction polynomiale que vous voulez représenter. Vous pouvez écrire quelque chose comme '3x^3 + x - 1', ou vous pouvez le faire précéder du nom de la fonction, comme 'p(x) = 3x^3 + x - 1'.

Les coefficients du polynôme fourni ne doivent pas nécessairement être des entiers, ils peuvent être des fractions ou toute expression algébrique valide. Le polynôme que vous fournissez peut être simplifié ou non, cela n'a pas d'importance.

Ensuite, une fois que le polynôme a été fourni, vous pouvez éventuellement déterminer les plages de valeurs de x qui seront représentées graphiquement, puis vous cliquez sur "Calculer", et sous peu, toutes les étapes du processus seront affichées.

fonctions polynomiales sont l'un des objets les plus importants que vous trouverez en algèbre ainsi qu'en calcul. En outre, les polynômes entraînent la nécessité de résoudre des équations polynomiales, qui ont de nombreuses applications partout, dans tous les aspects de la vie, même au-delà des mathématiques.

Notions de base sur les fonctions polynomiales

Rappelons qu'une fonction polynomiale a la forme suivante :

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

où nous supposons que $a_n \ne 0$, et nous disons que la degré du polynôme dans ce cas est égal à $n$, et le coefficient principal est $a_n$. La manière profane de définir le degré d'un polynôme est qu'il correspond à la plus grande puissance présente dans l'expression du polynôme.

Par exemple, $p(x) = 3x^2 + 2x - 1$ est un polynôme de degré 2, et son coefficient principal est 3. Maintenant, $p(x) = \sin(3x^2 + 2x - 1)$ n'est PAS un polynôme, par exemple.

Comment faire des graphes de polynômes ?

La représentation graphique des polynômes est en principe identique à celle de toute autre fonction. Si vous deviez le faire à la main, vous tabuleriez plusieurs valeurs pour x et y, et vous traceriez une courbe qui passerait plus ou moins par les points que vous obtenez dans votre tableau.

Naturellement, cette méthode est un peu primitive, car en général, nous ne pouvons pas nécessairement connaître le graphe complet d'une fonction en connaissant simplement un tas de points que nous tabulons.

Heureusement, pour les polynômes, la tâche est un peu plus facile, et en réalité, nous pouvons en savoir beaucoup sur son graphe en connaissant son coefficient principal et son degré.

Étapes de la représentation graphique des fonctions polynomiales

Le graphe d'un polynôme dépend finalement du coefficient spécifique de chaque polynôme. Mais nous pouvons faire quelques déclarations fortes sur le comportement final d'un polynôme et l'existence de racines réelles.

Rappelons que le comportement final d'un polynôme est le comportement du polynôme lorsque x est très grand et négatif, et lorsque x est très grand et positif.

Étape 1: Identifiez la fonction polynomiale et simplifiez-la si vous le pouvez, car il est plus facile de représenter graphiquement des expressions simplifiées
Étape 2: Connaissez-vous les racines du polynôme ? Si ce sont des racines réelles, vous connaissez les points où le polynôme croise l'axe des x, ce qui vous donne une référence graphique forte
Étape 3: Si le degré du polynôme est impair, le comportement final sera opposé pour de grandes valeurs de x négatives et de grandes valeurs de x positives. Si le coefficient principal est positif, pour de grandes valeurs négatives de x, le polynôme sera très grand et négatif, et pour de grandes valeurs positives de x, le polynôme sera très grand et positif. Si le coefficient de tête est négatif, pour de grandes valeurs négatives de x, le polynôme sera très grand et positif, et pour de grandes valeurs positives de x, le polynôme sera très grand et négatif
Étape 4: Si le degré du polynôme est pair, alors le comportement final sera le même pour de grandes valeurs négatives de x et de grandes valeurs positives de x. Si le coefficient principal est positif, pour de grandes valeurs négatives et positives de x, le polynôme sera très grand et positif. Si le coefficient de tête est négatif, pour de grandes valeurs négatives et positives de x, le polynôme sera très grand et négatif
Étape 5 : Si le degré du polynôme est impair, le polynôme croisera au moins une fois l'axe des x (il a donc au moins une racine réelle), alors que pour un degré pair, le polynôme ne croisera pas nécessairement l'axe des x
Étape 6 : Un polynôme de degré n traversera l'axe des x au plus n fois. Par exemple, un polynôme de degré 4 peut traverser l'axe des x au plus 4 fois

Ainsi, par exemple, un polynôme cubique peut traverser l'axe des x au maximum 3 fois, mais il n'est pas obligé de le faire.

Calculatrice graphique

Quels sont les avantages de l'utilisation d'une calculatrice graphique ? Plusieurs. Cela ne veut pas dire qu'il n'est pas bon d'avoir la compétence de pouvoir tracer avec précision un polynôme à l'aide d'un stylo et d'un papier.

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

Avantage 1 : Tu t'assures d'obtenir une représentation précise de la courbe réelle du polynôme
Avantage 2 : Vous pouvez l'utiliser pour vérifier votre propre travail, pour vous assurer que vous avez suivi les bonnes étapes
Avantage 3 : Une bonne calculatrice peut choisir une fenêtre appropriée pour montrer les aspects les plus pertinents du graphique

Un bon graphique peut vous en apprendre beaucoup sur les propriétés d'une fonction, et il en va de même pour un polynôme. La représentation graphique des polynômes peut vous aider à visualiser réellement le type de racines du polynôme.

Conseils et astuces

Faites attention à ne pas trop interpréter ce que vous voyez dans un graphique polynomial. Vous ne pouvez pas dire grand-chose des racines à multiplicité, donc rien ne remplace la fonction réelle.

Si vous voulez essayer d'autres types de fonctions, essayez ceci graphique de la fonction outil.

Représentation Graphique Des Fonctions Polynomiales

Exemple : représentation graphique de fonctions polynomiales

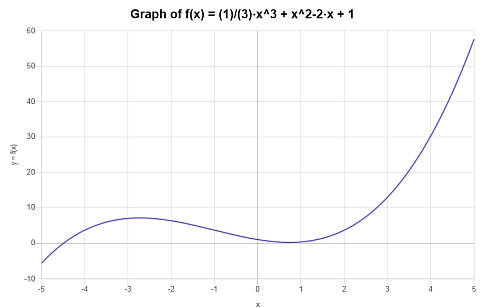
Tracez le graphique du polynôme suivant : $p(x) = \frac{1}{3} x^3 + x^2- 2x +1 $

Solution: On nous fournit l'expression polynomiale suivante que nous devons calculer : $\displaystyle \frac{1}{3} x^3 + x^2- 2x +1$.

L'expression fournie est irréductible, il n'y a donc rien à simplifier.

On obtient le tracé suivant pour l'expression polynomiale donnée sur l'intervalle $[-5, 5]$ :

Exemple : graphique polynomial

Simplifiez et représentez graphiquement : $p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}$

Solution: Maintenant, nous devons travailler avec : $\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}$.

On obtient la simplification suivante :

$ \displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}$

Grouping the terms with $x^3$

$ \displaystyle = \,\,$

$\displaystyle \left(-1-\frac{1}{3}\right)x^3+x^2+2-\frac{3}{2}$

Grouping together numerical values and fractions and simplifying those terms that were grouped with $x^3$

$ \displaystyle = \,\,$

$\displaystyle -\frac{4}{3}x^3+x^2+2-\frac{3}{2}$

Grouping and operating all the integer terms and fractions: $\displaystyle 2-\frac{ 3}{ 2}=2 \times \frac{ 2}{ 2}-\frac{ 3}{ 2}=\frac{ 2 \times 2-3}{ 2}=\frac{ 4-3}{ 2}=\frac{ 1}{ 2}$

$ \displaystyle = \,\,$

$\displaystyle x^2+-\frac{4}{3}x^3+\frac{1}{2}$

By reorganizing/simplifying/expanding the terms that are amenable to

$ \displaystyle = \,\,$

$\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}$

ce qui conclut le processus de simplification polynomiale.

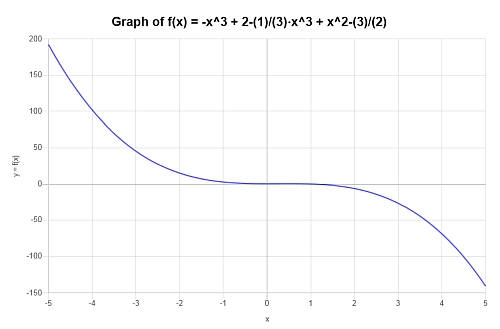
Ainsi donc, on obtient le tracé suivant pour $\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}$ sur l'intervalle $[-5, 5]$ :

Exemple : plus de graphes polynomiaux

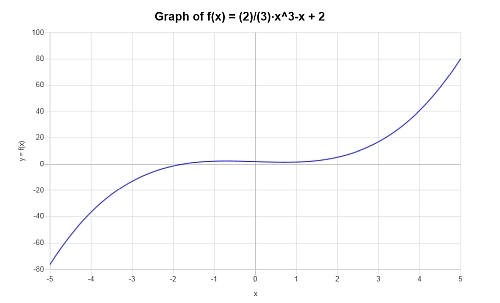
Trouvez le graphique du polynôme suivant $ p(x) = \frac{2}{3} x^3 - x +2 $.

Solution: Pour cet exemple, le polynôme fourni est : $\displaystyle \frac{2}{3} x^3 - x +2 $.

Dans ce cas, l'expression fournie est irréductible, il n'y a donc rien à simplifier.

On obtient le tracé suivant pour l'expression polynomiale donnée sur l'intervalle $[-5, 5]$ :

Plus de calculateurs de polynômes

La représentation graphique des polynômes est extrêmement utile car elle nous montre les principales caractéristiques de leur comportement autour de leurs racines et leur comportement final. La représentation graphique va généralement de pair avec l'identification approximative de l'emplacement des racines, ce qui peut être utile pour factorisation de polynômes également.

Bien que nous puissions en savoir beaucoup sur le polynôme juste en le représentant graphiquement, nous devons toujours passer par le processus d'essayer de trouver des racines rationnelles comme point de départ pour résolution d'équations polynomiales avec un degré supérieur à 2 (ceci, qui ne sont pas équations quadratiques ).

Deviner ou trouver systématiquement des racines rationnelles, tout en utilisant Division longue ou Division synthétique donc d'utiliser le théorème des facteurs peut conduire à une recherche fructueuse de racines polynomiales mais cette approche ne fonctionne pas toujours, et il faut souvent faire appel à la calculatrice pour trouver des approximations numériques.