Le concept de fonction est extrêmement important et il est absolument omniprésent en mathématiques. C'est pourquoi nous devons lui donner un bon coup de pouce, avant d'essayer de comprendre certains des avantages qui viendront par la suite lorsque nous approfondirons les sujets de calcul, tels que la différenciation et l'intégration.

QU'EST-CE QU'UN SET?

Le premier élément que nous devons comprendre est le concept d'un ensemble . Un ensemble est simplement une collection d'éléments. Ainsi donc, un ensemble est tout simplement défini en sachant quels éléments appartiennent à l’ensemble et quel élément n’en fait pas. Cela semble être une tâche extrêmement simple et la théorie de l'ensemble devrait être simplement réduite à avoir des règles sans ambiguïté pour déterminer quels éléments appartiennent à un ensemble.

Par exemple, définissons l'ensemble des nombres pairs, et nous l'appelons \(E\). Pourquoi est-ce même un ensemble? Parce qu'il a une règle non ambiguë pour déterminer quels éléments appartiennent à \(E\): Un nombre réel \(x\) appartient à \(E\) s'il est divisible par 2. La règle fonctionne sans ambiguïté pour chaque nombre réel unique déterminant s'il appartient ou non à \(E\). Pourquoi je dis «sans ambiguïté» et je le répète sans cesse. Parce que c'est important. Cela signifie sans ambiguïté qu'il n'y a aucun moyen de conclure qu'un \(x\) donné appartient et n'appartient pas à \(E\). Malheureusement, les choses dépassent parfois notre imagination. Contrairement à notre intuition, un ensemble définissable avec une simple règle d'appartenance peut conduire à une classification d'appartenance ambiguë (contradictoire), comme l'a montré Bertrand Russell dans son célèbre paradoxe. Russell a montré qu'une définition plus précise de ce qu'est un ensemble devrait être utilisée.

À toutes fins pratiques, nous penserons un ensemble comme une collection d'éléments, définissable par une règle d'appartenance .

QUEL EST LE PRODUIT DE DEUX ENSEMBLES?

Soit \(A\) et \(B\) des ensembles, dans le cadre de la définition donnée ci-dessus. Le produit \(A\times B\) de deux ensembles est un autre ensemble, qui est défini comme l'ensemble de toutes les paires ordonnées possibles de la forme \(\left( a, b \right)\), où \(a\) appartient à \(A\) et \(b\) appartient à \(B\). Donc, \(A\times B\) est un ensemble, et ses éléments sont des paires ordonnées de la forme \(\left( a ,b \right)\). Ne laissez pas cette notation vous impressionner. Quand je dis «paires ordonnées de la forme \(\left( a, b \right)\)», le symbole \(\left( a, b \right)\) est un symbole composé, pour indiquer un élément qui est composé de deux entités \(a\) et \(b\), et identifier le premier élément comme étant \(a\), et le deuxième élément comme étant \(b\) . C'est tout. Au lieu de \(\left( a,b \right)\), nous aurions pu choisir le symbole \(a\_b\), et cela aurait bien fonctionné.

Vous allez devoir me pardonner, mais je dois écrire la définition mathématique du produit de deux ensembles (on peut multiplier les ensembles aussi…. Qu'avez-vous pensé, on s'arrêterait avec des nombres seulement, euh?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

La raison pour laquelle j'écris la définition est que vous la regardiez et que vous reconnaissiez comment, en utilisant une notation très compacte, nous disons exactement la même manière que je l'ai définie avec des mots dans le paragraphe ci-dessus. J'espère que vous relâcherez votre peur de lire des déclarations mathématiques. Les mathématiciens peuvent parfois être des gens géniaux, mais ils trouvent de bonnes notations, claires et compactes. Et par conséquent, le langage mathématique est SUPER facile à lire. Droite? Droite? Dites-moi que j'ai raison…

Une note latérale, pour des raisons historiques, le produit de deux ensembles \(A\times B\) est normalement appelé produit cartésien .

MAINTENANT, LA DÉFINITION D'UNE FONCTION (ENFIN)

Ok, j'ai menti, il reste une étape avant de définir ce qu'est une fonction. Nous devons définir le concept de relation . Qu'est-ce qu'une relation? Au-delà de son utilisation courante en tant que mot anglais, une relation est simplement un sous-ensemble d'un produit cartésien. TOUT sous-ensemble d'un produit cartésien est une relation. Donc, si \(A\) et \(B\) sont des ensembles, un ensemble \(R\) est une relation si \(R\subseteq A\times B\). Puisque tout ensemble peut être considéré comme un sous-ensemble de lui-même, tous les produits cartésiens sont eux-mêmes des relations.

Mettez-le sur un cadre:

Une relation est un ensemble qui est un sous-ensemble d'un produit cartésien

Soyons plus graphiques. Considérez l'ensemble \(A=\left[ 0,1 \right]\) (qui est tous les nombres réels qui sont supérieurs ou égaux à 0, et ils sont également inférieurs ou égaux à 1). Quel est le produit cartésien \(A\times A\)? Parrot ce que nous venons d'apprendre. Le produit cartésien \(A\times A\) est \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) dans ce cas est l'ensemble de toutes les paires\(\left( x, y \right)\), où \(x\) et \(y\) appartiennent à \(\left[ 0,1 \right]\). Les produits cartésiens sont généralement faciles à représenter graphiquement. Regardez la région ombrée ci-dessous:

Maintenant, qu'est-ce qui ferait une relation? Nous pouvons «découper» tout ce que nous voulons dans la région ombrée ci-dessus, et ce qui reste est une relation dans \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Par exemple, nous pouvons couper les «coins» pour obtenir la sous-région suivante:

La région (ensemble) ci-dessus est une relation. Pourquoi? Parce que c'est un sous-ensemble du produit cartésien \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Mais nous pouvons faire encore plus. Que diriez-vous de découper un quart de cercle? Voir la région ci-dessous.

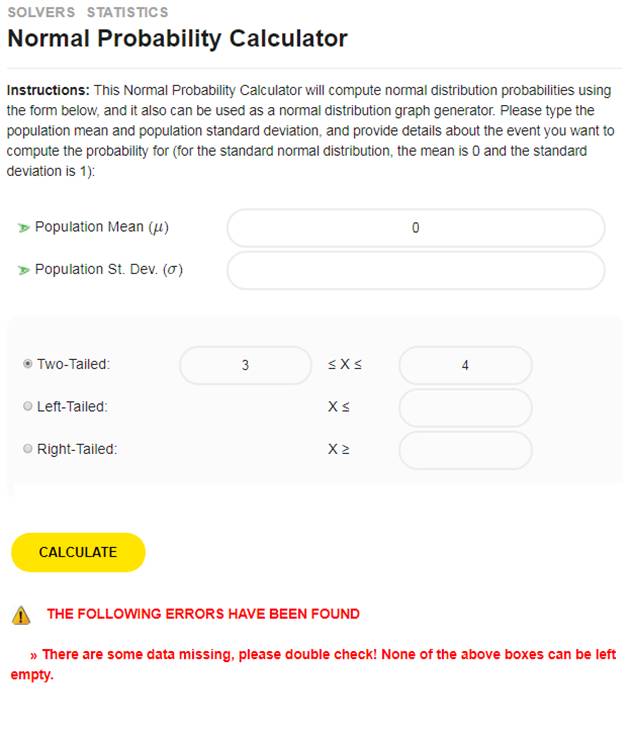
La région (ensemble) ci-dessus est une relation. Pourquoi? Encore une fois, car il s'agit d'un sous-ensemble du produit cartésien \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

Maintenant, laissez-moi vous donner un exemple de deux relations dans \(\left[ -1,1 \right]\times \left[ -1,1 \right]\). Voir les graphiques ci-dessous:

Relation 1

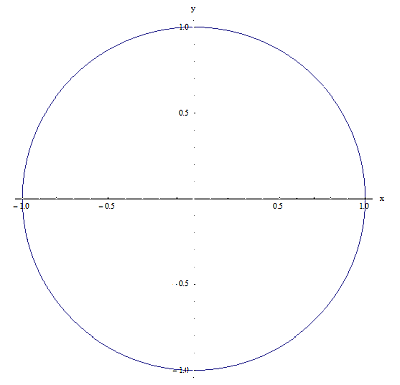
Relation 2

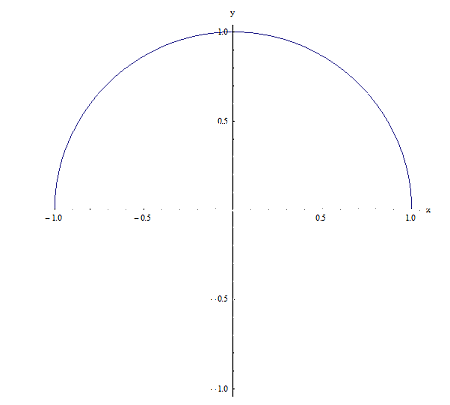
Ce sont tous les deux évidemment des relations (car ils sont tous deux contenus dans le produit cartésien \(\left[ -1,1 \right]\times \left[ -1,1 \right]\), mais ils ont une différence clé: Pour la relation 1, pour un point x donné sur \(\left[ -1,1 \right]\), il y a deux points \({{y}_{1}}\) et \({{y}_{2}}\) qui ont la propriété d'appartenir \(\left( x,{{y}_{1}} \right)\) et \(\left( x,{{y}_{2}} \right)\) à la relation 1. Par exemple pour x = 0, il y a deux points \({{y}_{1}}=1\) et \({{y}_{2}}=-1\) tels que \(\left( 0,1 \right)\) et\(\left( 0,-1 \right)\) appartiennent à la relation 1. Or, pour la relation 2 ce n'est pas le cas car, par exemple, pour x = 0 ce n'est que \(y=1\) qui fait que le point \(\left( 0,1 \right)\) appartient à la relation 1.

Enfin, nous pouvons définir une fonction: Une fonction \(R\) est un ensemble qui est une relation et elle a également la propriété que si le point \(\left( x,y \right)\) appartient à \(R\), alors il n'y a pas d'autre point \(\bar{y}\) différent de \(y\) qui a la propriété que \(\left( x,\bar{y} \right)\) appartient à \(R\) ainsi que. En d'autres termes, une fonction est une relation avec l'exigence supplémentaire que chaque \(x\) dans son domaine est associé à un seul \(y\).

Comment savoir différencier une fonction et une relation?

Gadgets! Nous utilisons une petite astuce appelée «Test de ligne verticale»: Nous dessinons une ligne verticale imaginaire, et nous la balançons en la déplaçant de gauche à droite tout le long, et en créant une carte mentale de l'endroit où la ligne verticale coupe la relation.

• Si à N'IMPORTE QUEL point, la ligne verticale coupe la relation en PLUS d'un point, alors la relation échoue au test de la ligne verticale, et alors la relation n'est pas une fonction

• Si à N'IMPORTE QUEL point, la ligne verticale ne coupe la relation nulle part en PLUS d'un point, alors la relation passe le test de la ligne verticale, puis la relation est une fonction

Voir les deux exemples ci-dessous:

Exemple 1: il échoue au test de la ligne verticale car la ligne verticale montrée sur la figure coupe la relation en plusieurs points: PAS UNE FONCTION

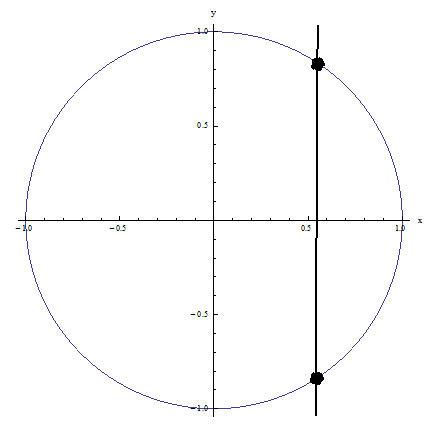
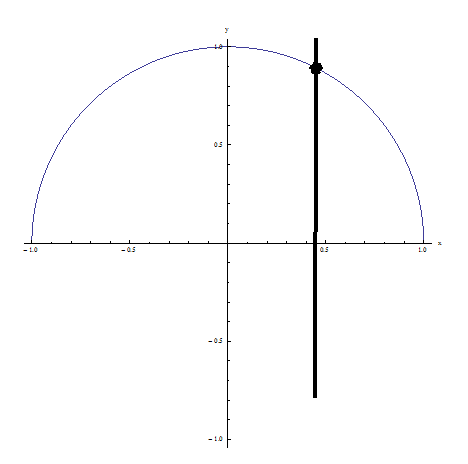
Exemple 2: Il réussit le test de la ligne verticale car aucune ligne verticale ne coupe la relation en plus d'un point: C'EST UNE FONCTION!

Il existe de nombreuses applications graphiques qui peuvent être réalisées avec des fonctions, y compris le calcul de asymptotes horizontales , asymptotes verticales et asymptotes obliques le cas échéant.