Zéros polynomiaux

Cette calculatrice vous permet de calculer les racines de tout polynôme valide que vous fournissez. Ce polynôme peut être n'importe quel polynôme de degré 1 ou plus.

Par exemple, vous pouvez fournir un polynôme cubique, tel que p(x) = x^3 + 2x^2 - x + 1, ou vous pouvez fournir un polynôme avec des coefficients non entiers, tel que p(x) = x^3 - 13/12 x^2 + 3/8 x - 1/24.

Une fois que vous avez fourni à la calculatrice un polynôme valide dont vous voulez calculer les racines, vous pouvez cliquer sur le bouton "Calculer", et vous verrez un déroulement pas à pas du processus.

Il est nécessaire de mentionner que le processus n'implique que des méthodes élémentaires utilisées pour trouver des racines, ce qui comprend les éléments suivants Théorème du zéro rationnel et Division polynomiale ainsi que l'utilisation de la formule quadratique le cas échéant.

Il n'existe pas de méthode générale pour trouver TOUTES les racines de TOUS les polynômes possibles de degré au-dessus de 5, donc cette calculatrice ne trouvera que les racines qui peuvent être obtenues avec les méthodes élémentaires mentionnées.

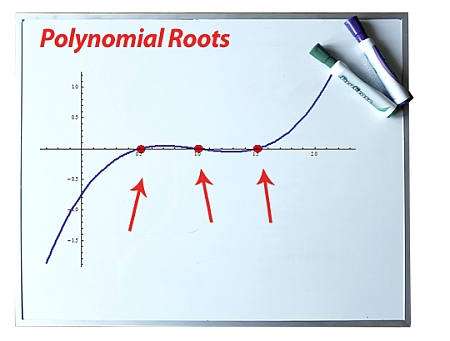
Quelle est la racine d'un polynôme ?

Étant donné un fonction polynomiale \(p(x)\), on dit que \(x\) est une racine du polynôme si :

\[\displaystyle p(x) = 0 \]

En termes simples, les racines d'un polynôme sont les points où la fonction polynomiale \(p(x)\) croise l'axe des abscisses. C'est une bonne représentation pour se faire une idée, mais elle n'est pas complètement précise car certaines racines pourraient être des nombres complexes. Ainsi donc, une racine réelle sera un point où \(p(x)\).

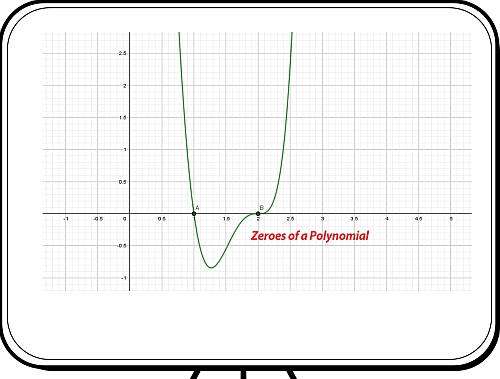
Observez que les racines du polynôme sont également appelées zéros du polynôme.

Quelles sont les étapes pour trouver les zéros d'un polynôme ?

• Étape 1: Identifiez l'expression avec laquelle vous voulez travailler. Assurez-vous qu'il s'agit d'un polynôme et simplifiez autant que possible
• Étape 2: Nous utiliserons le factorisation polynomiale approche pour trouver sa racine
• Étape 3: Commencez à essayer de trouver des racines élémentaires (rationnelles) avec la fonction Théorème du zéro rationnel et utiliser Division polynomiale pour réduire le polynôme d'origine, si possible
• Étape 4: Si l'étape 3 a fonctionné et que vous avez pu réduire le polynôme d'origine, répétez les étapes précédentes pour essayer de factoriser le polynôme réduit

Ce n'est généralement pas facile, cela peut demander beaucoup de calculs et il n'est pas garanti que cela fonctionne, mais c'est la meilleure approche possible si nous sommes limités à l'utilisation de méthodes élémentaires.

La factorisation est-elle le seul moyen de trouver des racines

Pas vraiment, mais les choses vont de pair. Le site théorème des facteurs stipule que \(x - a\) est un facteur d'un polynôme \(p(x)\) si et seulement si \(p(a) = 0\). En d'autres termes, racines et facteurs sont intimement liés.

Maintenant, pour les polynômes de degré 2 (c'est-à-dire, polynômes quadratiques ), nous pouvons utiliser une formule explicite, qui est la formule bien connue suivante formule quadratique .

Il en va de même pour les degrés 3 et 4, bien que les formules soient loin d'être élémentaires. Mais pour les degrés 5 et plus, une telle formule n'existe pas, un résultat clé prouvé par Galois et Abel. Il n'y a donc aucun espoir de trouver une "formule générale", et c'est pourquoi on utilise une formule plus laxiste factorisation polynomiale approche.

Les erreurs courantes à éviter

Souvent, les étudiants sont frustrés de ne pas pouvoir trouver les racines d'un problème donné fonction polynomiale mais ils doivent faire face au fait que tous les polynômes ne pourront pas être résolus à l'aide des outils élémentaires.

Certes, il existe une formule pour résoudre \(x^3+2 x^2-x+1 = 0 \), mais elle n'est pas élémentaire et on ne s'attend pas à ce que les élèves la connaissent.

Conseils pour réussir

Essayez toujours de faire une carte mentale de ce que sera votre stratégie : Notez le polynôme que vous avez, son degré, son coefficient principal et son coefficient constant.

Tracez le polynôme si vous le pouvez, pour avoir une idée de son comportement. Y a-t-il une factorisation évidente que vous pouvez utiliser ? Utilisez-les. Rappelez-vous toujours que facteurs = racines.

Exemple : zéros d'un polynôme

Quels sont les zéros de : \(x^5 + x^4 - x^3 + x^2 - x + 1\) ?

Solution: Pour cet exemple, on nous fournit le polynôme suivant : \(\displaystyle p(x) = x^5+x^4-x^3+x^2-x+1\). Nous allons utiliser l'approche de la factorisation pour trouver les racines.

La simplification n'est pas nécessaire : L'expression polynomiale fournie est déjà simplifiée, il n'y a donc pas lieu de la simplifier davantage.

On peut noter que le degré du polynôme fourni est \(\displaystyle deg(p) = 5\). De plus, son coefficient directeur est \(\displaystyle a_{5} = 1\) et son coefficient constant est égal à\(\displaystyle a_0 = 1\).

Nous recherchons maintenant les nombres entiers qui divisent le coefficient principal \(a_{5}\) et le coefficient constant \(a_0\), qui est utilisé pour trouver des candidats rationnels .

▹ Les diviseurs de \(a_{5} = 1\) sont : \(\pm 1\).

▹ Les diviseurs de \(a_0 = 1\) sont : \(\pm 1\).

Par conséquent, en divisant tous les facteurs du terme constant \(a_0 = 1\) par tous les diviseurs de \(a_{5} = 1\), on obtient la liste suivante de racines potentielles :

\[\pm \frac{ 1}{ 1}\]

Il faut maintenant évaluer toutes les solutions potentielles. Les résultats obtenus en testant chaque candidat sont les suivants :

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle \left(-1\right)^5+\left(-1\right)^4-\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+1 & = & \displaystyle 4 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^5+1^4-1^3+1^2-1+1 & = & \displaystyle 2 \ne 0 \\\\ \end{array}\]

Puisqu'aucune racine rationnelle n'a été identifiée par l'inspection manuelle, une simplification supplémentaire à l'aide des techniques de base n'est pas possible et le processus se termine avec cette étape.

Conclusion : En conséquence, aucune simplification n'a été obtenue et aucune racine du polynôme n'a été identifiée par les techniques de base

Exemple : calcul des racines d'une fonction quadratique

Calculez les solutions de : \(3x^2 - 2x - 4 = 0\).

Solution: Nous devons résoudre l'équation quadratique donnée \(\displaystyle 3x^2-2x-4=0\).

Les racines d'une équation quadratique de la forme \(a x^2 + bx + c = 0\) sont calculées à l'aide de l'équation suivante :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Dans ce contexte, l'équation qui doit être résolue est \(\displaystyle 3x^2-2x-4 = 0\), indiquant que les coefficients correspondants sont :

\[a = 3\] \[b = -2\] \[c = -4\]

Dans un premier temps, nous allons déterminer la nature des racines en calculant le discriminant. Le discriminant se calcule comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(3\right)\cdot \left(-4\right) = 52\]

Puisque dans ce cas, nous obtenons le discriminant est \(\Delta = \displaystyle 52 > 0\), qui est positif, donc alors, l'équation a deux racines réelles différentes.

On en déduit :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(3\right)\left(-4\right)}}{2\cdot 3} = \displaystyle \frac{2 \pm \sqrt{52}}{6}\]

donc, nous trouvons que :

\[ x_1 = \frac{2}{6}-\frac{1}{6}\sqrt{52}=\frac{2}{6}-\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}-\frac{1}{3}\sqrt{13}=\frac{1}{3}-\frac{1}{3}\sqrt{13} \] \[x_2 = \frac{2}{6}+\frac{1}{6}\sqrt{52}=\frac{2}{6}+\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}+\frac{1}{3}\sqrt{13}=\frac{1}{3}+\frac{1}{3}\sqrt{13}\]

On trouve que l'équation \( \displaystyle 3x^2-2x-4 = 0 \), a deux racines réelles, donc alors :

\[\displaystyle 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

alors le polynôme original est factorisé comme \(\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right) \), ce qui complète la factorisation.

Conclusion : Par conséquent, la factorisation que nous cherchons est donnée par :

\[\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

Les racines trouvées sont \(-\frac{1}{3}\sqrt{13}+\frac{1}{3}\) et \(\frac{1}{3}\sqrt{13}+\frac{1}{3}\) .

Exemple : zéros de polynômes

Calculez les zéros du polynôme suivant : \(p(x)= x^3 - \frac{13}{12} x^2 + \frac{3}{8} x - \frac{1}{24} \).

Solution: Enfin, dans cet exemple, nous avons : \(\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24}\).

Première Étape : L'expression polynomiale fournie est irréductible, il n'y a donc rien à simplifier. Nous pouvons procéder à sa factorisation.

Observez que le degré du polynôme donné est \(\displaystyle deg(p) = 3\), son coefficient directeur est \(\displaystyle a_{3} = 1\) et son coefficient constant est \(\displaystyle a_0 = -\frac{1}{24}\).

Racines Rationnelles : Nous allons d'abord essayer de trouver des racines rationnelles simples, avec le théorème du zéro rationnel.

La tâche suivante consiste à trouver les nombres entiers qui divisent le coefficient principal \(a_{3}\) et le coefficient constant \(a_0\), qui seront utilisés pour construire nos candidats aux zéros de l'équation polynomiale.

Note : Dans ce cas, nous observons que pour avoir à la fois un coefficient constant et un coefficient directeur, nous devons amplifier les deux côtés de l'équation par \(24\). L'équation équivalente est la suivante :

\[24x^3-26x^2+9x-1 = 0\]

▹ Les diviseurs de \(a_{3} = 24\) sont : \(\pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 8,\pm 12,\pm 24\).

▹ Les diviseurs de \(a_0 = -1\) sont : \(\pm 1\).

Par conséquent, en divisant chaque diviseur du coefficient constant \(a_0 = -1\) par chaque diviseur du coefficient principal \(a_{3} = 24\), nous trouvons la liste suivante de candidats aux racines :

\[\pm \frac{ 1}{ 1},\pm \frac{ 1}{ 2},\pm \frac{ 1}{ 3},\pm \frac{ 1}{ 4},\pm \frac{ 1}{ 6},\pm \frac{ 1}{ 8},\pm \frac{ 1}{ 12},\pm \frac{ 1}{ 24}\]

Maintenant, tous les candidats doivent être testés pour voir s'ils constituent une solution. Les résultats suivants sont obtenus en testant chaque candidat :

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle 24\cdot \left(-1\right)^3-26\cdot \left(-1\right)^2+9\cdot \left(-1\right)-1 & = & \displaystyle -60 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 24\cdot 1^3-26\cdot 1^2+9\cdot 1-1 & = & \displaystyle 6 \ne 0 \\\\ x & = & \displaystyle -\frac{1}{2} &:&    & \displaystyle 24\left(\frac{-1}{2}\right)^3-26\left(\frac{-1}{2}\right)^2+9\left(-\frac{ 1}{ 2}\right)-1 & = & \displaystyle -15 \ne 0 \\\\ x & = & \displaystyle \frac{1}{2} &:&    & \displaystyle 24\left(\frac{1}{2}\right)^3-26\left(\frac{1}{2}\right)^2+9\cdot \frac{1}{2}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{3} &:&    & \displaystyle 24\left(\frac{-1}{3}\right)^3-26\left(\frac{-1}{3}\right)^2+9\left(-\frac{ 1}{ 3}\right)-1 & = & \displaystyle -\frac{70}{9} \ne 0 \\\\ x & = & \displaystyle \frac{1}{3} &:&    & \displaystyle 24\left(\frac{1}{3}\right)^3-26\left(\frac{1}{3}\right)^2+9\cdot \frac{1}{3}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{4} &:&    & \displaystyle 24\left(\frac{-1}{4}\right)^3-26\left(\frac{-1}{4}\right)^2+9\left(-\frac{ 1}{ 4}\right)-1 & = & \displaystyle -\frac{21}{4} \ne 0 \\\\ x & = & \displaystyle \frac{1}{4} &:&    & \displaystyle 24\left(\frac{1}{4}\right)^3-26\left(\frac{1}{4}\right)^2+9\cdot \frac{1}{4}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{6} &:&    & \displaystyle 24\left(\frac{-1}{6}\right)^3-26\left(\frac{-1}{6}\right)^2+9\left(-\frac{ 1}{ 6}\right)-1 & = & \displaystyle -\frac{10}{3} \ne 0 \\\\ x & = & \displaystyle \frac{1}{6} &:&    & \displaystyle 24\left(\frac{1}{6}\right)^3-26\left(\frac{1}{6}\right)^2+9\cdot \frac{1}{6}-1 & = & \displaystyle -\frac{1}{9} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{8} &:&    & \displaystyle 24\left(\frac{-1}{8}\right)^3-26\left(\frac{-1}{8}\right)^2+9\left(-\frac{ 1}{ 8}\right)-1 & = & \displaystyle -\frac{165}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{8} &:&    & \displaystyle 24\left(\frac{1}{8}\right)^3-26\left(\frac{1}{8}\right)^2+9\cdot \frac{1}{8}-1 & = & \displaystyle -\frac{15}{64} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{12} &:&    & \displaystyle 24\left(\frac{-1}{12}\right)^3-26\left(\frac{-1}{12}\right)^2+9\left(-\frac{ 1}{ 12}\right)-1 & = & \displaystyle -\frac{35}{18} \ne 0 \\\\ x & = & \displaystyle \frac{1}{12} &:&    & \displaystyle 24\left(\frac{1}{12}\right)^3-26\left(\frac{1}{12}\right)^2+9\cdot \frac{1}{12}-1 & = & \displaystyle -\frac{5}{12} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{24} &:&    & \displaystyle 24\left(\frac{-1}{24}\right)^3-26\left(\frac{-1}{24}\right)^2+9\left(-\frac{ 1}{ 24}\right)-1 & = & \displaystyle -\frac{91}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{24} &:&    & \displaystyle 24\left(\frac{1}{24}\right)^3-26\left(\frac{1}{24}\right)^2+9\cdot \frac{1}{24}-1 & = & \displaystyle -\frac{385}{576} \ne 0 \\\\ \end{array}\]

Mais comme nous avons trouvé toutes les racines requises parmi les candidats rationnels, nous trouvons que \(\displaystyle x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \), donc alors :

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \]

ce qui termine le processus de factorisation.

Résultat : Par conséquent, la factorisation finale est :

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right)\]

Par conséquent, les racines trouvées sont \(\frac{1}{2}\),\(\frac{1}{3}\) et \(\frac{1}{4}\) .

Autres calculateurs de polynômes utiles

Trouver les zéros d'un polynôme est l'un des sommets de l'algèbre, dans la mesure où le théorème fondamental de l'algèbre concerne l'existence de n racines pour un polynôme de degré n. Ces racines ne seront pas nécessairement toutes réelles, et certaines d'entre elles (ou toutes) peuvent être des nombres compexes.

En fin de compte, presque tous les problèmes d'algèbre et de calcul peuvent être réduits à la recherche des racines d'un polynôme, y compris la résolution des problèmes suivants équations polynomiales comme celles que l'on trouve, par exemple, lorsqu'on cherche le intersection entre les graphes de \(y = x^2\) et \(y = x^3\).