Solveurs Algèbre

Fonctions polynomiales

Instructions: Utilisez cette calculatrice de fonction polynomiale pour calculer une opération algébrique impliquant des polynômes. Tapez une expression qui implique une opération avec des polynômes, et la calculatrice le fera, simplifiera le résultat et vous donnera le graphique, en vous montrant toutes les étapes.

Fonctions polynomiales

Cette calculatrice de fonctions polynomiales vous aidera à calculer les fonctions polynomiales, en calculant et en simplifiant toute expression polynomiale que vous lui fournirez.

Vous pouvez fournir n'importe quel type d'expression impliquant des polynômes, et le calcul sera effectué et les étapes de simplification nécessaires seront prises, afin de laisser une fonction polynomiale dans sa forme la plus compacte. Ensuite, un graphique polynomial sera fourni

Ensuite, une fois qu'une expression polynomiale valide a été fournie, vous pouvez cliquer sur le bouton ci-dessous, le bouton "Calculer", et toutes les étapes requises du processus seront affichées.

L'algèbre des fractions implique la conversion des fractions, comme l'utilisation du dénominateur commun, et l'utilisation des règles arithmétiques de base. Dans l'ensemble, le processus de calcul peut être laborieux, bien qu'il puisse être effectué de manière systématique, sans grand problème.

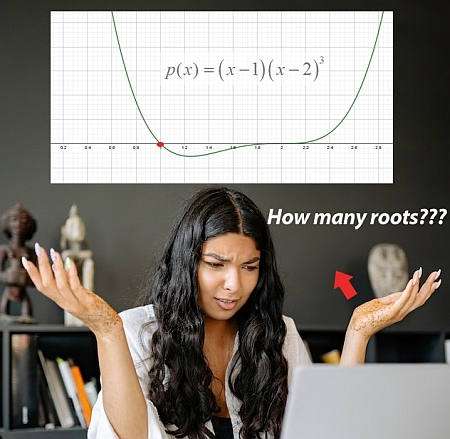
Qu'est-ce qu'une fonction polynomiale ?

Les polynômes, dans l'explication la plus simple, sont les fonctions qui ne sont constituées que de puissances de $x$, éventuellement multipliées par des constantes numériques, qui sont ajoutées (ou soustraites) les unes aux autres. Par exemple, $p(x) = x^3 + 2x^2 + 1$ est une fonction polynomiale, puisqu'elle est constituée des puissances de $x$ multipliées par des constantes, additionnées entre elles. Dans ce cas, $1 = x^0$ donc une constante est également une puissance de $x$... :

En général, une fonction polynomiale a la forme suivante :

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

avec $a_n \ne 0$. Dans ce cas, on dit que le degré du polynôme (ou son ordre) est $n$, qui est la plus grande puissance présente dans la fonction polynomiale.

Aussi, le coefficient $a_n$ est appelé le coefficient dominant et $a_n x^n$ est appelée la premier mandat . Le coefficient directeur et le degré d'un polynôme déterminent son comportement final (c'est-à-dire son comportement lorsque la valeur absolue de x est grande).

Quelles sont les étapes à suivre pour travailler avec une fonction polynomiale ?

Étape 1: Identifiez clairement l'expression avec laquelle vous voulez travailler, élargissez et simplifiez
Étape 2: Vérifier si les termes qui font intervenir la variable x ne correspondent qu'à des puissances de x, sinon on s'arrête, ce n'est pas un polynôme
Étape 3: Assurez-vous que toutes les puissances de x sont multipliées par des constantes (qui peuvent être '1'), et que ces termes apparaissent comme ajoutés ou soustraits dans l'expression

Il est important de s'assurer que vous disposez d'une fonction polynomiale, afin de pouvoir appliquer les résultats exclusifs aux polynômes, tels que l'a théorème des facteurs , la théorème du reste et le Théorème du zéro rationnel qui sont extrêmement utiles pour trouver les solutions des équations polynomiales, qui sont largement utilisées dans différentes applications.

De plus, l'avantage de traiter avec des fonctions polynomiales est que vous pouvez facilement réaliser division de polynômes soit en utilisant Division longue , ou Division synthétique dans le cas où le diviseur est linéaire.

Existe-t-il des fonctions polynomiales importantes ?

En effet. Il existe les fameux polynômes de degré 2, que nous appelons polynômes quadratiques qui sont largement étudiées en algèbre de base. La raison en est qu'elles peuvent être entièrement analysées à l'aide de formules précises. Par exemple, vous avez un formule pour le sommet et la célèbre formule quadratique est utilisée pour trouver les racines de polynômes quadratiques :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Il y a aussi les polynômes de degré 2, que nous appelons polynômes cubiques qui ont également des formules explicites, mais qui sont généralement considérées comme plus complexes et qui ne sont pas abordées dans les cours d'algèbre de base.

Que sais-je du comportement final d'un polynôme ?

Le comportement final d'un polynôme dépend en fin de compte du polynôme lui-même, mais on peut dire quelques choses sur la base de leur degré

Fait 1 : Pour les polynômes quadratiques, le graphique s'ouvre vers le haut (si le coefficient principal est positif) ou vers le bas (si le coefficient principal est négatif), et la fonction converge vers l'infini ou l'infini négatif (selon le signe du coefficient principal) des deux côtés
Fait 2 : Pour les polynômes dont le degré est impair (par exemple, de degré 3), il y aura au moins une racine réelle, et la fonction converge vers l'infini d'un côté, et vers moins l'infini de l'autre côté
Fait 3 : Pour les polynômes de degré pair (par exemple, de degré 4), il n'y aura pas nécessairement de racines réelles (un point que le graphique croise sur l'axe des x), et la fonction converge vers l'infini ou l'infini négatif (selon le signe du coefficient principal) des deux côtés

Ainsi, les polynômes sont grands pour les grandes valeurs de x, et le fait que leurs valeurs soient positives ou négatives pour les valeurs positives de x (dans leur comportement final) dépend du signe du coefficient principal.

Conseils : quels sont les avantages de l'utilisation d'une calculatrice de fonctions polynomiales ?

Les calculatrices polynomiales peuvent vous assurer que vous arrivez à la bonne réponse. En effet, calculs polynomiaux ne sont pas compliquées, mais elles peuvent être lourdes et il n'est pas difficile de faire des erreurs.

Évitez les erreurs algébriques en vérifiant votre travail avec cette calculatrice, afin de vous assurer de la cohérence de la réponse finale et des étapes utilisées pour y parvenir.

Exemple : fonction polynomiale

Calculez la fonction polynomiale suivante $(x-3)(x-1)(x-4)$

Solution: On nous fournit l'expression polynomiale suivante que nous devons calculer : $\displaystyle (x-3)(x-1)(x-4)$.

On obtient le calcul suivant :

$ \displaystyle \left(x-3\right)\left(x-1\right)\left(x-4\right)$

Observe that $(x-3) \cdot (x-1) = x^2-1x-3x+3\cdot 1 = x^2-4x+3$, as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \left(x^2-4x+3\right)\left(x-4\right)$

Observe that $(x^2-4x+3) \cdot (x-4) = x^2x-4x^2-4x^2+4\cdot 4x+3x-3\cdot 4 = x^3-8x^2+19x-12$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle x^3-8x^2+19x-12$

ce qui conclut le processus de simplification polynomiale.

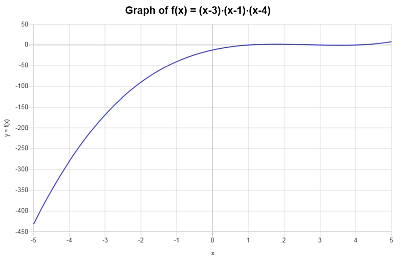
Le tracé suivant est obtenu pour $\displaystyle x^3-8x^2+19x-12$ sur l'intervalle $[-5, 5]$ :

Exemple : calcul d'une fonction polynomiale

Est-ce une fonction polynomiale : $\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})$

Solution:

On nous fournit l'expression polynomiale suivante que nous devons calculer : $\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})$.

On obtient le calcul suivant :

$ \displaystyle \frac{1}{3}x^3+\frac{5}{4}\left(x-3\right)\left(x-\frac{5}{6}\right)$

We get that $(x-3) \cdot (x-\frac{5}{6}) = x^2-\frac{5}{6}x-3x+3\cdot \frac{5}{6} = x^2-\frac{23}{6}x+\frac{5}{2}$, as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \frac{1}{3}x^3+\frac{5}{4}\left(x^2-\frac{23}{6}x+\frac{5}{2}\right)$

We get that $(\frac{5}{4}) \cdot (x^2-\frac{23}{6}x+\frac{5}{2}) = \frac{5}{4}x^2-\frac{5}{4}\cdot \frac{23}{6}x+\frac{5}{2}\cdot \frac{5}{4} = \frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}$, by using the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}$

ce qui met fin au processus de simplification.

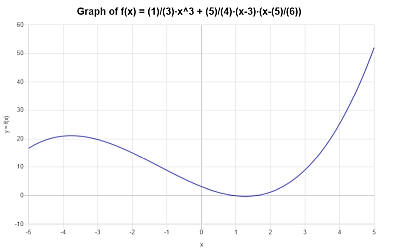
Graphiquement, on obtient pour la fonction simplifiée $\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}$ sur l'intervalle $[-5, 5]$ ce qui suit :

Un Autre Exemple De Fonction Polynomiale

Exemple : utilisation d'une calculatrice polynomiale

Calculez $ x^2 - (2x - 1)x $.

Solution: Dans ce dernier exemple, nous avons $\displaystyle x^2 - (2x - 1)x $, que nous devons simplifier.

On obtient le calcul suivant :

$ \displaystyle x^2-\left(2x-1\right)x$

Notice that $(2x-1) \cdot (x) = 2x^2-1x = 2x^2-x$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle x^2-2x^2+x$

Putting together the terms with $x^2$

$ \displaystyle = \,\,$

$\displaystyle x+\left(1-2\right)x^2$

Operating the terms that were grouped with $x^2$

$ \displaystyle = \,\,$

$\displaystyle x-x^2$

ce qui met fin à la simplification.

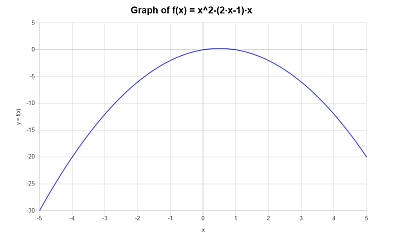
Le tracé suivant est obtenu pour $\displaystyle -x^2+x$ sur l'intervalle $[-5, 5]$ :

Plus D'Exemples De Fonctions Polynomiales

Plus de calculatrices d'algèbre

Les fonctions polynomiales sont littéralement la pièce maîtresse de l'algèbre. Pour les applications de base, polynômes quadratiques jouera un rôle clé ainsi que l'économie, la physique et l'ingénierie.

Les fonctions polynomiales ont des propriétés extrêmement puissantes, notamment en ce qui concerne le calcul de racines polynomiales qui ont une forte signification dans les applications.