Grapheur de fonctions trigonométriques

Les fonctions trigonométriques ont la propriété de répéter leur comportement. C'est-à-dire qu'elles sont périodiques. Mathématiquement, cela signifie qu'il existe un nombre \(P\) ayant la propriété que

\[f(x+P) = f(x)\]

pour toutes les valeurs de \(x\). Ce nombre \(P\) s'appelle le période . Tout ce que cela veut dire, c'est que le comportement de la fonction se répète dans les graphiques trigonométriques toutes les \(P\) unités sur l'axe des x.

Observez que dans toutes les fonctions trigonométriques que vous fournissez pour cette calculatrice, l'argument \(x\) est supposé être mesurée en radians .

Exemple de fonctions périodiques

Par exemple, pour le cas de la fonction sinus, \(f(x) = \sin x\), le graphique est présenté ci-dessous :

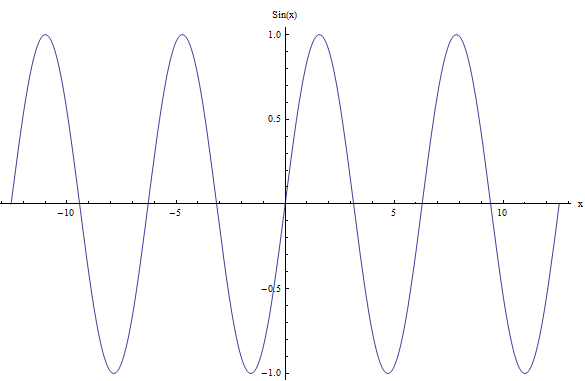
Vous pouvez voir que le comportement de la fonction se répète. En effet, vous pouvez prendre n'importe quel intervalle de longueur \(2\pi\) et l'intervalle suivant de longueur \(2\pi\) sera identique au précédent, en termes de forme de la fonction.

Pourquoi cela se produit-il ? Parce que \(\sin(x + 2\pi) = \sin(x)\), pour tout \(x\), et alors la fonction est périodique.

Que puis-je représenter graphiquement avec ce traceur de fonctions trigonométriques ?

Vous pouvez tracer n'importe quelle fonction trigonométrique. L'utilisation la plus courante est le graphique du sinus et du cosinus, mais vous pouvez l'utiliser pour toute fonction trigonométrique.

Vous verrez que les fonctions périodiques peuvent être rendues plus complexes en les combinant avec d'autres expressions algébriques.

Par exemple, quel est le comportement de la fonction \(f(x) = 3\sin(2x+1)-4\) Eh bien, elle est même périodique ? Oui, c'est sûr. Le comportement de la fonction \(f(x) = 3\sin(2x+1)-4\) est en tout point semblable à celui de la fonction \(f(x) = \sin x\).

Ce grapheur de fonctions trigonométriques vous aidera à trouver le graphe et les caractéristiques spécifiques (période, fréquence, amplitude, déphasage et décalage vertical) de fonctions trigonométriques plus complexes, telles que \(f(x) = 3\cos(\pi(x-2)+3)-\frac{\pi}{4}\)

Les parenthèses sont-elles importantes ?

En bref, la réponse est : cela dépend. Parfois, vous aurez une expression simple dans laquelle seules des sommes ou des multiplications sont présentes, auquel cas l'option propriété associative peut être utilisé. Mais lorsqu'il y a des opérations mixtes très fréquentes, on ne peut pas omettre ou modifier une parenthèse sans casser la fonction ou la modifier.

Calculatrices graphiques

Ce grapheur ne traite que des fonctions trigonométriques. Afin de graphiques d'autres fonctions vous pouvez utiliser notre traceur de fonctions générales qui prend n'importe quelle fonction, et pas seulement les fonctions trigonométriques.

Exemple de graphique trigonométrique

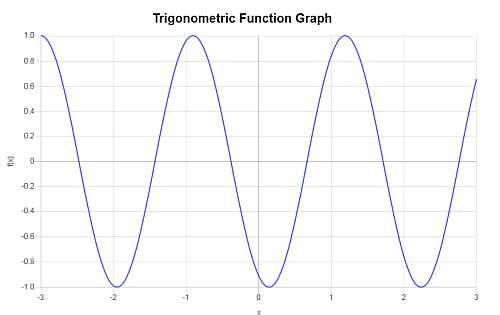
Question : Considérons la fonction \(f(x) = \sin(3x-2)\). Trouvez la période, la fréquence, l'amplitude et le déphasage. Fournissez également un graphique de la fonction.

Solution:

La fonction suivante a été prévue :

\[f(x) = \sin\left(3x-2\right)\]

Sur la base de l'argument de la fonction trigonométrique qui a été passé, la fréquence et la période sont calculées comme suit :

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

et aussi

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

En se basant sur la fonction trigonométrique fournie, \(f(x) = \sin\left(3x-2\right)\), on obtient que :

- L'amplitude dans ce cas est \(A = 1\).

- Le déphasage est égal à \(\displaystyle\frac{2}{3} = 0.6667\).

- Le décalage vertical est égal à \( 0\).

Sur la base des informations ci-dessus, on obtient le graphique suivant :