En savoir plus sur cet outil de calcul des probabilités de distribution normale

Voici quelques informations sur la probabilité de distribution normale afin que vous puissiez mieux comprendre ce générateur de graphique de distribution normale. Tout d'abord, la probabilité normale est un type de distribution de probabilité continue qui peut prendre des valeurs aléatoires sur toute la ligne réelle. Les principales propriétés de la distribution normale sont les suivantes

• Il est continu (et par conséquent, la probabilité d'obtenir un résultat unique et spécifique est nulle)


• Sa distribution est en forme de cloche (d'où le nom de "courbe en cloche")


• La distribution normale est déterminée par deux paramètres : la moyenne de la population et l'écart-type de la population


• Elle est symétrique par rapport à sa moyenne

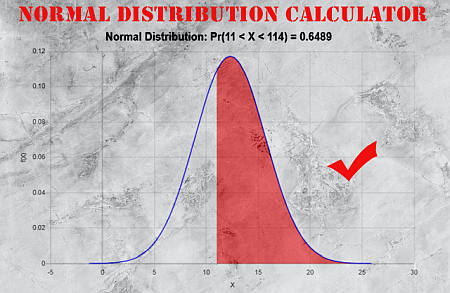
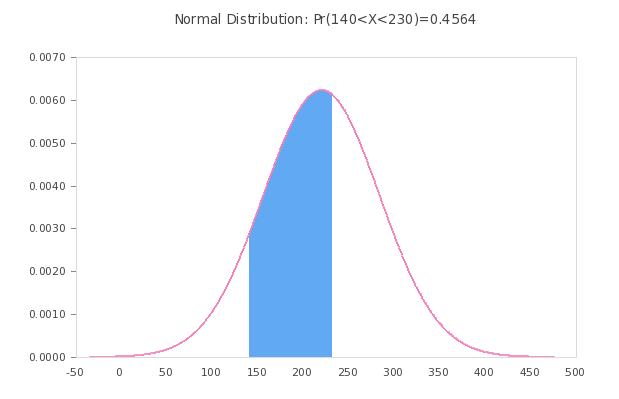
En utilisant ce qui précède calculatrice de courbe de distribution normale nous sommes en mesure de calculer des probabilités de la forme \(\Pr(a \le X \le b)\), ainsi que leurs valeurs respectives graphiques de distribution normale . Il ne s'agit pas exactement d'un calculatrice de la densité de probabilité normale il s'agit d'une calculatrice de distribution normale (cumulative). Modifiez les paramètres de a et b pour représenter graphiquement la distribution normale en fonction de vos besoins de calcul. Si vous devez calculer \(\Pr(3 \le X \le 4)\), vous taperez "3" et "4" dans les cases correspondantes du script.

Un cas particulier très important est celui de la Distribution normale standard ce qui correspond au cas d'une distribution normale avec une moyenne égale à \(\mu = 0\) et un écart type égal à \(\sigma = 1\). Les cas d'une distribution normale régulière ou d'une distribution normale standard peuvent tous être traités à l'aide de la calculatrice de probabilités ci-dessus.

Paramètres de la distribution normale

Par conséquent, n'oubliez pas que la distribution normale est en général déterminée par sa moyenne et son écart-type. La moyenne peut être n'importe quel nombre réel et l'écart-type peut être n'importe quel nombre non négatif.

Mais en particulier, la distribution normale standard est une distribution normale qui a la propriété que la moyenne de la distribution normale standard est zéro et que l'écart-type de la distribution normale standard est 1.

N'hésitez pas à nous contacter si vous avez des questions concernant ce générateur de graphiques de distribution normale.

Lien avec la distribution normale et le cdf normal

Le cdf normal est l'abréviation de la fonction de distribution cumulative normale qui, pour une valeur donnée de \(z\), fournit la probabilité totale jusqu'à la valeur de la valeur donnée \(z\).

Vous pouvez utiliser ce calculatrice normalcdf pour calculer la probabilité cumulative que vous souhaitez, et cela revient à utiliser cette calculatrice de distribution normale avec la limite inférieure \(-\infty\) et la limite supérieure \(z\).

La distribution normale et les scores z

À bien des égards, on peut considérer la calculatrice de distribution normale comme une calculateur de probabilité de score z en raison de la manière dont nous calculons les probabilités normales en général, il n'y a pas de différence entre les probabilités normales et les probabilités normales.

En effet, lorsque vous disposez d'une distribution normale générale avec une moyenne \(\mu\) et \(\sigma\) comme distribution de X, et que vous souhaitez calculer \(P(a \le X\le b)\), vous utilisez en fait les z-scores :

\[P(a \le X\le b) = Pr\left(\frac{a-\mu}{\sigma} \le \frac{X-\mu}{\sigma} \le \frac{b-\mu}{\sigma} \right)\] \[ = Pr\left(z_a \le Z \le z_b \right)\]

En d'autres termes, au lieu de calculer la probabilité que X se situe entre a et b, vous calculez les scores z correspondants de a et b, que vous appelez \(z_a\) et \(z_b\), et vous calculez la probabilité que Z (une variable avec une distribution normale standard) se situe entre \(z_a\) et \(z_b\).

Autre calculateur de distribution normale

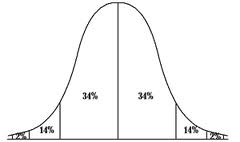
La distribution normale est une distribution continue cruciale. Outre cette calculatrice de distribution de probabilités pour les distributions normales, vous pouvez utiliser la calculatrice de distribution de probabilités pour les distributions normales calculateur de la règle 68-95-99 qui montre comment utiliser la règle empirique.

De plus, vous êtes souvent intéressé par le comportement des tailles d'échantillon, pour lequel vous pouvez utiliser notre calculatrice de distribution d'échantillonnage où vous prenez la moyenne d'échantillons de taille \(n\)

Autres distributions continues

Pour d'autres types de distributions continues, vous pouvez essayer par exemple.notre site propose de nombreux autres calculateurs de distributions continues tels que le calculatrice de distribution exponentielle . F calculatrice de distribution uniforme .