Calculatrice de division longue polynomiale

Cette calculatrice vous aide à effectuer une division longue entre deux polynômes donnés. Pour ce faire, vous devez fournir deux expressions polynomiales valides. Ces polynômes peuvent être déjà simplifiés ou non, et la calculatrice les simplifiera si nécessaire.

Lorsque diviser des polynômes vous devez fournir deux polynômes, celui que vous allez diviser, qui est appelé le dividende, et l'autre, le diviseur.

Une fois que vous aurez fourni deux polynômes l'étape suivante consiste à cliquer sur le bouton "Calculer", qui affichera tous les calculs nécessaires à la division longue souhaitée entre les polynômes fournis.

Le processus de réalisation d'une division de polynômes à l'aide de l'outil Méthode De Division Longue est une méthode relativement simple, mais qui nécessite une approche très organisée, afin de ne pas se perdre. En général, il est préférable d'utiliser une approche tabulaire pour montrer les étapes correspondantes.

Une approche plus simple est utilisée avec Division synthétique mais cela ne s'applique que lorsque le diviseur est de degré un, donc sa portée est plus limitée

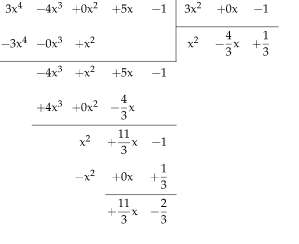
Qu'est-ce qu'un polynôme ?

Un polynôme est un type d'expression simple qui combine avec des sommes et des soustractions les puissances entières d'une certaine variable x (ou quel que soit le nom de la variable choisie), éventuellement multipliées par des constantes.

Par exemple, l'expression \(p(x) = 2x^2 + x + 1\) est une combinaison des termes \(2x^2\), \(x\) et \(1\) avec des additions de puissances de x (remarquez que 1 est une puissance de x, comme \(x^0 = 1\).

En revanche, \(f(x) = 2x^2 + \sin(x) + 1\) n'est pas un polynôme, car le terme \(\sin(x)\) n'est pas une puissance de x.

Opérations polynomiales

Les polynômes, tout comme les nombres, peuvent être manipulés avec addition, soustraction, multiplication et division de polynômes . Les additions et les soustractions sont simples à réaliser, de manière très intuitive. Par exemple, si vous avez deux polynômes, \(p(x) = 2x+1\) et \(q(x) = x^3 + 2x+ 3\), l'addition du polynôme est réalisée en ajoutant littéralement les termes comme

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

Pour les soustractions, vous soustrayez également les termes correspondants du polynôme qui est soustrait. Par exemple, si vous avez deux polynômes, \(p(x) = 2x+1\) et \(q(x) = x^3 + 2x+ 3\), alors, la soustraction se fait comme suit

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

La multiplication est plus compliquée, car vous devez effectuer une multiplication croisée des termes en utilisant la propriété distributive :

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

La division est légèrement plus compliquée, car elle implique l'idée qu'un polynôme ne peut pas diviser exactement un autre polynôme. Mathématiquement, lorsqu'on a deux polynômes \(p(x)\) et \(s(x)\), et qu'on veut diviser \(p(x)\) par \(s(x)\), on cherche un quotient \(q(x)\) et un reste \(r(x)\) (tous deux polynomiaux), qui ont la propriété que \(p(x)= q(x)\cdot s(x) + r(x)\), avec la condition que le.. degré du polynôme \(r(x)\) est inférieur au degré de \(s(x)\). On appelle généralement cela le Décomposition D'Euclide .

La méthode de la division longue

Ainsi, la méthode de la division longue est une façon systématique de commencer avec deux polynômes que nous voulons diviser \(p(x)\) et \(s(x)\), donc nous trouvons un quotient \(q(x)\) et un reste \(r(x)\) de telle sorte que..

\[p(x)= q(x)\cdot s(x) + r(x)\]

Cet algorithme est extrêmement utile, et bien que le problème soit simple en apparence, il n'est pas difficile de s'y perdre si l'on n'utilise pas une approche systématique, qui est garantie d'arriver au quotient et au reste requis.

Quelles sont les étapes pour effectuer une division longue ?

• Étape 1: Identifiez les deux polynômes p(x) et s(x) que vous voulez diviser et identifiez p(x) comme dividende et s(x) comme diviseur
• Étape 2: Vérifiez le degré du dividende p(x) par rapport au degré de s(x). Si le degré de s(x) est plus grand que le degré de p(x), nous avons que le reste est le dividende p(x) lui-même, et le quotient est zéro : q(x) = 0, et vous avez terminé
• Étape 3: Dans ce cas, nous supposons que le degré du dividende p(x) est supérieur ou égal au degré de la division s(x), sinon nous nous serions arrêtés à l'étape 2
• Étape 4: Nous devons mener un processus itératif pour trouver un reste temporaire, jusqu'à ce que nous arrivions à un reste dont le degré est inférieur au degré de s(x)
• Étape 5 : Le reste temporaire ou provisoire est mis à jour à chaque fois en trouvant d'abord le rapport entre le terme le plus élevé du reste temporaire actuel et le diviseur s(x). Ce rapport (qui est un terme de puissance) est multiplié puis s(x), et le résultat de cette multiplication est soustrait du reste temporaire actuel, ce qui conduit à un reste actualisé
• Étape 6 : Ce processus se poursuit jusqu'à ce que le reste ait un degré inférieur à celui de s(x). À chaque étape de l'itération, le degré du reste temporaire est réduit d'au moins 1, ce qui garantit la fin du processus

En fin de compte, le processus de diviser deux polynômes est réduite à calculer des multiplications sont des sommes de polynômes, ce qui est à peu près ce qui se passe avec les nombres. La méthode de division longue pour les polynômes est l'extension de la façon dont nous divisons les nombres aux polynômes.

Quel est le lien entre la division longue et la recherche des racines d'une équation polynomiale ?

Supposons que p(x) soit le dividende que vous voulez diviser et que s(x) soit le diviseur. Selon la méthode de la division longue, vous serez en mesure de trouver un quotient q(x) et un reste r(x) de sorte que :

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

Mais parfois, il arrive que le reste soit r(x) = 0, et dans ce cas on dit que s(x) divise p(x) (ou qu'il divise exactement p(x)). Donc, lorsque r(x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

Cela indique que pour trouver les racines de p(x) = 0, nous pouvons résoudre q(x) = 0 et s(x) = 0, séparément, qui sont des équations plus simples à résoudre.

Avantages de cette calculatrice de division longue

Comme je l'ai déjà mentionné, la division longue n'est pas trop difficile, mais elle nécessite une approche systématique. Un grand avantage de l'utilisation d'un calculatrice de division comme celui-ci, c'est que vous aurez toutes les étapes du processus montrées

Il n'est peut-être pas essentiel de savoir comment effectuer les étapes soi-même, mais cette calculatrice vous permet de voir comment procéder, chaque étape étant expliquée, ce qui élimine le mystère de l'obtention du reste et du quotient à partir, par exemple, d'une calculatrice numérique, qui vous donnera la réponse sans montrer les étapes.

Une calculatrice de division longue avec des étapes montrant tout le travail vous permet d'avoir une idée claire de ce qui se passe dans le calcul.

Exemple : calcul de la division de polynômes

Calculez la division des polynômes suivants : \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) et \(s(x) = x+3\).

Solution: On a fourni le polynôme suivant : \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\), qui doit être divisé par le polynôme \(\displaystyle s(x) = x+3\).

Observez que le degré du dividende est \(\displaystyle deg(p) = 3\), alors que le degré du diviseur est \(\displaystyle deg(s)) = 1\).

Étape 1: Le terme principal du dividende \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) est \(\displaystyle \frac{1}{3}x^3\), tandis que le terme principal du diviseur \(\displaystyle s(x) = x+3\) est égal à \(\displaystyle x\).

Ainsi donc, le terme que nous devons multiplier \(x\) pour obtenir le terme de tête du dividende est \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\), nous ajoutons donc ce terme au quotient. De même, nous le multiplions par le diviseur pour obtenir \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\), que nous devons soustraire au dividende :

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Étape 2: Dans ce cas, le terme principal du reste actuel \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) est <, et nous savons que le terme principal du diviseur est \(\displaystyle x\).

Ainsi donc, le terme que nous devons multiplier \(x\) pour arriver au terme de tête du de reste actuel est \(\displaystyle \frac{ -1x^2}{ x} = -x\), donc nous ajoutons ce terme au quotient. De même, nous le multiplions par le diviseur pour obtenir \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\), que nous devons soustraire au reste actuel :

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Étape 3: Dans ce cas, le terme principal du reste actuel \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) est <, et nous savons que le terme principal du diviseur est \(\displaystyle x\).

Ainsi donc, le terme que nous devons multiplier \(x\) pour arriver au terme de tête du de reste actuel est \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\), donc nous ajoutons ce terme au quotient. De même, nous le multiplions par le diviseur pour obtenir \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\), que nous devons soustraire au reste actuel :

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

qui conclut ce calcul, puisque le degré du reste actuel \(r(x) = -\frac{163}{12}\) est inférieur au degré du diviseur \(s(x) = x+3\).

Conclusion : Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that