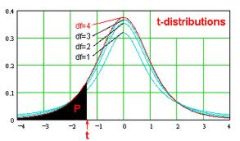
Valeurs t critiques
Instructions : Calculez les valeurs critiques de t pour la distribution t en utilisant le formulaire ci-dessous. Veuillez indiquer le niveau de signification \(\alpha\), le nombre de degrés de liberté et le type de queue (gauche, droite ou double)
Comment utiliser la calculatrice des valeurs t critiques ?
Plus d'informations sur Valeurs critiques pour la distribution t : Tout d'abord, les valeurs critiques sont des points situés dans la (les) queue(s) d'une distribution spécifique, avec la propriété que l'aire sous la courbe pour ces points critiques dans les queues est égale à la valeur donnée de \(\alpha\)
Dans ce cas, la distribution est la distribution T-Student. En termes généraux, pour un cas bilatéral, les valeurs critiques correspondent à deux points à gauche et à droite du centre de la distribution, qui ont la propriété que la somme de l'aire sous la courbe pour la queue gauche (à partir du point critique gauche) et l'aire sous la courbe pour la queue droite est égale au niveau de signification donné \(\alpha\).
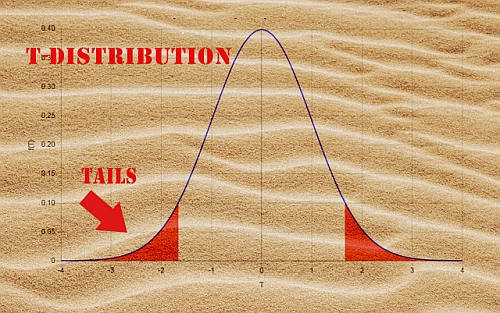
Valeurs t critiques
Dans le cas d'une queue gauche, la valeur critique correspond au point situé à gauche du centre de la distribution, avec la propriété que l'aire sous la courbe pour la queue gauche (du point critique à la gauche) est égale au niveau de signification donné \(\alpha\).
Dans le cas d'une queue droite, la valeur critique correspond au point situé à droite du centre de la distribution, avec la propriété que l'aire sous la courbe pour la queue droite (du point critique à la droite) est égale au niveau de signification donné \(\alpha\).
Quelles sont les principales propriétés de la distribution t ?
Les principales propriétés de la distribution T et de ses points critiques sont les suivantes :
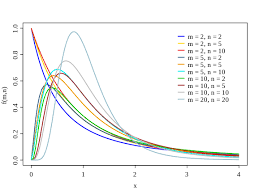
- La distribution t est une distribution symétrique et continue, qui est déterminée par le nombre de degrés de liberté (df)
- La distribution t converge (au sens distributionnel) vers la distribution normale standard (distribution Z) lorsque les degrés de liberté (df) convergent vers l'infini
- La distribution t est utilisée pour divers tests t, lorsque l'écart-type de la population n'est pas connu
- La distribution t étant symétrique, les points critiques pour le cas bilatéral sont symétriques par rapport au centre de la distribution
- De plus, comme la distribution t est symétrique, la recherche des valeurs critiques pour un test bilatéral avec une signification de \(\alpha\) est la même que la recherche des valeurs critiques unilatérales pour une signification de \(\alpha\)/2
La distribution t est la distribution sous-jacente utilisée pour la distribution très couramment utilisée dans les applications statistiques Test T pour les échantillons appariés et test t pour deux échantillons indépendants . Ces tests sont essentiels pour évaluer la signification statistique des différences, pour les données appariées et non appariées.
Ai-je besoin d'un tableau des valeurs critiques t ?
Techniquement, vous pouvez utiliser un tableau de valeurs critiques t, que vous trouverez à la fin de votre livre Stats 101, mais en utilisant ce tableau, vous obtiendrez une valeur critique calculatrice de la valeur t critique éliminera ce besoin. Lorsque vous travaillez avec des tableaux statistiques, vous devez trouver le bon tableau et la bonne position pour le nombre de degrés de liberté et le niveau alpha correspondants.
Dans le cas de notre calculatrice, vous indiquez les degrés de liberté et le niveau alpha, puis vous appuyez sur un bouton. Vous obtenez alors la valeur t-critique demandée ainsi que la valeur graphique de distribution t montrant la (les) queue(s) correcte(s) associée(s) à la (aux) valeur(s) critique(s).
Exemple : Exemple de calcul de la valeur t critique
Quelle est la valeur t-critique pour alpha = 0,01, pour un test bilatéral, avec une taille d'échantillon de n = 31 ?
Solution : Tout d'abord, le nombre de degrés de liberté est df = n - 1 = 31 - 1 = 30. Par conséquent, pour un test bilatéral, nous devons trouver la valeur de la distribution t avec 30 degrés de liberté qui a une probabilité de 0,01/2 = 0,005 sur la queue droite.
Par conséquent, la valeur t critique est \(t_c = 2.750\). Comme il s'agit d'un test bilatéral, les valeurs critiques sont \(t_c = \pm 2.750\).
Graphiquement :
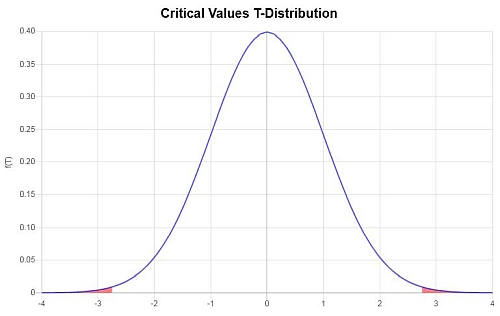
De plus, la région de rejet associée est \(R = \{t: |t| > 2.750\}\)
Autres calculateurs de valeurs critiques
Celle-ci permet de trouver les valeurs t. Nous disposons de nombreux autres calculateurs de valeurs critiques, tels que le calculateur de valeurs critiques z , Calculateur de valeurs critiques F et le Calculatrice de la valeur critique du Khi-deux .
L'utilisation des valeurs critiques est l'une des approches les plus courantes pour tester les hypothèses statistiques, en comparant les valeurs obtenues par une méthode d'analyse statistique calculateur de valeur de test avec les valeurs critiques correspondantes, car les valeurs critiques sont en effet directement utilisées pour construire les régions de rejet.