En savoir plus sur le graphique de probabilité normale

Un graphique de probabilité normale est un graphique généralement utilisé pour évaluer la normalité de la distribution à laquelle appartiennent les données d'échantillon transmises.

Il existe différents types de courbes de normalité (PP, QQ et autres), mais elles fonctionnent toutes selon le même principe : les quantiles théoriques d'une distribution normale standard sont représentés graphiquement par rapport aux quantiles observés.

Par conséquent, si les données de l’échantillon proviennent d’un population distribuée de manière normale , alors le tracé de probabilité normal devrait ressembler à un 45 ^o Une ligne, avec des variations aléatoires. Si ce n'est pas le cas et que le tracé de la courbe de probabilité normale s'en écarte significativement/systématiquement, on peut alors suspecter une distribution anormale.

Comment calculer un tracé de probabilité normale ?

Il y a plusieurs étapes concrètes que vous devez suivre, dans un ordre spécifique, pour construire un tracé de probabilité normale

1. Dans ce cas concret, les données sont classées par ordre croissant, et nous appelons ces données \(X_1, X_2, ...., X_i , ...., X_n\).
2. Pour chaque \(X_i\) dans cette séquence de données ordonnées, nous calculons les fréquences théoriques \(f_i\), qui sont approximées à l'aide de la formule suivante :
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. Nous calculons ensuite également \(z_i\), qui correspond au score z associé comme
\[ z_i = \Phi^{-1}(f_i)\]
4. Ensuite, le tracé de probabilité normale est obtenu en traçant les valeurs X ordonnées (vos données d'échantillon) sur l'axe horizontal et les valeurs \(z_i\) correspondantes sur votre axe vertical.

Diagramme de probabilité normale excel

Vous pouvez tracer un graphique de probabilité normale dans Excel, mais cela prend un certain temps. Yo

Calculatrices pour la distribution normale et autres

D'autres créateurs de cartes que vous pouvez utiliser sont nos graphique de distribution normale , Créateur de diagrammes de dispersion ou notre Créateur de diagramme de Pareto .

Exemple : calcul d'un tracé de probabilité normale

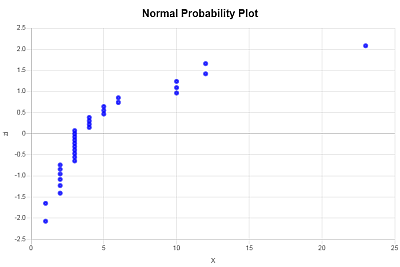
Question :Vous disposez des exemples de données suivants : 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 et 23. Construisez un diagramme de probabilité normale.

Solution :

Nous devons construire un diagramme de probabilité normale. Voici les exemples de données fournis :

Observation:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

Les fréquences théoriques \(f_i\) doivent être calculées ainsi que les z-scores associés \(z_i\), pour \(i = 1, 2, ..., 33\) :

Notez que les fréquences théoriques \(f_i\) sont approximées à l'aide de la formule suivante :

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

Où \(i\) correspond à la position dans l'ensemble de données ordonné, et \(z_i\) au score z associé correspondant. Ce résultat est calculé comme suit :

\[ z_i = \Phi^{-1}(f_i)\]

Le tableau suivant est obtenu

Position (i)	X (Ordre Croissant)	f je	z je
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

Le diagramme de probabilité normale est obtenu en portant les valeurs X (données de l'échantillon) sur l'axe horizontal et les valeurs \(z_i\) correspondantes sur l'axe vertical. Le diagramme de normalité suivant est obtenu :