Más sobre la gráfica de funciones inversas

Esta calculadora le ayudará a encontrar la gráfica de la función inversa que proporcione, siempre que la función tenga una inversa, lo que no siempre es el caso.

Puede proporcionar una función en el formato 'y = 2x - 1', o simplemente dar una expresión como 'f(x) = (x-1)/(x-3)' o simplemente '(x-1)/( x-3)' para especificar la función.

Una vez que haya proporcionado una función válida, puede hacer clic en el botón "Calcular" y se le proporcionarán todos los pasos de la cálculo de la función inversa , y si existe la inversa, entonces se mostrará una gráfica con la función y la inversa.

Observe que para que la función dada tenga una función inversa, la función debe ser uno a uno, lo que significa que cada valor en el rango de la función tiene como máximo una preimagen en el dominio de la función. y exactamente una preimagen en la que restringimos el alcance efectivo.

Cómo saber si una función es invertible

Antes de obtener la gráfica de la inversa de una función determinada, necesitas saber si la función tiene alguna inversa. El criterio principal para tener una inversa es que sea uno a uno, lo que significa que un valor en el rango no puede tener dos valores asociados (preimágenes).

Posiblemente los estudiantes prefieran no usar términos técnicos como "imágenes" y "preimágenes", y aunque esos son conceptos centrales en la teoría de funciones, en este caso podemos usar una prueba gráfica simple para evaluar si una función es uno a uno. uno y, por lo tanto, si puedes encontrar y graficar su inversa.

Prueba de línea horizontal

La prueba de la línea horizontal indica que para que una función sea uno a uno, cualquier línea horizontal que construya cruzará la gráfica de la función como máximo una vez. Si puedes encontrar una línea horizontal que cruce la gráfica de la función dada más de una vez, entonces la función NO ES uno a uno.

Por ejemplo, la función que se muestra a continuación es uno a uno, porque no importa qué línea horizontal le arrojemos, cruzará la gráfica de la función exactamente una vez:

Pero entonces, el siguiente ejemplo muestra una función que no es uno a uno, porque vemos una línea horizontal que cruza la línea de la función 2 veces (más de una vez):

Pasos para encontrar la gráfica inversa

• Paso 1: Hay dos métodos comunes: uno es el método gráfico y el otro es el método analítico
• Paso 2: Para el método gráfico, primero debe aplicar la prueba de la línea horizontal y asegurarse de que la pase, de modo que sea uno a uno y exista lo inverso
• Paso 3: Luego, dibujas la recta y = x en la gráfica (una recta que tiene un ángulo de 45 ^o grados con respecto al eje x
• Etapa 4: Después de eso, simplemente usa la línea y = x como un 'espejo' y refleja los puntos del gráfico original con respecto al 'espejo'. La gráfica obtenida con este proceso de duplicación es la gráfica de la inversa
• Paso 5: Para el método analítico, primero es necesario algebraicamente encontrar la inversa : Comienzas con y = f(x) y luego resuelves para y.
• Paso 6: Si solo hay una solución, entonces existe la inversa y se escribe x = g(y). Al ajustar los nombres de las variables, se define formalmente la función inversa \(f^{-1}\) en términos de g
• Paso 7: Finalmente, graficas el inverso que encontraste \(f^{-1}\) como lo harías graficar una función normalmente

Cuando necesitas encontrar la gráfica de una inversa, tanto el método gráfico como el analítico están bien, solo el método analítico tiene una ventaja, que es que calculas la función inversa a lo largo del proceso, por lo que terminas teniendo una expresión matemática de la misma. no sólo su gráfico.

¿por qué graficarías la inversa?

Hay tantas razones por las que harías eso. Primero, la función inversa en sí misma es un actor muy importante en la teoría de funciones, ya que una función muestra cómo pasar de x a ay, por lo que es natural querer saber cuál es el mecanismo para pasar de y a x, y eso es precisamente lo que te proporciona la función inversa.

Entonces, uno podría pensar en una función como un mapa unidireccional desde un punto "X" a un punto "Y", y calcular la función inversa es como definir explícitamente un mapa para ir de "Y" a "X".

Y luego la gráfica de la inversa te dará mucha información sobre esa función inversa: si sube, cómo se comporta.

¿cómo me ayuda esta calculadora de función gráfica inversa?

Primero, esta calculadora analizará la función para ver si es invertible utilizando el método analítico y, si es posible encontrar dicha inversa, la graficará por usted.

Encontrar la inversa implica resolviendo una ecuación , lo cual no es una tarea fácil a menos que se trate de Ecuaciones lineales o ecuaciones polinómicas , pero aparte de eso, el proceso puede ser muy complejo o incluso imposible.

Otras calculadoras pueden realizar un proceso similar, pero una de las ventajas de esta calculadora es que proporciona todos los pasos del proceso, con una explicación detallada, cuando sea posible.

Ejemplo: encontrar la gráfica de la inversa

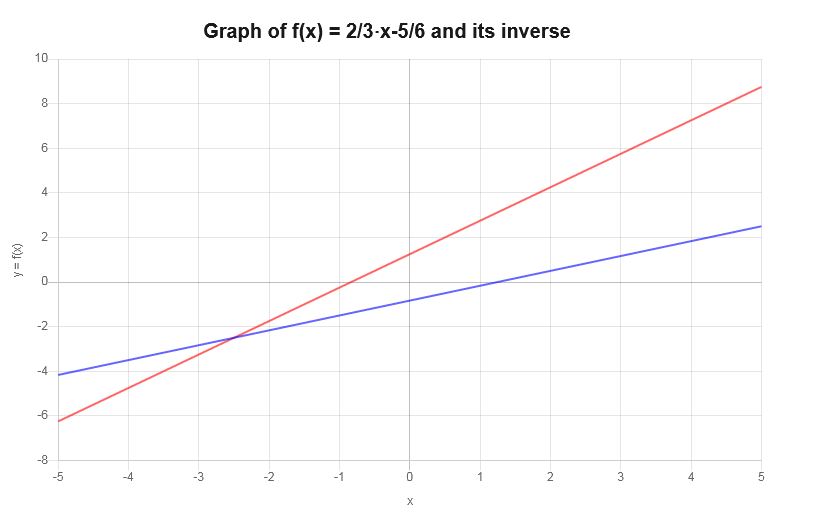
Grafique la inversa de: \( y = \frac{2}{3} x - \frac{5}{6}\)

Solución:

Se nos ha proporcionado la siguiente función:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Luego, para encontrar la inversa de la función dada, necesitamos resolver \(x\) y determinar si hay una solución o no. La ecuación inicial es

\[y=\frac{2}{3}x-\frac{5}{6}\]

Paso 0: En este caso, primero necesitamos simplificar la ecuación lineal dada y, para hacerlo, llevamos a cabo los siguientes pasos de simplificación:

Resolver la ecuación lineal

Poniendo \(x\) en el lado izquierdo y \(y\) y la constante en el lado derecho obtenemos

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Ahora, resolviendo \(x\), al dividir ambos lados de la ecuación entre \(-\frac{2}{3}\), se obtiene lo siguiente

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

y simplificando obtenemos finalmente lo siguiente

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Por lo tanto, resolver \(y\) para una ecuación lineal dada conduce a \(x = \frac{3}{2}y+\frac{5}{4}\).

Por tanto, y como al resolver para \(x\) encontramos solución y es sólo una solución, hemos encontrado la inversa.

La función inversa encontrada

Con base en el trabajo mostrado arriba, se puede concluir que la función inversa es:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

La función inversa se puede mostrar gráficamente de la siguiente manera:

Ejemplo: más gráficas inversas

¿Puedes encontrar la gráfica inversa de: \(y = x^2\)?

Solución: No, no podemos encontrar la gráfica inversa de \(y = x^2\), ya que esta función no pasa la prueba de la línea horizontal. Otra forma de verlo es que al resolver para \(x\) obtenemos \(x = \pm \sqrt y\), y como encontramos dos soluciones, entonces no hay inversa y, en consecuencia, no hay gráfica inversa.

Más calculadoras de funciones

Las funciones y cualquier tipo de operación de funciones son verdaderamente el centro del Álgebra y el Cálculo. Un bien Calculadora de funciones le hará la vida más fácil en términos de reducir una función a su expresión más simple.

Entonces tendrás un buen herramienta gráfica de funciones para echar un vistazo rápido a las propiedades gráficas de una función. Ver la gráfica de una función puede decirte mucho sobre su comportamiento, incluso antes de mirar su expresión algebraica.

Luego tienes operaciones más avanzadas como encontrar la derivada, para lo cual esto Calculadora de diferenciación Te resultará útil, ya que te muestra todos los pasos del proceso. Como era de esperar, la derivada de la función inversa tiene una asociación interesante con la derivada de la función original.