Acerca de este graficador de desigualdades

Esta calculadora te ayudará a encontrar la solución y la gráfica de cualquier desigualdad general, mostrando todos los pasos. Debe proporcionar una desigualdad válida de una variable (x) escribiéndola en el cuadro correspondiente.

Por ejemplo, puedes proporcionar una desigualdad lineal simple como '3x - 1 < 1/3', o algo como '2x-x^2 <= 3/4', que corresponde a una desigualdad cuadrática.

Una vez que haya proporcionado la desigualdad que desea graficar, continúe y haga clic en el botón "Resolver", para que se le presenten las soluciones, con todos los pasos, en caso de que fuera posible encontrar soluciones.

Resolver ecuaciones generales y las desigualdades generales es en general una tarea difícil, excepto para un conjunto específico de estructuras que son susceptibles de un tratamiento sistemático.

Algunos de los pocos tipos que permiten una solución exacta son desigualdades lineales y desigualdades polinomiales .

Un tipo importante de desigualdad que te gustaría resolver es el caso de desigualdades racionales, en las que puedes identificar un cociente de polinomios. Esas desigualdades son interesantes porque tienen divisiones potenciales entre cero que es necesario abordar. La idea de una desigualdad racional se puede extender fácilmente al cociente de funciones en general, no necesariamente a polinomios

Cómo graficar una desigualdad

La respuesta más simple es: para graficar una desigualdad, necesitas saber cómo resolverla. La solución gráfica de una desigualdad suele representarse como un intervalo o varios intervalos unidos en el eje x.

Entonces, dicho esto, para graficar una desigualdad se comenzará resolviéndola primero, lo que implica encontrar un conjunto de valores en la recta real que satisfagan la desigualdad proporcionada.

Potencialmente, puedes presentar la gráfica como un intervalo independiente, o puedes trazar las soluciones de la desigualdad junto con la gráfica de la expresión subyacente a la desigualdad: recordemos que para Resolver desigualdades , pasas todos los términos a un lado (lo que te da la expresión subyacente) y resuelves una ecuación auxiliar

Pasos para resolver y representar gráficamente desigualdades

• Paso 1: Pase todos los términos a un lado, de modo que tenga una expresión en un lado y cero en el otro lado
• Paso 2: A partir de la desigualdad (una vez que todo está en un lado y cero en el otro), construye una ecuación auxiliar
• Paso 3: Resuelva esta ecuación con un método que sea adecuado para su estructura (diferentes tipos de ecuaciones requerirán técnicas y enfoques específicos)
• Etapa 4: Con base en las soluciones REALES de las ecuaciones auxiliares (reales en contraposición a soluciones complejas), usted construye sus puntos críticos y los ordena en orden ascendente
• Paso 5: También es necesario buscar puntos donde la expresión no esté definida. Un caso notable de esto ocurre con las desigualdades racionales, en las que tienes un denominador que es un polinomio, por lo que la expresión no estará definida en los ceros del denominador. Entonces agregas ceros del denominador a la lista de puntos críticos
• Paso 6: Con sus puntos críticos, construye intervalos usando puntos críticos consecutivos (usando -∞ y ∞ como puntos críticos iniciales y finales)
• Paso 7: Para cada intervalo, analiza el signo de la expresión y ve si es compatible con el signo de la desigualdad. Si es así, entonces el intervalo será parte de la solución general de la desigualdad

Usar puntos críticos para el análisis es de suma importancia, porque de esa manera estás seguro de que la expresión no cambia de signo dentro de cada intervalo, por lo que el problema se reduce a evaluar si la desigualdad se resuelve para cada uno de esos intervalos críticos.

Para hacerlo un poco más tangible, tienes cierta desigualdad dada y luego pasas todo a un lado, por lo que tienes algo de la forma \(f(x) \le 0\). Por ejemplo, esto podría ser algo así como \(x^2 - x + 1 \le 0\).

Entonces tomas \(f(x) \le 0\) y encuentras la ecuación auxiliar \(f(x) = 0\). Tomas la expresión \(f(x)\) y encuentras que sus ceros son los puntos críticos. Pero no sólo haces eso, sino que también ves si \(f(x)\) no está definido en algún lugar (divisiones por cero, etc.). Quizás esté definido en todas partes, como en el caso \(x^2 - x + 1\), pero si encuentra puntos donde la expresión no está definida, la agrega a la lista de puntos críticos.

Luego construyes intervalos basados en puntos críticos consecutivos. Para el \(f(x) \le 0\), tomarás como parte de las soluciones aquellos intervalos donde el valor de la expresión sea negativo. Si la desigualdad original hubiera sido \(f(x) \ge 0\) tomarás como parte de las soluciones aquellos intervalos donde el valor de la expresión sea positivo

Cómo funciona este gráfico de desigualdad

Nuestro graficador de desigualdades en línea se encargará de uno de los procesos más engorrosos del álgebra básica, que consiste en encontrar las soluciones de una desigualdad y graficarlas. Una gran ventaja de nuestra calculadora es que mostrará todos los pasos, cuando sea posible.

Primero, el graficador resolverá la desigualdad resolviendo primero una ecuación auxiliar adecuada. Este proceso requiere detectar estructuras conocidas específicas, ya que es probable que todas las estructuras requieran enfoques diferentes. Por ejemplo, para resolver una desigualdad racional (que involucra el cociente de dos polinomios) como por ejemplo

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

necesitarás un enfoque diferente al utilizado para resolver una desigualdad cuadrática como \(x^2 + 3x < 1\), por ejemplo, y esta calculadora tendrá en cuenta todos esos detalles

Si no se detecta ninguna estructura tradicional o comúnmente conocida, se utilizarán diferentes sustituciones comúnmente utilizadas, como por ejemplo \(u = \sqrt x\) o \(u = \sin x\). Si nada funciona, la calculadora intentará encontrar soluciones mediante inspección y numéricamente, para tener al menos una idea de las soluciones.

¿cómo se presenta una gráfica de desigualdad?

Como mencionamos anteriormente, en realidad no está escrito en piedra, pero la forma más común es graficar la expresión subyacente de la desigualdad y resaltar los valores de x que satisfacen la desigualdad. Este es posiblemente el mejor formato gráfico para esto, y es el que utiliza este graficador.

También puedes dibujar un objeto de intervalo independiente, pero posiblemente sea menos revelador, ya que pierde la perspectiva de lo que realmente está sucediendo con la desigualdad misma.

Ejemplo: graficar desigualdades

Grafica la siguiente desigualdad: \(\frac{1}{x}+x > 1\)

Solución: Se nos da la siguiente desigualdad que debe resolverse:

\[\frac{1}{x}+x > 1\]

Necesitamos poner todos los términos de la desigualdad a un lado:

\[x+\frac{1}{x}-1>0\]

Resolver ecuaciones auxiliares

De la desigualdad anterior, obtenemos la ecuación asociada que debe resolverse primero:

\[x+\frac{1}{x}-1=0\]

Análisis de puntos críticos

Necesitamos organizar los puntos críticos encontrados (a partir de las raíces reales del numerador y denominador) en orden ascendente, definir intervalos con todos los puntos críticos consecutivos y evaluar el signo del tamaño izquierdo de la desigualdad en cada uno de esos intervalos. .

El único punto crítico que se encontró es \(0\).

En base a esto, debemos analizar los siguientes intervalos:

• Para el intervalo \(\left(-\infty, 0\right)\): El numerador es positivo y el denominador es negativo, entonces el lado izquierdo es negativo, lo que implica que \(\left(-\infty, 0\right)\) no es parte de la solución.

• Para el intervalo \(\left(0, \infty\right)\): El numerador es positivo y el denominador es positivo, entonces el lado izquierdo es positivo, entonces \(\left(0, \infty\right)\) es parte de la solución.

Solución a la desigualdad

Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(x > 0\).

Usando notación de intervalo, la solución se escribe como:

\[\left(0,\infty\right)\]

Con el graficador de desigualdades se obtiene lo siguiente:

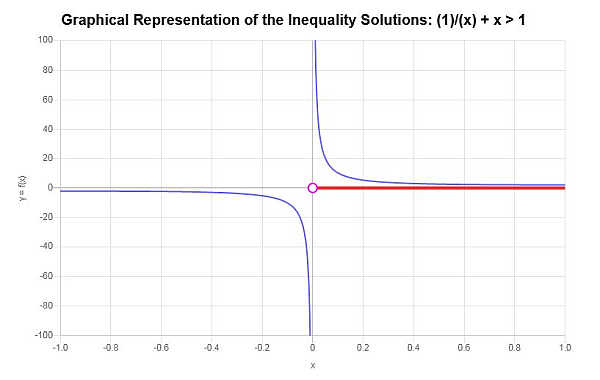
que concluye el cálculo.

Ejemplo: graficar desigualdades polinómicas

Encuentra la gráfica de la desigualdad: \(x^2 - 2x \ge 4\)

Solución:

Necesitamos poner todos los términos de la desigualdad a un lado:

\[x^2-2x-4\ge0\]

Resolver ecuaciones auxiliares

De la desigualdad anterior, obtenemos la ecuación asociada que debe resolverse primero:

\[x^2-2x-4=0\]

Usando la fórmula cuadrática

Para una ecuación cuadrática de la forma \(a x^2 + bx + c = 0\), las raíces se calculan usando la siguiente fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

En este caso, tenemos que la ecuación que necesitamos resolver es \(\displaystyle x^2-2x-4 = 0\), lo que implica que los coeficientes correspondientes son:

\[a = 1\] \[b = -2\] \[c = -4\]

Primero, calcularemos el discriminante para evaluar la naturaleza de las raíces. La discriminación se calcula como:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

Como en este caso obtenemos que el discriminante es \(\Delta = \displaystyle 20 > 0\), que es positivo, sabemos que la ecuación tiene dos raíces reales diferentes.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

entonces, encontramos que:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

En este caso, la ecuación cuadrática \( \displaystyle x^2-2x-4 = 0 \), tiene dos raíces reales, entonces:

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

entonces el polinomio original se factoriza como \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \), lo que completa la factorización.

Análisis de puntos críticos

La lista de puntos críticos encontrados organizados en orden ascendente es: \(-\sqrt{5}+1\), \(\sqrt{5}+1\).

En base a esto, debemos analizar los siguientes intervalos:

• Para el intervalo \(\left(-\infty, -\sqrt{5}+1\right)\): El lado izquierdo es positivo, entonces \(\left(-\infty, -\sqrt{5}+1\right)\) es parte de la solución.

• Para el intervalo \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\): El lado izquierdo es negativo, por lo que \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) no es parte de la solución.

• Para el intervalo \(\left(\sqrt{5}+1, \infty\right)\): El lado izquierdo es positivo, lo que implica que \(\left(\sqrt{5}+1, \infty\right)\) es parte de la solución.

Solución a la desigualdad

Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(x \le -\sqrt{5}+1\) o \(x \ge \sqrt{5}+1\).

Usando notación de intervalo, la solución se escribe como:

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

Gráficamente:

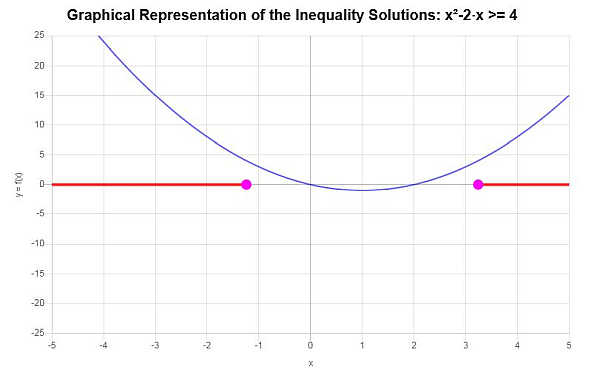
que concluye el cálculo.

Más calculadoras de álgebra

A medida que avanza en su aprendizaje de Álgebra y Cálculo, probablemente se habrá dado cuenta poco a poco de que Resolver ecuaciones jugar un papel crucial. Y a medida que aprendes más, te das cuenta de que a veces tenemos menos información y terminamos enfrentando el problema de Resolver desigualdades .

En esencia, resolver desigualdades no es más difícil que resolver ecuaciones, sólo requiere algunos pasos más organizados. El principal problema es que realmente no podemos resolver la mayoría de las ecuaciones, al menos exactamente.

E incluso si resolvemos ecuaciones numéricamente, todavía no tenemos buenos métodos para asegurarnos de haber encontrado TODAS las soluciones de TODAS las ecuaciones posibles. Algunas ecuaciones notables que se pueden resolver y aparecen en aplicaciones todo el tiempo son las ecuaciones polinómicas , que puedes resolver utilizando principalmente métodos estándar (pero solo para polinomios de menor grado)

Uno de los tipos de desigualdades más frecuentes que debes resolver en tus exámenes de matemáticas son las desigualdades racionales, porque son las desigualdades simples más difíciles que puedes garantizar que se encuentre una solución (siempre que los grados involucrados sean lo suficientemente bajos, o los polinomios son bastante simples).