Derivadas trigonométricas inversas

Con esta calculadora podrás calcular derivadas de funciones trigonométricas inversas, mostrando todos los pasos del proceso.

La idea es que la función que proporcione contenga una función trigonométrica inversa, por ejemplo f(x) = x^2/arctan(x+1), solo para dar un ejemplo.

Cuando esté listo y haya terminado de escribir la función que necesita diferenciar, haga clic en el botón "Calcular" para ver todos los pasos del proceso y los cálculos.

La idea de calcular derivadas de funciones trigonométricas inversas es natural, y veremos en los siguientes párrafos que se pueden derivar directamente de la derivadas trigonométricas que tu sabes.

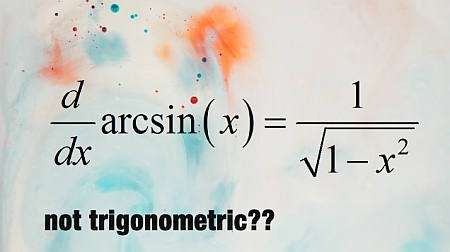
Funciones trigonométricas inversas

En términos simples, las funciones trigonométricas inversas son aquellas funciones que al evaluarlas en la función trigonométrica correspondiente conducen a la identidad. Por ejemplo, si consideramos la función \(\sin(x)\), su función inversa es \(\arcsin(x)\), y esta inversa tiene la propiedad de que

\[\sin(\arcsin(x)) = x \]

tanto como

\[\arcsin(\sin(x)) = x \]

para todo \(x\) en un cierto intervalo. Estrictamente, \(\arcsin(x)\) es la función inversa de \(\sin(x)\) desde un punto de vista algebraico. Y lo mismo ocurre con las otras funciones trigonométricas inversas y sus correspondientes funciones trigonométricas.

Cálculo de derivadas trigonométricas inversas

Entonces, si \(f\) es una función, y tiene inversa de \(f^{-1}\), entonces tenemos que

\[f^{-1}(f(x)) = x\]

para todos \(x\). Entonces, si derivamos ambos lados de la igualdad y usamos la regla de la cadena en el lado izquierdo, obtenemos

\[ \displaystyle (f^{-1})'(f(x))f'(x) = 1\] \[ \displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}\]

Ahora, si establecemos \(y = f(x)\), entonces \(x = f^{-1}(y)\), lo que lleva a

\[ \displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}\] \[ \Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}\]

¿Cómo usamos esto para funciones trigonométricas inversas? Suponga \(f(x) = \sin(x)\) y \(f^{-1}(x) = \arcsin(x)\). Entonces, según la relación general entre la derivada de una función y la derivada de su inversa, obtenemos

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}\] \[ \Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}\]

Pero un ingenioso truco geométrico nos dice que

\[\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2} \]

lo que implica que

\[ \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\]

El resto de derivadas trigonométricas inversas se obtienen con argumento similar.

¿cuáles son las 6 funciones trigonométricas inversas básicas?

• #1: \( \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}\)
• #2: \( \displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}\)
• #3: \( \displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}\)
• #4: \( \displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}\)
• #5: \( \displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\)
• #6: \( \displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}\)

Curiosamente, al calcular la derivada de las funciones trigonométricas inversas, ninguna de las derivadas trigonométricas inversas implica funciones trigonométricas o funciones trigonométricas inversas.

Aplicaciones de la derivada de funciones trigonométricas inversas

Las funciones trigonométricas y sus derivadas, así como las funciones trigonométricas inversas y sus derivadas forman parte del inventario de funciones y operaciones básicas, utilizadas como bloques de construcción para crear funciones más complicadas.

Aunque las funciones trigonométricas aparecerán con más frecuencia en las aplicaciones que las funciones trigonométricas inversas, estas últimas también tienen un lugar claro en Cálculo, especialmente cuando se diferencian y usan el método de descomposición de fracciones parciales.

Consejos y trucos

No olvides que las derivadas de funciones trigonométricas inversas pueden ser extremadamente útiles, especialmente al integrar términos que tienen un denominador cuadrático.

Además, es fácil cometer errores al calcular derivadas trigonométricas inversas por definición, definitivamente podría beneficiarse al usar un calculadora de derivadas que mostrará los pasos, o que puede utilizar para comprobar su trabajo.

Ejemplo: derivadas trigonométricas inversas

Calcular la derivada de: \(f(x) = x + \arcsin(x^2)\)

Solución: Para este primer ejemplo, analizaremos \(\displaystyle f(x)=x+\arcsin\left(x^2\right)\). Esta función involucra una función trigonométrica inversa, compuesta con otra función. Calculemos su derivada:

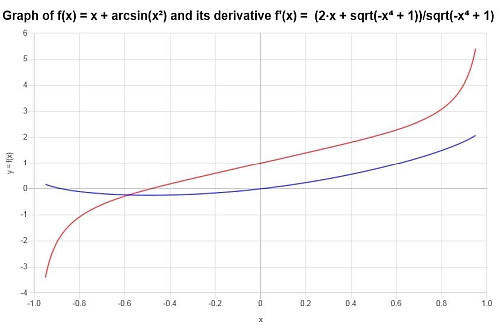
Respuesta : Podemos concluir que la derivada de la función es:

\[f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}\]

Podemos ver tanto la función como su derivada en el siguiente gráfico:

Ejemplo: más derivadas trigonométricas inversas

Considere la siguiente función: \(f(x) = \frac{\arcsin(x)}{x}\), calcule su derivada.

Solución: Ahora, para el segundo ejemplo, tenemos la función \(\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}\).

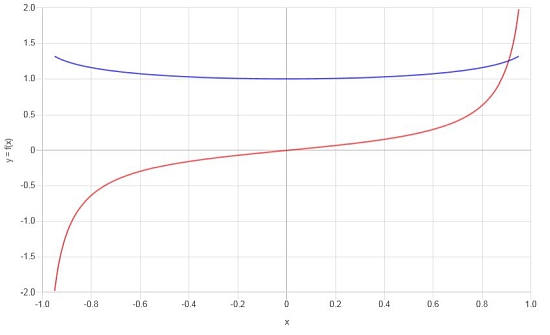
Conclusión Final : La derivada que buscamos es:

\[f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}\]

Gráficamente tenemos lo siguiente:

Ejemplo de derivadas trigonométricas inversas

Calcular la derivada de: \(f(x) = x \arctan(x+1)\)

Solución: Ahora, para este ejemplo final, trabajaremos con la función \(\displaystyle f(x)=x\arctan\left(x+1\right)\), que contiene una función inversa.

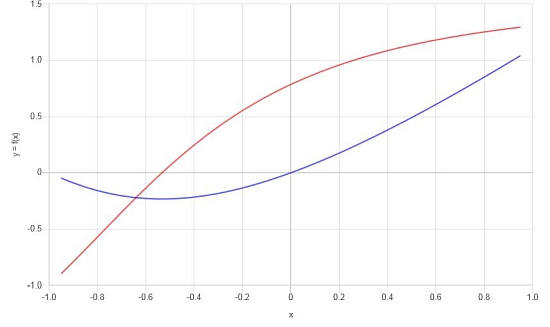
Conclusión : Después de simplificar, la derivada es:

\[f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}\]

Con base en los resultados encontrados, podemos construir el siguiente gráfico para f y f':

Otras calculadoras de cálculo

Cuando usas derivadas trigonométricas , dijimos que eran bloques de construcción cruciales para aplicar Reglas Derivadas .

Las derivadas de las funciones trigonométricas inversas se pueden derivar simplemente de la Derivados de derivadas trigonométricas básicas, y por eso también las consideramos dentro del grupo de derivadas básicas para aprender o incluso memorizar.