Mehr über diesen cos-graph-rechner

Mit diesem Rechner können Sie den Graphen für eine beliebige Kosinusfunktion erstellen, zusammen mit dem amplitude, Periode und Frequenz und zeigt alle Schritte. Sie müssen eine gültige Funktion angeben, die die Kosinusfunktion beinhaltet. Das kann etwas Triviales wie cos(x) sein oder etwas Komplizierteres wie 2*cos(1/3 x + pi) - 4/5.

Sobald Sie eine gültige Funktion mit Kosinus eingeben, klicken Sie einfach auf "Berechnen", um die Ergebnisse und alle Schritte des Prozesses angezeigt zu bekommen.

Kosinus ist eine trigonometrische Funktion die unzählige Anwendungen in Mathematik und Physik hat. Es wird auch in der Geometrie häufig verwendet, wenn lösen von Dreiecken .

Wie erstellt man ein cos-diagramm?

Das Hauptprinzip bei der grafischen Darstellung jeder Art von Funktion besteht darin, auf eine bekannte einfache Funktion zurückzugreifen, deren Graphen wir kennen, und dann den gesuchten Graphen auf der Grundlage von Übersetzungen und Skalierungen dieses einfachen Graphen zu konstruieren.

Für den Fall des cos-Graphen wissen wir, dass der einfachste Ausdruck einer Kosinusfunktion f(x) = cos(x) ist, dessen Graph unten abgebildet ist:

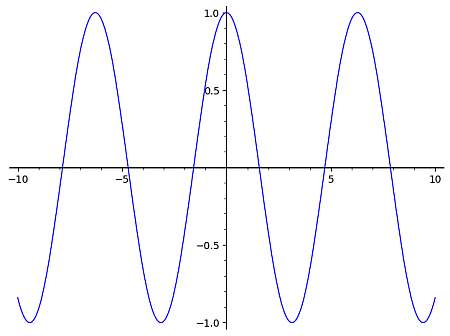
Dann können wir diesen Basisgraphen verwenden, um den Graphen von komplexeren cos-Funktionen abzuleiten, da die allgemeine Form dieselbe ist, nur dass er möglicherweise nach links oder rechts, nach unten oder oben verschoben werden kann und die Periode sich möglicherweise ebenfalls ändern kann, je nach der angegebenen Funktion.

In welchen schritten wird eine kosinusfunktion grafisch dargestellt?

• Schritt 1 : Identifizieren Sie die cos-Funktion, die Sie grafisch darstellen wollen, möglichst in der Form a*cos(bx+c)+d
• Schritt 2 : Der Wert von a entspricht der amplitude d ist die Einheit, um die der Basis-cos-Graph nach oben verschoben wird, und der Graph wird um -c/b nach rechts verschoben
• Schritt 3 : Wenn die cos-Funktion nicht die Form a*cos(bx+c)+d hat, dann erstelle eine Tabelle mit Werten für x und f(x) (wobei f(x) die gegebene cos-Funktion ist) und berechne mehrere Punkte, mit denen du manuell die Form des cos-Graphen nachzeichnen kannst

In der Tat haben nur Funktionen der Form a*cos(bx+c)+d einen eindeutigen Ausdruck für Amplitude, Periode, Frequenz und Translationen, aber sie sind nicht die einzigen Kosinusfunktionen, die man sich vorstellen kann. So ist z. B. \(f(x) = cos(x^2)\) eine cos-Funktion, aber sie hat weder Periode noch Frequenz.

Cos graph versus sine graph?

Wie ähnlich sind sich der Kosinus- und der Sinusgraph? Nun, ziemlich ähnlich. Zunächst ist zu beachten, dass es sich um den grundlegenden Kosinus- und Sinusgraphen handelt, also um sin(x) und cos(x).

Dann erhält man den cos-Graphen, indem man den Sinus-Graphen einfach um \(\pi/2\) Einheiten nach links verschiebt. Der cos-Graph und der Sinus-Graph sind also im Wesentlichen identisch, abgesehen von einer Verschiebung.

Cos-diagramm in grad

Gibt es einen Unterschied zwischen der Kosinuskurve im Bogenmaß und der Kosinuskurve in Grad? Nun, es gibt einen Unterschied in der Skalierung, da cos eine volle Periode in \(2\pi\) durchläuft, wenn er im Bogenmaß gemessen wird, und er durchläuft eine volle Periode in 360 ^o wenn sie in Grad gemessen werden. Aber in Bezug auf die Form gibt es keinen wesentlichen Unterschied.

Wie benutzt man diesen cos-graph-rechner?

Dieser cos-Rechner nimmt Ihnen das ganze Rätselraten ab, denn Sie müssen nur eine gültige cos-Funktion angeben. Je nach Art der cos-Funktion, die Sie angeben, erhalten Sie eine Periode, oder die Periode ist nicht definiert, z.B. in einem Fall wie \(f(x) = cos(x^2)\), wo wir immer noch sagen, wir haben eine cos-Funktion .

Cos-Diagramme gehören zusammen mit Sinus- und Tangens-Diagrammen zu den häufigsten trigonometrische Diagramme die Sie normalerweise antreffen werden.

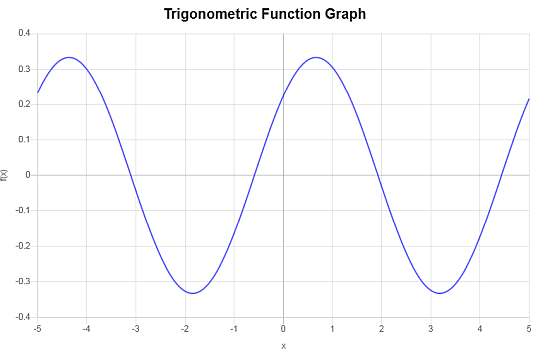
Beispiel: cos-diagramm

Berechnen Sie den Graphen von : \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\)

Lösung: Die folgende Funktion ist vorgesehen:

#XYZA

Auf der Grundlage des Arguments der übergebenen trigonometrischen Funktion werden die Frequenz und die Periode wie folgt berechnet:

#XYZA

und auch

#XYZA

Unter Berücksichtigung der angegebenen trigonometrischen Funktion \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\) ergibt sich daher Folgendes:

" Die Amplitude ist in diesem Fall \(A = 1/3\).

" Die Phasenverschiebung ist gleich \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).

" Die vertikale Verschiebung ist gleich \( 0\).

Zusammenfassend lässt sich für die gegebene trigonometrische Funktion Folgendes feststellen

• Period = \(5.0265\)
• Frequenz = \(0.1989\)
• Amplitude = \(1/3\)
• Phase Shift = \(0.6667\)
• Vertikale Verschiebung = \(\displaystyle 0\)

Nachfolgend ist das entsprechende Diagramm dargestellt

Beispiel: weitere cos-graphen

Ist die folgende Funktion periodisch? #XYZA

Lösung: Nein, das ist es nicht, wegen des Begriffs \(x^2\).

Beispiel: kosinusdiagramm

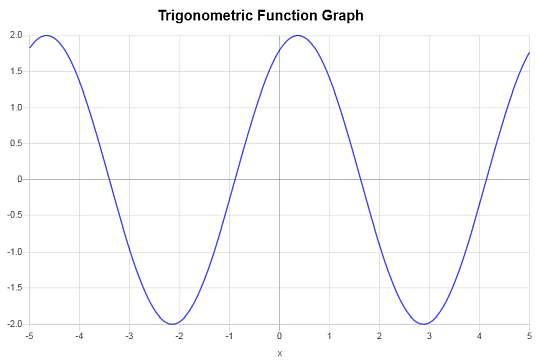
Berechnen Sie den Graphen von : \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\)

Lösung: Man beachte, dass der übergebene trigonometrische Ausdruck wie folgt vereinfacht werden kann:

die Funktion, mit der wir arbeiten werden, ist also \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).

Auf der Grundlage des Arguments der übergebenen trigonometrischen Funktion werden die Frequenz und die Periode wie folgt berechnet:

#XYZA

und auch

#XYZA

Ausgehend von der angegebenen trigonometrischen Funktion \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\) ergibt sich Folgendes:

" Die Amplitude ist in diesem Fall \(A = 2\).

" Die Phasenverschiebung ist gleich \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).

" Die vertikale Verschiebung ist gleich \( 0\).

Zusammenfassend lässt sich für die gegebene trigonometrische Funktion Folgendes feststellen

• Period = \(5.0265\)
• Frequenz = \(0.1989\)
• Amplitude = \(2\)
• Phase Shift = \(0.3667\)
• Vertikale Verschiebung = \(\displaystyle 0\)

Nachfolgend ist das entsprechende Diagramm dargestellt

Mehr geometrie-rechner

Eine der nützlichsten, die Sie finden können, ist diese perioden- und Frequenzrechner für die Sie eine beliebige trigonometrische Funktion eingeben und die Amplitude, Periode und Frequenz erhalten.

Sie können auch Folgendes verwenden sinus-Rechner mit Stufen um mit komplexeren trigonometrischen Ausdrücken zu arbeiten, die sich mit der Sinusfunktion befassen. Sinus und Kosinus sind in der Tat der Grundstein für alles, was mit Geometrie und Trigonometrie zu tun hat

Vielleicht sind Sie auch interessiert an auswerten von trigonometrischen Ausdrücken oder grafische Darstellung trigonometrischer Funktionen im Allgemeinen.