Lösen von radikalen gleichungen

Dieser Radikalgleichungslöser ermöglicht es Ihnen, die von Ihnen bereitgestellten Radikalgleichungen zu bearbeiten, indem er sie algebraisch manipuliert und Ihnen alle Schritte des Prozesses anzeigt.

Dieser Solver akzeptiert jede gültige Gleichung, die Wurzeln enthält, also etwas wirklich Einfaches wie 'sqrt(x) = 1' oder etwas, das viel schwieriger zu lösen ist wie 'sqrt(x+3) = x^2 - 1'.

Sobald Sie eine gültige Radikalgleichung eingegeben haben, sind Sie im Grunde fertig und müssen nur noch auf "Lösen" klicken, um alle Schritte des Prozesses angezeigt zu bekommen.

Die Lösung der Radikalgleichung beruht stark auf der effektiven algebraische Manipulation des Ausdrucks um den radikalen Teil grundsätzlich loszuwerden.

Was ist eine radikale gleichung?

Eine Radikalgleichung ist, sehr vereinfacht ausgedrückt, eine Art von mathematische Gleichung in denen die Unbekannte (in der Regel x) innerhalb eines Radikals steht. Zum Beispiel

\[\displaystyle \sqrt x = x^2 \]

ist wegen des Terms \( \sqrt x\) eine radikale Gleichung, aber die Gleichung

\[\displaystyle 2 x = x^2 \]

zum Beispiel ist KEINE radikalische Gleichung, weil wir nirgendwo in der Gleichung einen Insider eines Radikals finden.

Lösen von radikalen gleichungen

Das Lösen von radikalen Gleichungen ist nicht schwer, wenn Sie diese Schritte befolgen:

Manchmal ist es trotz geeigneter Gruppierung und Vereinfachung nicht möglich, die Radikale ganz zu eliminieren, oder es führt zu einer noch komplizierteren Gleichung.

Vereinfachung radikaler gleichungen

Wie bereits erwähnt, hängt die erfolgreiche Berechnung von Gleichungen mit Wurzeln stark davon ab, dass man in der Lage ist radikale vereinfachen . Aber manchmal reicht das nicht aus, da die Vereinfachung aller auftretenden Radikale sie nicht verschwinden lässt. Die gebräuchlichste Methode ist die Reduktion von Radikalen und die anschließende Anwendung des Quadrats (Potenz von 2), um das Radikal aufzuheben.

Die Quadrierung zur Beseitigung des Radikals ist jedoch ein zweischneidiges Schwert, da durch die Quadrierung jedes relevante Zeichen verschwinden könnte. Wenn wir also das Radikal "eliminieren" und Lösungen für eine Hilfsgleichung finden, MÜSSEN wir doppelt überprüfen, ob die Hilfslösungen auch Lösungen der ursprünglichen Gleichung sind. Oft sind sie das nicht.

Eine andere Möglichkeit, den Prozess der Eliminierung des Radikals zu sehen, ist die Verwendung einer geeigneten Substitution. Zum Beispiel für die Radikalgleichung:

\[\displaystyle \sqrt x = x \]

können Sie \(u = \sqrt x\) und dann \(u^2 = (\sqrt x)^2 = x\) einsetzen, so dass aus der ursprünglichen Gleichung die folgende Hilfsgleichung wird:

\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]

was eine Polynomgleichung ist, die wir lösen können. Eine Substitution führt also von einer Gleichung, von der wir nicht wissen, wie sie zu lösen ist, zu lösen einer Polynomgleichung von denen wir wissen, wer sie lösen soll.

Warum interessieren wir uns für radikale gleichungen?

Radikale Gleichungen kommen in Algebra und Kalkulation häufig vor, da sie die Grundlage für die Modellierung so vieler verschiedener Phänomene bilden.

Radikale Funktionen sind aufgrund ihrer Eigenschaften und der Art des langsamen Wachstums, wenn x sich dem Unendlichen nähert, interessant.

Beispiel: lösen von gleichungen mit radikalen

Lösen Sie die folgenden Aufgaben: \(\sqrt{x} = 2x\)

Lösung:

Wir haben die folgende Gleichung vor uns. Wir müssen diese Gleichung lösen, die nur eine Variable hat, nämlich \(x\). Das Ziel ist also, \(x\) zu lösen:

\[\sqrt{x}=x^2\]

Beachten Sie, dass der Grad des gegebenen Polynoms \(\displaystyle deg(p) = 4\) ist, sein führender Koeffizient \(\displaystyle a_{4} = -1\) und sein konstanter Koeffizient \(\displaystyle a_0 = 0\).

Versuch einer rationalen wurzel

Begründung Wurzeln Kandidaten : Da der erste Term mit einem Nicht-Null-Koeffizienten in \(p(x)\) \(x\) ist, können wir diesen Term herausrechnen und erhalten

\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]

Der Begriff in Klammern hat jedoch einen Grad, der höher als 2 ist, daher gibt es keine elementare Formel, um sie zu berücksichtigen.Wir müssen auf mögliche rationale Wurzeln testen.

Die nächste Aufgabe besteht darin, die ganzzahligen Zahlen zu finden, die den führenden Koeffizienten \(a_{3}\) und den konstanten Koeffizienten \(a_0\) teilen, die verwendet werden, um unsere Kandidaten als Nullstellen der Polynomgleichung zu konstruieren.

Dividiert man also jeden Teiler des konstanten Koeffizienten \(a_0 = 1\) durch jeden Teiler des führenden Koeffizienten \(a_{3} = -1\), so erhält man die folgende Liste von Kandidaten für Wurzeln:

\[\pm \frac{ 1}{ 1}\]

Jetzt müssen alle Kandidaten getestet werden, um festzustellen, ob sie eine Lösung sind.Das Folgende erfolgt aus dem Testen der einzelnen Kandidaten:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]

Polynomabelung : Da wir nicht genügend Wurzeln unter den rationalen Kandidaten haben, teilen wir \(\displaystyle -x^3+1\) durch das Produkt der Faktoren, die von den rationalen Wurzeln abgeleitet sind, was \(\displaystyle \left(x-1\right) \) ist.

Schritt 1: Der führende Term des Dividenden \(\displaystyle p(x) = -x^3+1\) ist \(\displaystyle -x^3\), während der führende Term für den Divisor \(\displaystyle s(x) = x-1\) gleich \(\displaystyle x\) ist.

Der Term, den wir mit \(x\) multiplizieren müssen, um den führenden Term des Dividenden zu erhalten, ist also \(\displaystyle \frac{ -x^3}{ x} = -x^2\), also addieren wir diesen Term zum Quotienten. Außerdem multiplizieren wir diesen Term mit dem Divisor, um \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\) zu erhalten, den wir vom Dividend subtrahieren müssen:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]

Schritt 2: Der führende Term des aktuellen Rests \(\displaystyle -x^2+1\) ist \(\displaystyle -x^2\), und wir wissen, dass der führende Term des Divisors \(\displaystyle x\) ist.

Der Term, den wir mit \(x\) multiplizieren müssen, um den führenden Term des aktuellen Rests zu erhalten, ist also \(\displaystyle \frac{ -x^2}{ x} = -x\), also addieren wir diesen Term zum Quotienten. Außerdem multiplizieren wir dies mit dem Divisor, um \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\) zu erhalten, das wir vom aktuellen Rest subtrahieren müssen:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]

Schritt 3: Der führende Term des aktuellen Rests \(\displaystyle -x+1\) ist \(\displaystyle -x\), und wir wissen, dass der führende Term des Divisors \(\displaystyle x\) ist.

Der Term, den wir mit \(x\) multiplizieren müssen, um den führenden Term des aktuellen Rests zu erhalten, ist also \(\displaystyle \frac{ -x}{ x} = -1\), also addieren wir diesen Term zum Quotienten. Außerdem multiplizieren wir dies mit dem Divisor, um \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\) zu erhalten, das wir vom aktuellen Rest subtrahieren müssen:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]

Der Quotient ist also \(\displaystyle q(x) = -x^2-x-1\), und der Rest ist \(\displaystyle r(x) = 0\).

Nach dem Teilen haben wir uns bei der Faktorisierung mit fortgeschritten

\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]

Aber da der gefundene Quotient \(\displaystyle -x^2-x-1\) quadratisch ist, können wir seine Wurzeln finden, um zu sehen, ob wir ihn auf dem reellen Feld faktorisieren können.

Wir müssen die folgende quadratische Gleichung \(\displaystyle -x^2-x-1=0\) lösen.

Verwenden der quadratischen formel

Für eine quadratische Gleichung der Form \(a x^2 + bx + c = 0\) werden die Wurzeln mit Hilfe der folgenden Formel berechnet:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall ist die Gleichung, die wir lösen müssen, \(\displaystyle -x^2-x-1 = 0\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = -1\] \[b = -1\] \[c = -1\] \[\Delta = b^2 - 4ac = \displaystyle \left( -1\right)^2 - 4 \cdot \left(-1\right)\cdot \left(-1\right) = -3\]

Da in diesem Fall die Diskriminante \(\Delta = \displaystyle -3 < 0\) negativ ist, wissen wir, dass die gegebene Gleichung zwei verschiedene konjugierte komplexe Wurzeln hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]

Also finden wir das:

\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]

Nachdem wir also die Wurzeln des letzten quadratischen Teils gefunden haben, finden wir zwei komplexe Wurzeln, so dass wir den Term \(-x^2-x-1\) nicht im reellen Feld faktorisieren können, so dass wir den Prozess mit \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\) beenden.

Daher führt die Lösung von \(x\) für die gegebene Polynomgleichung zu den Lösungen \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), unter Verwendung von Faktorisierungsmathoden.

Überprüfen der hilfslösungen

Die Prüfung dieser Lösungen anhand der Hilfspolynomgleichung zeigt, dass nicht alle Lösungsvorschläge tatsächlich eine Lösung der ursprünglichen Gleichung sind. Die einzigen tatsächlichen Lösungen der ursprünglichen Gleichung sind:

\[x_1=0 \]
\[x_2=1 \]

Daher führt die Lösung von \(x\) für die gegebene Gleichung zu den Lösungen \(x=0,\,\,x=1\).

Grafisch

Es folgt die grafische Darstellung der erhaltenen Lösungen:

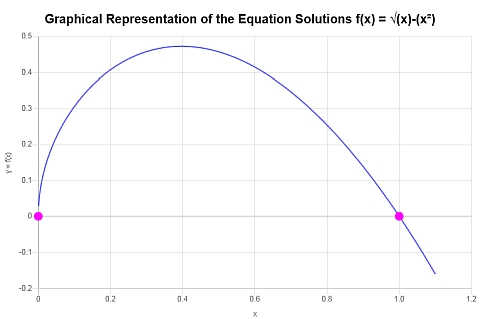
womit die Berechnung abgeschlossen ist.

Andere nützliche gleichungslöser

Beim Lösen von radikalen Gleichungen müssen Sie, anders als in dem Fall, in dem Sie Lösung lineare Gleichungen oder wenn Sie eine quadratische Gleichung lösen fällt in die Kategorie jener Gleichungen, die eine geschickte algebraische Manipulation erfordern, um x zu lösen.

Mit anderen Worten, es gibt kein "mach es so und es wird immer funktionieren". Die Art der Manipulation, die Sie vornehmen, hängt von der Struktur der Gleichung ab und kann von Fall zu Fall sehr unterschiedlich sein.

Ausdrücke vereinfachen ist immer eine gute Praxis, da Sie so Begriffe reduzieren, die die Gesamtstruktur der Gleichung durcheinander bringen könnten.