Gráfico polinomial

Use esta calculadora se precisar de ajuda para representar graficamente uma função polinomial. O processo é fácil: basta digitar a função polinomial que deseja representar graficamente. Você pode escrever algo como '3x^3 + x - 1', ou pode começar com o nome da função, como 'p(x) = 3x^3 + x - 1'.

Os coeficientes do polinômio fornecidos não precisam necessariamente ser inteiros, podem ser frações ou qualquer expressão algébrica válida. O polinômio que você fornecer pode vir simplificado ou não, não importa.

Então, uma vez fornecido o polinômio, você pode opcionalmente determinar os intervalos de valores de x que serão representados graficamente, e então clicar em "Calcular", e em breve, todas as etapas do processo serão mostradas.

funções polinomiais são um dos objetos mais importantes que você encontrará em Álgebra, bem como em Cálculo. Além disso, os polinômios levam à necessidade de resolver equações polinomiais, que têm muitas aplicações em todos os lugares, em todos os aspectos da vida, até mesmo além da matemática.

Noções básicas de funções polinomiais

Lembremos que uma função polinomial tem a seguinte forma:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

onde assumimos que \(a_n \ne 0\), e dizemos que o grau do polinômio neste caso é igual a \(n\), e o coeficiente principal é \(a_n\). A maneira leiga de definir o grau de um polinômio é que ele corresponde à maior potência presente na expressão polinomial.

Por exemplo, \(p(x) = 3x^2 + 2x - 1\) é um polinômio de grau 2, e seu coeficiente líder é 3. Agora, \(p(x) = \sin(3x^2 + 2x - 1)\) NÃO é um polinômio, por exemplo.

Como fazer gráficos de polinômios?

A representação gráfica de polinômios, em princípio, mostra o mesmo que a representação gráfica de qualquer outra função. Se você fosse fazer manualmente, você tabularia vários valores para x e y, e traçaria uma curva que passaria mais ou menos pelos pontos que você está obtendo em sua tabela.

Naturalmente, este método é um pouco primitivo, porque em geral não podemos conhecer necessariamente o gráfico completo de uma função apenas conhecendo um monte de pontos que estamos tabulando.

Felizmente, para polinômios a tarefa é um pouco mais fácil e, na realidade, podemos saber muito sobre seu gráfico conhecendo seu coeficiente líder e seu grau.

Etapas para representar graficamente funções polinomiais

O gráfico de um polinômio depende, em última análise, do coeficiente específico de cada polinômio. Mas podemos fazer algumas afirmações fortes sobre o comportamento final de polinômios e a existência de raízes reais.

Lembremos que o comportamento final de um polinômio é o comportamento do polinômio quando x é muito grande e negativo, e quando x é muito grande e positivo.

• Passo 1: Identifique a função polinomial e simplifique se puder, pois é mais fácil representar graficamente expressões que são simplificadas
• Passo 2: Você conhece as raízes do polinômio? Se essas são raízes reais, você conhece os pontos onde o polinômio cruza o eixo x, o que lhe dá uma forte referência gráfica
• Passo 3: Se o grau do polinômio for ímpar, o comportamento final será oposto para grandes valores negativos de x e grandes valores positivos de x. Se o coeficiente principal for positivo, para grandes valores negativos de x, o polinômio será muito grande e negativo, e para grandes valores positivos de x, o polinômio será muito grande e positivo. Se o coeficiente principal for negativo, para grandes valores negativos de x, o polinômio será muito grande e positivo, e para grandes valores positivos de x, o polinômio será muito grande e negativo
• Passo 4: Se o grau do polinômio for par, o comportamento final será o mesmo para grandes valores negativos de x e grandes valores positivos de x. Se o coeficiente líder for positivo, para grandes valores negativos e positivos de x, o polinômio será muito grande e positivo. Se o coeficiente principal for negativo, para grandes valores negativos e positivos de x, o polinômio será muito grande e negativo
• Estágio 5: Se o grau do polinômio for ímpar, o polinômio cruzará pelo menos uma vez o eixo x (portanto, terá pelo menos uma raiz real), enquanto que, para um grau par, o polinômio não necessariamente cruzará o eixo x
• Passo 6: Um polinômio de grau n cruzará o eixo x no máximo n vezes. Por exemplo, um polinômio de 4 graus 4 pode cruzar o eixo x no máximo 4 vezes

Assim, por exemplo, um polinômio cúbico pode cruzar o eixo x no máximo 3 vezes, mas não precisa.

Calculadora gráfica

Quais são as vantagens de usar uma calculadora gráfica? Vários. Isso não quer dizer que não seja uma boa habilidade ser capaz de esboçar com precisão um polinômio usando papel e caneta.

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

• Vantagem 1: Certifique-se de obter uma representação precisa do gráfico real do polinômio
• Vantagem 2: Você pode usá-lo para verificar seu próprio trabalho, para ter certeza de que está seguindo as etapas corretas
• Vantagem 3: Uma boa calculadora com escolha de uma janela apropriada para mostrar os aspectos mais relevantes do gráfico

Um bom gráfico pode dizer muito sobre as propriedades de uma função, e o mesmo vale para um polinômio. A representação gráfica de polinômios pode ajudá-lo a visualizar verdadeiramente que tipo de raízes o polinômio possui.

Dicas e truques

Tenha cuidado ao ler demais o que você vê em um gráfico polinomial. Você não pode dizer muito sobre raízes com multiplicidade, então nada substitui a função real.

Se você quiser experimentar outros tipos de funções, tente isso gráfico de funções ferramenta.

Exemplo: representação gráfica de funções polinomiais

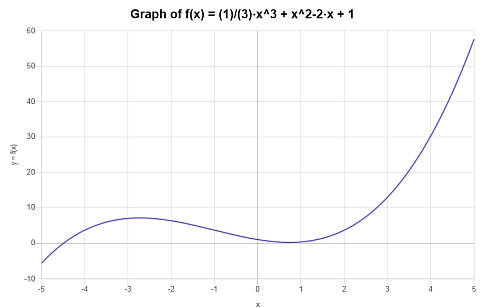
Faça o gráfico do seguinte polinômio: \(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)

Solução: Temos a seguinte expressão polinomial que precisamos calcular: \(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\).

A expressão fornecida é irredutível, então não há nada para simplificar.

O gráfico a seguir é obtido para a expressão polinomial fornecida no intervalo \([-5, 5]\):

Exemplo: gráfico polinomial

Simplifique e faça o gráfico: \(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)

Solução: Agora, precisamos trabalhar com: \(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\).

Obtém-se a seguinte simplificação:

o que conclui o processo de simplificação polinomial.

Assim, obtém-se o seguinte gráfico para \(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\) no intervalo \([-5, 5]\):

Exemplo: mais gráficos polinomiais

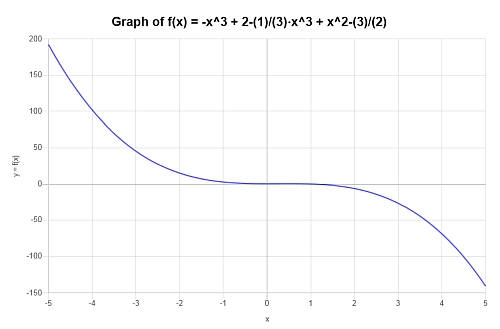
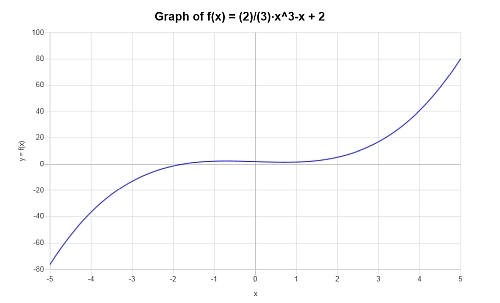
Encontre o gráfico do seguinte polinômio \( p(x) = \frac{2}{3} x^3 - x +2 \).

Solução: Para este exemplo, o polinômio fornecido é: \(\displaystyle \frac{2}{3} x^3 - x +2 \).

Nesse caso, a expressão fornecida é irredutível, portanto não há nada para simplificar.

O gráfico a seguir é obtido para a expressão polinomial fornecida no intervalo \([-5, 5]\):

Mais calculadoras polinomiais

A representação gráfica de polinômios é extremamente útil, pois nos mostra as principais características de seu comportamento em torno de suas raízes e seu comportamento final. A representação gráfica geralmente anda de mãos dadas com a identificação aproximada de onde as raízes podem estar, o que poderia ser usado com fatoração de polinômios também.

Embora possamos saber muito sobre o polinômio apenas por representá-lo graficamente, ainda precisamos passar pelo processo de tentar encontrar raízes racionais , como ponto de partida para resolvendo equações polinomiais com grau maior que 2 (este, que não são equações quadráticas ).

Adivinhar sistematicamente ou encontrar raízes racionais, emparelhado com o uso Divisão longa ou Divisão Sintética então para usar o teorema do fator pode levar a uma busca bem-sucedida de raízes polinomiais , mas essa abordagem nem sempre funciona e, muitas vezes, você precisa confiar na calculadora para encontrar aproximações numéricas.