Calculadora de divisão polinomial longa

Esta calculadora ajuda você no processo de conduzir uma divisão longa entre dois polinômios dados. Para isso, você precisa fornecer duas expressões polinomiais válidas. Esses polinômios podem já estar simplificados ou não, e a calculadora irá simplificá-los caso precise.

Quando dividindo polinômios você precisa fornecer dois polinômios, um para o qual você estará dividindo, que é chamado de dividendo, e o outro é o divisor.

Depois de fornecer dois válidos polinômios , o próximo passo seria clicar no botão "Calcular", que mostrará todo o cálculo correspondente necessário para a divisão longa desejada entre os polinômios fornecidos.

O processo de conduzir uma divisão de polinômios usando o Método Da Divisão Longa é um método relativamente simples, mas que requer uma abordagem muito organizada, para não se perder. Normalmente, funciona melhor usando uma abordagem tabular para mostrar as etapas correspondentes.

Uma abordagem mais simples é usada com Divisão Sintética , mas isso só se aplica quando o divisor tem grau um, então tem um alcance mais limitado

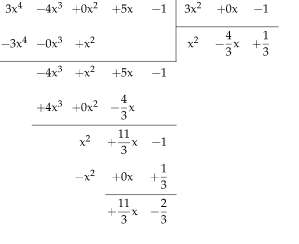
O que é um polinômio?

Um polinômio é um tipo de expressão simples que combina com somas e subtrações as potências inteiras de uma certa variável x (ou qualquer nome de variável escolhido), possivelmente multiplicado por constantes.

Por exemplo, a expressão \(p(x) = 2x^2 + x + 1\) é uma combinação dos termos \(2x^2\), \(x\) e \(1\) com adições de potências de x (observe que 1 é uma potência de x, como \(x^0 = 1\).

Por outro lado, \(f(x) = 2x^2 + \sin(x) + 1\) não é um polinômio, porque o termo \(\sin(x)\) não é potência de x.

Operações polinomiais

Polinômios, assim como números, podem ser operados com adição, subtração, multiplicação e divisão de polinômios . Adições e subtrações são simples de fazer, de forma bem intuitiva. Por exemplo, se você tiver dois polinômios, \(p(x) = 2x+1\) e \(q(x) = x^3 + 2x+ 3\), a adição do polinômio é obtida adicionando literalmente os termos como

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

Para subtrações, você também subtrai os termos correspondentes do polinômio que está sendo subtraído. Por exemplo, se você tiver dois polinômios, \(p(x) = 2x+1\) e \(q(x) = x^3 + 2x+ 3\), a subtração é feita como

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

A multiplicação é mais complicada, porque você precisa multiplicar os termos usando a propriedade distributiva:

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

A divisão é um pouco mais complicada, porque envolve a ideia de que um polinômio não pode dividir exatamente outro polinômio. Matematicamente, quando temos dois polinômios \(p(x)\) e \(s(x)\), e queremos dividir \(p(x)\) por \(s(x)\), procuramos um quociente \(q(x)\) e um resto \(r(x)\) (ambos polinômios), que possuem a propriedade \(p(x)= q(x)\cdot s(x) + r(x)\), com a condição de que o grau do polinômio \(r(x)\) é menor que o grau de \(s(x)\). Isso geralmente é chamado de Decomposição De Euclides .

O método da divisão longa

Assim, o Método da Divisão Longa é uma maneira sistemática de começar com dois polinômios que queremos dividir \(p(x)\) e \(s(x)\), então encontramos o quociente \(q(x)\) e um resto \(r(x)\) em tais uma maneira que

\[p(x)= q(x)\cdot s(x) + r(x)\]

Esse algoritmo é extremamente útil e, embora o problema pareça simples na aparência, não é difícil se perder se não usar uma abordagem sistemática, que garante chegar ao quociente e resto necessários.

Quais são os passos para fazer uma divisão longa?

• Passo 1: Identifique os dois polinômios p(x) e s(x) que você deseja dividir e identifique p(x) como o dividendo e s(x) como o divisor
• Passo 2: Verifique o grau do dividendo p(x) em relação ao grau de s(x). Se o grau de s(x) for maior que o grau de p(x), temos que o resto é o próprio dividendo p(x), e o quociente é zero: q(x) = 0, e pronto
• Passo 3: Nesse caso, assumimos que o grau do dividendo p(x) é maior ou igual ao grau da divisão s(x), caso contrário, teríamos parado no passo 2
• Passo 4: Precisamos conduzir um processo iterativo para encontrar um resto temporário, até chegarmos a um resto que tenha um grau menor que o grau de s(x)
• Estágio 5: O restante temporário ou interino é atualizado sempre, primeiro encontrando a razão entre o termo mais alto do restante temporário atual e o divisor s(x). Essa razão (que é um termo de potência) multiplica então s(x), e o resultado dessa multiplicação é subtraído do resto temporário atual, levando a um resto atualizado
• Passo 6: Esse processo continua até que o restante tenha um grau menor que o de s(x). Em cada etapa da iteração, o grau do restante temporário é reduzido em pelo menos 1, de modo que o processo é garantido para terminar

Ao final, o processo de dividindo dois polinômios é reduzido para calcular as multiplicações são somas de polinômios, que é praticamente o que acontece com os números. O método de divisão longa para polinômios é a extensão da forma como dividimos números para polinômios.

Como a divisão longa está conectada com a descoberta de raízes de uma equação polinomial

Suponha que p(x) seja o dividendo que você deseja dividir e s(x) seja o divisor. De acordo com o método da Divisão Longa, você poderá encontrar um quociente q(x) e um resto r(x) de modo que:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

Mas às vezes acontece que o resto é r(x) = 0, e nesse caso dizemos que s(x) divide p(x) (ou divide p(x) exatamente). Então, quando r(x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

Isso indica que para encontrar as raízes de p(x) = 0, podemos resolver q(x) = 0 e s(x) = 0, separadamente, que são equações mais simples de resolver.

Vantagens desta calculadora de divisão longa

Como mencionei antes, a divisão longa não é muito difícil, mas requer uma abordagem sistemática. Uma grande vantagem de usar um calculadora de divisão como este é que você obterá todas as etapas do processo mostradas

Pode não ser essencial saber conduzir os passos você mesmo, mas esta calculadora permite que você veja como isso é feito, com cada passo explicando, tirando o mistério de obter o resto e o quociente de, digamos, uma calculadora digital, que dará você a resposta sem mostrar os passos.

Uma calculadora de divisão longa com etapas mostrando todo o trabalho garante que você tenha uma ideia clara do que está acontecendo com o cálculo.

Exemplo: calculando a divisão de polinômios

Calcule a divisão dos seguintes polinômios: \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) e \(s(x) = x+3\).

Solução: O seguinte polinômio foi fornecido: \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\), que precisa ser dividido pelo polinômio \(\displaystyle s(x) = x+3\).

Observe que o grau do dividendo é \(\displaystyle deg(p) = 3\), enquanto o grau do divisor é \(\displaystyle deg(s)) = 1\).

Passo 1: O termo inicial do dividendo \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) é \(\displaystyle \frac{1}{3}x^3\), enquanto o termo inicial do divisor \(\displaystyle s(x) = x+3\) é igual a \(\displaystyle x\).

Então, o termo que precisamos multiplicar \(x\) para chegar ao termo inicial do dividendo é \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\), então adicionamos esse termo ao quociente. Além disso, multiplicamos isso pelo divisor para obter \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\), que precisamos subtrair ao dividendo:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Passo 2: Nesse caso, o termo inicial do restante atual \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) é \(\displaystyle -1x^2\) e sabemos que o termo inicial do divisor é \(\displaystyle x\).

Então, o termo que precisamos multiplicar \(x\) para chegar ao termo inicial do resto atual é \(\displaystyle \frac{ -1x^2}{ x} = -x\), então adicionamos esse termo ao quociente. Além disso, multiplicamos isso pelo divisor para obter \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\), que precisamos subtrair do lembrete atual:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Passo 3: Nesse caso, o termo inicial do restante atual \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) é \(\displaystyle \frac{17}{4}x\) e sabemos que o termo inicial do divisor é \(\displaystyle x\).

Então, o termo que precisamos multiplicar \(x\) para chegar ao termo inicial do resto atual é \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\), então adicionamos esse termo ao quociente. Além disso, multiplicamos isso pelo divisor para obter \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\), que precisamos subtrair do lembrete atual:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

o que conclui este cálculo, já que o grau do resto atual \(r(x) = -\frac{163}{12}\) é menor que o grau do divisor \(s(x) = x+3\).

Conclusão: Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that