Gráfico de função trigonométrica

As funções trigonométricas têm a propriedade de repetir seu comportamento. Ou seja, eles são periódicos. Matematicamente, isso significa que existe um número $P$ com a propriedade que

$$f(x+P) = f(x)$$

para todos os valores de $x$. Esse número $P$ é chamado de período . Tudo isso está dizendo é que o comportamento da função se repete em gráficos trigonométricos a cada $P$ unidades no eixo x.

Observe que todas as funções trigonométricas fornecidas para esta calculadora, o argumento $x$ é considerado medido em radianos .

Exemplo de funções periódicas

Por exemplo, para o caso da função seno, $f(x) = \sin x$, o gráfico é mostrado abaixo:

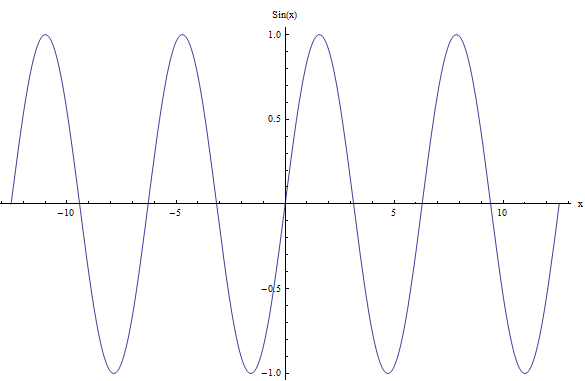
Você pode ver que o comportamento da função se repete. De fato, você pode tomar qualquer intervalo de comprimento $2\pi$ e o próximo intervalo de comprimento $2\pi$ será idêntico ao anterior, em termos da forma da função.

Por que isso acontece? Porque $\sin(x + 2\pi) = \sin(x)$, para todo $x$, e então a função é periódica.

O que posso representar graficamente com este plotter de funções trigonométricas?

Você pode plotar qualquer função trigonométrica. O uso mais comum é para gráficos de seno e cosseno, mas você pode usá-lo para qualquer função trigonométrica.

Você verá que funções periódicas podem se tornar mais complexas combinando-as com outras expressões algébricas.

Por exemplo, qual é o comportamento da função $f(x) = 3\sin(2x+1)-4$ Bem, é mesmo periódica? Sim, pode apostar. O comportamento da função $f(x) = 3\sin(2x+1)-4$ é em tudo semelhante ao da função $f(x) = \sin x$.

Este gráfico de função trigonométrica ajudará você a encontrar o gráfico e as características específicas (período, frequência, amplitude, deslocamento de fase e deslocamento vertical) de funções trigonométricas mais complexas, como $f(x) = 3\cos(\pi(x-2)+3)-\frac{\pi}{4}$

Os parênteses importam?

A resposta curta é: DEPENDE. Às vezes, você terá uma expressão simples onde apenas somas ou apenas multiplicações estão presentes, caso em que o propriedade associativa pode ser usado. Mas quando há operações mistas com muita frequência, você não pode omitir ou alterar um parêntese sem quebrar a função ou alterá-la.

Calculadoras gráficas

Este gráfico lida apenas com funções trigonométricas. Em ordem de gráfico outras funções , você pode usar nosso plotter de função geral , que assumirá qualquer função, não apenas as trigonométricas.

Exemplo de gráfico trigonométrico

Pergunta : Considere a função $f(x) = \sin(3x-2)$. Encontre o período, a frequência, a amplitude e a mudança de fase. Além disso, forneça um gráfico da função.

Solução:

A seguinte função foi fornecida:

$$f(x) = \sin\left(3x-2\right)$$

Com base no argumento da função trigonométrica passada, a frequência e o período são calculados da seguinte forma:

$$\begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}$$

e também

$$\begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}$$

Com base na função trigonométrica fornecida, $f(x) = \sin\left(3x-2\right)$, obtemos que:

• A amplitude neste caso é $A = 1$.

• A mudança de fase é igual a $\displaystyle\frac{2}{3} = 0.6667$.

• O deslocamento vertical é igual a $0$.

Com base nas informações acima, obtém-se o seguinte gráfico: