Solventes Álgebra

Funções polinomiais

Instruções: Use esta calculadora de função polinomial para calcular uma operação algébrica envolvendo polinômios. Por favor, digite uma expressão que envolva alguma operação com polinômios, e a calculadora fará isso, simplificará o resultado e lhe dará o gráfico, mostrando todos os passos.

Funções polinomiais

Isto calculadora de funções polinomiais irá ajudá-lo a calcular funções polinomiais, calculando e simplificando qualquer expressão polinomial que você fornecer.

Você pode fornecer qualquer tipo de expressão envolvendo polinômios, e o cálculo será realizado e as etapas de simplificação necessárias serão tomadas, de modo a deixar uma função polinomial em sua forma mais compacta. Em seguida, um gráfico polinomial será fornecido

Então, uma vez fornecida uma expressão polinomial válida, você pode clicar no botão abaixo, o botão "Calcular", e todas as etapas necessárias do processo serão mostradas.

A álgebra de frações envolve a conversão de frações, como o uso de denominador comum e o uso de regras aritméticas básicas. Em suma, o processo de cálculo pode ser trabalhoso, embora possa ser feito sistematicamente, sem grandes problemas.

O que é uma função polinomial?

Polinômios, na explicação mais simples, são as funções que consistem apenas em potências de \(x\), possivelmente multiplicadas por constantes numéricas, que são adicionadas (ou subtraídas) entre si. Por exemplo, \(p(x) = x^3 + 2x^2 + 1\) é uma função polinomial, pois consiste nas potências de \(x\) multiplicadas por constantes, somadas. Neste caso, \(1 = x^0\) então uma constante também é uma potência de \(x\). :

Em geral, uma função polinomial tem a seguinte forma:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

com \(a_n \ne 0\). Neste caso, dizemos que o grau do polinômio (ou sua ordem) é \(n\), que é a maior potência presente na função polinomial.

Além disso, o coeficiente \(a_n\) é chamado de coeficiente líder , e \(a_n x^n\) é chamado de termo principal . O coeficiente líder e o grau de um polinômio determinarão seu comportamento final (isto é, o comportamento quando o valor absoluto de x é grande).

Quais são as etapas para trabalhar com uma função polinomial?

Passo 1: Identifique claramente a expressão com a qual deseja trabalhar, expanda e simplifique
Passo 2: Verifique se os termos que envolvem a variável x correspondem apenas a potências de x, senão pára, não é um polinômio
Passo 3: Certifique-se de que todas as potências de x sejam multiplicadas por constantes (que podem ser '1') e que esses termos apareçam como adicionados ou subtraídos na expressão

É importante certificar-se de que você tem uma função polinomial, para poder aplicar resultados exclusivos a polinômios, como o teorema do fator , o teorema do resto e Teorema do Racional Zero , que são extremamente úteis para encontrar as soluções de equações polinomiais, que são amplamente utilizadas em diferentes aplicações.

Além disso, a vantagem de lidar com funções polinomiais é que você pode conduzir facilmente divisão de polinômios , seja usando Divisão longa ou Divisão Sintética caso o divisor seja linear.

Existem funções polinomiais importantes?

De fato. Existem os notórios polinômios de grau 2, que chamamos de polinômios quadráticos , que são extensivamente estudados em álgebra básica. A razão para isso é que eles podem ser totalmente analisados usando fórmulas precisas. Por exemplo, você tem um fórmula do vértice , e a famosa fórmula quadrática é usada para encontrar raízes para polinômios quadráticos :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Há também os polinômios de grau 2, que chamamos de polinômios cúbicos , que também possuem fórmulas explícitas, mas que geralmente são consideradas mais complexas e normalmente não são abordadas em cursos básicos de álgebra.

O que eu sei sobre o comportamento final de um polinômio?

O comportamento final de um polinômio dependerá, em última análise, do próprio polinômio, mas algumas coisas podem ser ditas com base em seu grau

Fato 1: Para polinômios quadráticos, o gráfico abre para cima (se o coeficiente líder for positivo) ou para baixo (se o coeficiente líder for negativo), e a função converge para infinito ou menos infinito (dependendo do sinal do coeficiente líder) em ambos os lados
Fato 2: Para polinômios com grau ímpar (por exemplo, com grau 3) terão pelo menos uma raiz real, e a função converge para infinito de um lado e para menos infinito do outro lado
Fato 3: Para polinômios com grau par (por exemplo, com grau 4), não haverá necessariamente raízes reais (um ponto que o gráfico cruza no eixo x), e a função converge para infinito ou menos infinito (dependendo de o sinal do coeficiente principal) em ambos os lados

Assim, os polinômios são grandes para grandes valores de x, e se seus valores são positivos ou negativos para positivo de x (em seu comportamento final) depende do sinal do coeficiente principal.

Dicas: quais são os benefícios de usar uma calculadora de funções polinomiais

As calculadoras polinomiais podem garantir que você chegue à resposta certa. De fato, cálculos polinomiais não são complicadas, mas podem ser complicadas e não é difícil cometer erros.

Evite erros algébricos certificando-se de verificar seu trabalho com esta calculadora, para garantir a consistência da resposta final e as etapas usadas para chegar lá.

Exemplo: função polinomial

Calcule a seguinte função polinomial \((x-3)(x-1)(x-4)\)

Solução: Temos a seguinte expressão polinomial que precisamos calcular: \(\displaystyle (x-3)(x-1)(x-4)\).

Obtém-se o seguinte cálculo:

\( \displaystyle \left(x-3\right)\left(x-1\right)\left(x-4\right)\)

Observe that \((x-3) \cdot (x-1) = x^2-1x-3x+3\cdot 1 = x^2-4x+3\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \left(x^2-4x+3\right)\left(x-4\right)\)

Observe that \((x^2-4x+3) \cdot (x-4) = x^2x-4x^2-4x^2+4\cdot 4x+3x-3\cdot 4 = x^3-8x^2+19x-12\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-8x^2+19x-12\)

o que conclui o processo de simplificação polinomial.

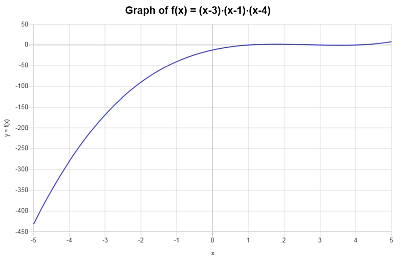
O seguinte gráfico é obtido para \(\displaystyle x^3-8x^2+19x-12\) no intervalo \([-5, 5]\):

Exemplo: cálculo de função polinomial

Esta é uma função polinomial: \(\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)

Solução:

Temos a seguinte expressão polinomial que precisamos calcular: \(\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\).

Obtém-se o seguinte cálculo:

\( \displaystyle \frac{1}{3}x^3+\frac{5}{4}\left(x-3\right)\left(x-\frac{5}{6}\right)\)

We get that \((x-3) \cdot (x-\frac{5}{6}) = x^2-\frac{5}{6}x-3x+3\cdot \frac{5}{6} = x^2-\frac{23}{6}x+\frac{5}{2}\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}x^3+\frac{5}{4}\left(x^2-\frac{23}{6}x+\frac{5}{2}\right)\)

We get that \((\frac{5}{4}) \cdot (x^2-\frac{23}{6}x+\frac{5}{2}) = \frac{5}{4}x^2-\frac{5}{4}\cdot \frac{23}{6}x+\frac{5}{2}\cdot \frac{5}{4} = \frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\), by using the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\)

que encerra o processo de simplificação.

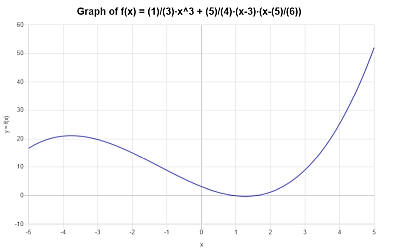
Graficamente, obtém-se o seguinte para a função simplificada \(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\) no intervalo \([-5, 5]\):

Exemplo: usando uma calculadora polinomial

Calcule \( x^2 - (2x - 1)x \).

Solução: Neste exemplo final temos \(\displaystyle x^2 - (2x - 1)x \), que precisamos simplificar.

Obtém-se o seguinte cálculo:

\( \displaystyle x^2-\left(2x-1\right)x\)

Notice that \((2x-1) \cdot (x) = 2x^2-1x = 2x^2-x\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^2-2x^2+x\)

Putting together the terms with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle x+\left(1-2\right)x^2\)

Operating the terms that were grouped with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle x-x^2\)

o que encerra a simplificação.

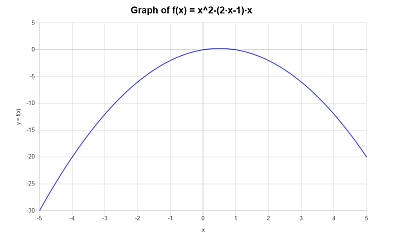
O seguinte gráfico é obtido para \(\displaystyle -x^2+x\) no intervalo \([-5, 5]\):

Mais calculadoras de álgebra

As funções polinomiais são literalmente a peça central da álgebra. Para aplicações básicas, polinômios quadráticos terá um papel fundamental e Economia, Física e Engenharia.

As funções polinomiais têm propriedades extremamente poderosas, especialmente envolvendo o cálculo de raízes polinomiais , que têm um forte significado em aplicativos.