O conceito de função é extremamente importante e absolutamente onipresente na matemática. É por isso que precisamos dar uma boa pincelada, antes de tentar entender algumas das coisas boas que virão depois, quando nos aprofundarmos nos tópicos de Cálculo, como diferenciação e integração.

O QUE É UM CONJUNTO?

O primeiro elemento que precisamos entender é o conceito de um conjunto . Um conjunto é simplesmente uma coleção de elementos. Então, um conjunto é simplesmente definido por meio de saber quais elementos pertencem ao conjunto e quais elementos não. Parece ser uma tarefa super simples e a teoria do conjunto deveria ser simplesmente reduzida a regras inequívocas para determinar quais elementos pertencem a um conjunto.

Por exemplo, vamos definir o conjunto de números pares e chamá-lo de \(E\). Por que é mesmo um conjunto? Porque tem uma regra inequívoca para determinar quais elementos pertencem a \(E\): Um número real \(x\) pertence a \(E\) se for divisível por 2. A regra funciona inequivocamente para cada número real único determinando se pertence ou não a \(E\). Por que digo “inequivocamente” e continuo repetindo. Porque é importante. Significa inequivocamente que não há como concluir que um dado \(x\) pertence e não pertence a \(E\). Infelizmente, às vezes as coisas vão além da nossa imaginação. Ao contrário da nossa intuição, um conjunto definível com uma regra simples de pertencimento pode levar a uma classificação de pertencimento ambígua (contraditória), como mostrado por Bertrand Russell em seu famoso paradoxo. Russell mostrou que uma definição mais cuidadosa do que é um conjunto deve ser usada.

Para todos os fins práticos, vamos pensar em um conjunto como uma coleção de elementos, definíveis por uma regra de pertencimento .

O QUE É O PRODUTO DE DOIS CONJUNTOS?

Sejam \(A\) e \(B\) conjuntos, no contexto da definição dada acima. O produto \(A\times B\) de dois conjuntos é outro conjunto, que é definido como o conjunto de todos os pares ordenados possíveis da forma \(\left( a, b \right)\), onde \(a\) pertence a \(A\) e \(b\) pertence a \(B\). Portanto, \(A\times B\) é um conjunto, e seus elementos são pares ordenados da forma \(\left( a ,b \right)\). Não deixe essa notação impressionar você. Quando digo "pares ordenados da forma \(\left( a, b \right)\)", o símbolo \(\left( a, b \right)\) é um símbolo inventado, para indicar um elemento que é composto de duas entidades \(a\) e \(b\), e identificar o primeiro elemento como sendo \(a\), e o segundo elemento como sendo __XYZ_F . É isso aí. Em vez de \(\left( a,b \right)\), poderíamos ter escolhido o símbolo \(a\_b\), e teria funcionado bem.

Você terá que me perdoar, mas eu tenho que escrever a definição matemática do produto de dois conjuntos (podemos multiplicar conjuntos também ... o que você achou, nós pararíamos apenas com números, uh?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

A razão pela qual escrevo a definição é para você olhar para ela e reconhecer como, usando uma notação muito compacta, estamos dizendo exatamente o mesmo que defini com as palavras no parágrafo acima. Espero que você diminua o medo de ler declarações matemáticas. Os matemáticos podem ser pessoas funky às vezes, mas eles encontram notações boas, inequívocas e compactas. E, conseqüentemente, a linguagem matemática é SUPER fácil de ler. Certo? Certo? Por favor me diga que estou certo ...

Uma nota lateral, por razões históricas, o produto de dois conjuntos \(A\times B\) é normalmente referido como um produto cartesiano .

AGORA, A DEFINIÇÃO DE UMA FUNÇÃO (FINALMENTE)

Ok, eu menti, há mais uma etapa antes de definir o que é uma função. Precisamos definir o conceito de relação . O que é uma relação? Além de seu uso comum como palavra em inglês, uma relação é simplesmente um subconjunto de um produto cartesiano. QUALQUER subconjunto de um produto cartesiano é uma relação. Então, se \(A\) e \(B\) são conjuntos, um conjunto \(R\) é uma relação se \(R\subseteq A\times B\). Como qualquer conjunto pode ser considerado um subconjunto de si mesmo, todos os produtos cartesianos são relações em si.

Coloque em uma moldura:

Uma relação é um conjunto que é um subconjunto de um produto cartesiano

Deixe-nos ser mais gráficos. Considere o conjunto \(A=\left[ 0,1 \right]\) (que são todos os números reais que são maiores ou iguais a 0, e eles também são menores ou iguais a 1). O que é o produto cartesiano \(A\times A\)? Vamos repetir o que acabamos de aprender. O produto cartesiano \(A\times A\) é \(\left[ 0,1 \right]\times \left[ 0,1 \right]\)neste caso é o conjunto de todos os pares\(\left( x, y \right)\), em que \(x\) e \(y\) pertencem a \(\left[ 0,1 \right]\). Os produtos cartesianos são normalmente fáceis de representar graficamente. Observe a região sombreada abaixo:

Agora, o que faria uma relação? Podemos “esculpir” tudo o que quisermos da região sombreada acima, e o que resta é uma relação em \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Por exemplo, podemos cortar os “cantos” para obter a seguinte sub-região:

A região (conjunto) acima é uma relação. Por quê? Porque é um subconjunto do produto cartesiano \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Mas podemos extrair ainda mais. Que tal esculpir um quarto de círculo? Veja a região abaixo.

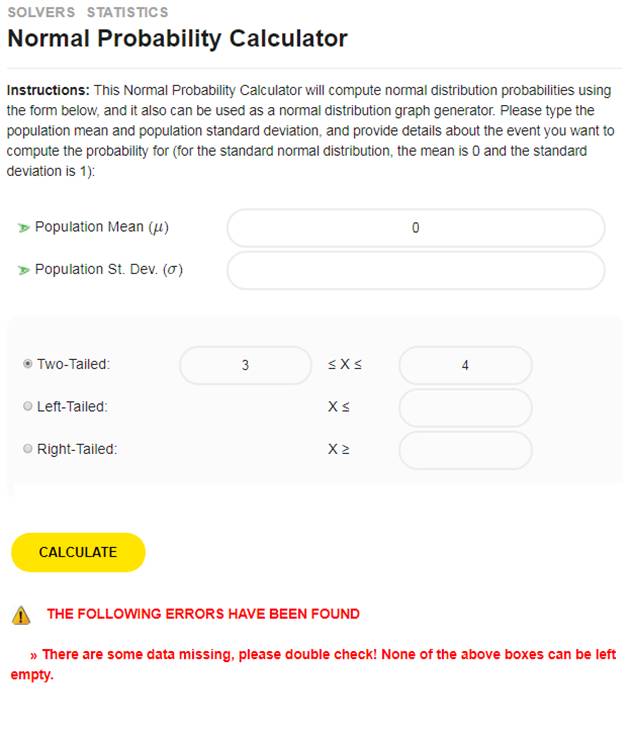
A região (conjunto) acima é uma relação. Por quê? Novamente, porque é um subconjunto do produto cartesiano \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

Agora, deixe-me dar um exemplo de duas relações em \(\left[ -1,1 \right]\times \left[ -1,1 \right]\). Veja os gráficos abaixo:

Relação 1

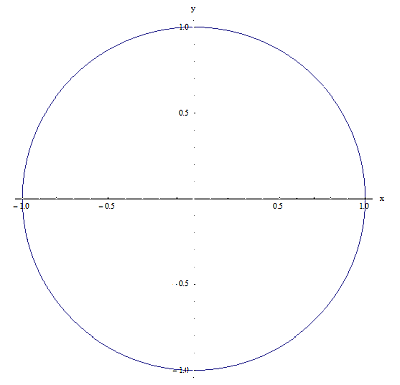
Relação 2

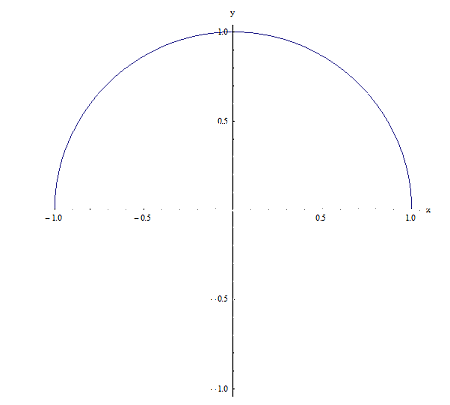
Ambos são obviamente relações (porque ambos estão contidos no produto cartesiano \(\left[ -1,1 \right]\times \left[ -1,1 \right]\), mas têm uma diferença fundamental: Para a Relação 1, para um determinado ponto x em \(\left[ -1,1 \right]\), há dois pontos \({{y}_{1}}\) e \({{y}_{2}}\) que têm a propriedade que \(\left( x,{{y}_{1}} \right)\) e __XYZ_F para a relação 1. Por exemplo para x = 0, existem dois pontos \({{y}_{1}}=1\) e \({{y}_{2}}=-1\) tais que \(\left( 0,1 \right)\) e\(\left( 0,-1 \right)\) pertencem à relação 1. Agora, para a relação 2 esse não é o caso porque, por exemplo, para x = 0 é apenas \(y=1\) que faz com que o ponto \(\left( 0,1 \right)\) pertença à relação 1.

Finalmente podemos definir uma função: Uma função \(R\) é um conjunto que é uma relação e também tem a propriedade de que se o ponto \(\left( x,y \right)\) pertencer a \(R\), então não há outro ponto \(\bar{y}\) diferente de \(y\) que tem a propriedade que \(\left( x,\bar{y} \right)\) pertence a \(\left( x,\bar{y} \right)\) também. Em outras palavras, uma função é uma relação com o requisito extra de que cada \(x\) em seu domínio esteja associado a apenas um \(y\).

Como saber diferenciar entre uma função e uma relação?

Aparelhos! Usamos um pequeno truque chamado “Teste da Linha Vertical”: desenhamos uma linha vertical imaginária, e fazemos uma varredura movendo-a da esquerda para a direita completamente, e fazendo um mapa mental de onde a linha vertical intercepta a relação.

• Se em QUALQUER ponto, a linha vertical intersecta a relação em MAIS de um ponto, então a relação falha no teste da linha vertical, e então a relação não é uma função

• Se em QUALQUER ponto, a linha vertical não intercepta a relação em qualquer lugar em MAIS de um ponto, então a relação passa no teste da linha vertical, e então a relação é uma função

Veja os dois exemplos abaixo:

Exemplo 1: falha no teste de linha vertical porque a linha vertical mostrada na figura cruza a relação em mais de um ponto: NÃO É UMA FUNÇÃO

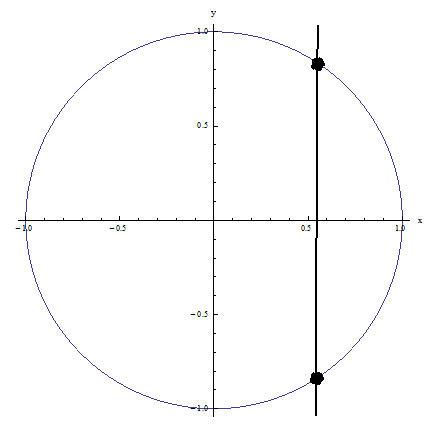
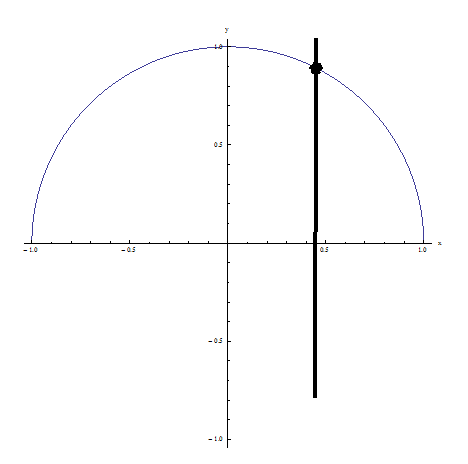
Exemplo 2: Passa no teste de linha vertical porque nenhuma linha vertical intercepta a relação em mais de um ponto: É UMA FUNÇÃO!

Existem muitas aplicações gráficas que podem ser realizadas com funções, incluindo o cálculo de assíntotas horizontais , assíntotas verticais e assíntotas inclinadas, se aplicável.