Fator por agrupamento
Fator por agrupamento é uma excelente forma de fatorar uma expressão, sem a necessidade de resolver uma equação polinomial, que pode ser difícil de resolver.
O único problema de fatorar por agrupamento é que não existe uma receita ou estratégia que lhe dê o agrupamento adequado necessário. Ou, pior ainda, pode não haver uma forma clara de agrupamento para realizar uma fatoração.
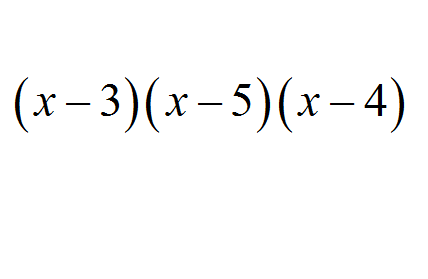
Neste tutorial, vamos nos concentrar nos casos especiais em que o agrupamento ajudará a fatorar uma expressão algébrica, embora a verdade seja que nem sempre é possível fazer isso. Para um tratamento mais geral, confira este tutorial em como fatorar .
As condições exigidas para fatoração por agrupamento
É assim que funciona a fatoração por agrupamento:
Precisamos procurar algumas dicas para usar esse tipo de fatoração. Para começar, esperaremos ter uma expressão algébrica com um número par de termos maior que 2 (então 4, 6, etc.) e, em seguida, tentar agrupar.
Como dissemos, não existem regras fixas, e você precisa jogar de ouvido, seguindo estas duas etapas.
Passo 1:
Agrupe o primeiro e o segundo mandato, o terceiro e o quarto mandato e assim por diante.
Passo 2:
Agora, tente fatorar todos os pares que você agrupou na Etapa 1. Observe que pode haver mais de uma maneira de fatorar.
Etapa 3:
Veja se os fatores obtidos na Etapa 2 são todos iguais; nesse caso, você pode fatorá-los.
Passo 4:
Se as etapas anteriores não funcionarem, tente o truque de "adicionar zero": às vezes, as coisas vão dar certo se você adicionar algo e também subtrair da expressão.
Ao adicionar e subtrair o mesmo termo, o efeito líquido é o mesmo que adicionar (ou seja, deixando a expressão como antes)
EXEMPLO 1
Fatorar usando o método de Fator por Agrupamento do seguinte polinômio
\[6x^3 + 3x^2 - 4x -2\]RESPONDA:
Precisamos usar as etapas que definimos acima. Observe que essas etapas não são imutáveis, mas são uma orientação útil para você seguir:
Passo 1: Agrupamos o primeiro e o segundo termos e também o terceiro e o quarto termos, de modo que obtemos
\[6x^3 + 3x^2 - 4x -2 = (6x^3 + 3x^2) - (4x + 2)\]
Passo 2: O termo \(6x^3 + 3x^2\) é fatorado como \(6x^3 + 3x^2 = 3x^2(2x+1)\), e o termo \(4x + 2\) é fatorado como \(4x + 2 = 2(2x+1)\), então obtemos:
\[6x^3 + 3x^2 - 4x -2 = (6x^3 + 3x^2) - (4x + 2) = 3x^2(2x+1) - 2(2x+1) \]
Etapa 3: Agora podemos ver como os dois grupos que fatoramos têm um fator comum, que é \(2x+1\), que pode ser fatorado pela propriedade distributiva. Portanto, o seguinte é obtido:
\[6x^3 + 3x^2 - 4x -2 = (3x^2-2)(2x+1)\]
que conclui o processo de factoring.
EXEMPLO 2
Resolva a seguinte equação: \(x^3 -6x^2 + 11x - 6 = 0\):
RESPONDA:
Visto que não sabemos realmente (embora seja possível) como encontrar a solução dessa equação cúbica, precisamos novamente usar as etapas para encontrar a fatoração por agrupamento de \(x^3 -6x^2 + 11x - 6 \), se possível:
Passo 1: Agrupamos o primeiro e o segundo termos e também o terceiro e o quarto termos, de modo que obtemos
\[x^3 -6x^2 + 11x - 6 = (x^3 -6x^2) + (11x - 6) \]
Passo 2: O termo \(x^3 -6x^2\) é fatorado como \(x^3 -6x^2 = x^2(x-6)\), e o termo \(11x - 6\) é fatorado como \(11x - 6= 11(x - 6/11)\), então obtemos:
\[x^3 -6x^2 + 11x - 6 = (x^3 -6x^2) + (11x - 6) = x^2(x-6) + 11(x - 6/11) \]
Etapa 3: Nesse caso, não há um fator comum, portanto o método não funcionou até agora.
Passo 4: Adicionamos \(0 = 2x - 2x\) e \(0 = 3x^2 - 3x^2\) que não afetará a expressão (estamos adicionando zeros), então obtemos:
\[ x^3 -6x^2 + 11x - 6 = x^3 -6x^2 + 11x - 6 + 2x - 2x + 3x^2 - 3x^2\] \[ = x^3 - 3x^2 -3x^2 + 9x +2x- 6 \] \[= (x^3 - 3x^2) -(3x^2 - 9x) +(2x- 6) \] \[= x^2(x - 3) -3x(x-3) +2(x- 3) \]
e agora temos o fator comum, \(x-3\) que estávamos procurando. Finalmente, fatorando \(x-3\), obtemos
\[\Large x^3 -6x^2 + 11x - 6 = (x^2-3x +2)(x- 3)\]Então, para resolver a equação original, também podemos resolver \((x^2-3x +2)(x- 3) = 0\) o que significa que \(x^2-3x +2 = 0\) ou \(x - 3\) = 0.
Da segunda equação, temos a única solução que é \(x = 3\). A partir da primeira equação, precisamos resolver:
\[ x^2-3x +2 = 0 \Rightarrow x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[ \Rightarrow x = \frac{3 \pm \sqrt{3^2 - 4(1)(2)}}{2(1)}\] \[ \Rightarrow x = \frac{3 \pm \sqrt{9-8}}{2}\] \[ \Rightarrow x = \frac{3 \pm 1}{2}\]o que implica que as outras soluções são \(x = (3-1)/2 = 1\) e \(x = (3+1)/2 = 2\).
Por que fatorar por agrupamento?
Lembremos que a fatoração é sempre uma boa coisa para resolver a equação, porque quando uma multiplicação de vários fatores é igual a zero, então as soluções da equação são encontradas definindo cada fator igual a zero.
Por exemplo, digamos que você queira resolver a equação \(x^3 + x^2 + 2x + 2 = 0\). Aposto que você não teria ideia se precisasse resolvê-lo usando meios algébricos.
Por quê? Porque esta é uma equação cúbica e resolvê-la é difícil. Existe uma fórmula, mas não é fácil. Que alternativas temos?
Bem, podemos fatorar por agrupamento, se possível. Veremos que de fato é possível neste caso. Seguiremos as etapas que foram delineadas acima:
Passo 1: O agrupamento do primeiro e do segundo mandato e também do terceiro e quarto termos leva a:
\[(x^3 + x^2) + (2x + 2) = 0\]
Passo 2: O termo \(x^3 + x^2\) é fatorado como \(x^3 + x^2 = x^2(x+1)\), e o termo \(2x + 2\) é fatorado como \(2x + 2 = 2(x+1)\), então obtemos:
\[x^2(x + 1) + 2(x + 1) = 0\]
Etapa 3: Agora vemos que os dois grupos que fatoramos têm um fator comum, que é \(x+1\), que pode ser fatorado pela propriedade distributiva, então obtemos:
\[(x^2+2)(x + 1)= 0\]
Portanto, o que descobrimos é que a expressão cúbica original foi fatorada como:
\[x^3 + x^2 + 2x + 2 = (x^2+2)(x + 1) = 0\]Dessa forma, podemos resolver a equação facilmente, definindo \(x^2 + 2 = 0\) ou \(x + 1 = 0\). Observe que, como \(x^2\) é sempre não negativo, obtemos \(x^2 + 2 \ge 2\) e nunca pode ser zero (pelo menos para \(x\) real).
Portanto, a única solução é \(x = -1\).
Então, isso veio de graça, usando fator por agrupamento. Caso contrário, teríamos que usar uma fórmula complicada de raiz cúbica, ou você teria que usar o método de "adivinhar as raízes", que vamos ser honestos, não é realmente um método.