Mais sobre o gráfico de probabilidade normal

Um gráfico de probabilidade normal é um gráfico normalmente usado para avaliar a normalidade da distribuição à qual os dados da amostra passada pertencem.

Existem diferentes tipos de gráficos de normalidade (PP, QQ e outras variedades), mas todos operam com base na mesma ideia. Os quantis teóricos de uma distribuição normal padrão são representados graficamente em relação aos quantis observados.

Portanto, se os dados da amostra vierem de uma população distribuída de normalidade , então o gráfico de probabilidade normal deve ser semelhante a 45 ^o reta, com variações aleatórias ao redor dela. Se esse não for o caso, e o padrão do gráfico de probabilidade normal se desviar significativamente/sistematicamente do gráfico de probabilidade normal, então deve-se suspeitar que a distribuição não é normal.

Como você calcula um gráfico de probabilidade normal?

Existem várias etapas concretas que você precisa seguir, em uma ordem específica para construir um gráfico de probabilidade normal

1. Neste caso concreto, os dados são ordenados em ordem crescente, e chamamos esses dados de \(X_1, X_2, ...., X_i , ...., X_n\).
2. Para cada \(X_i\) nesta sequência de dados ordenados, calculamos as frequências teóricas \(f_i\), que são aproximadas usando a seguinte fórmula:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. Em seguida, também calculamos \(z_i\), que é o z-score associado correspondente como
\[ z_i = \Phi^{-1}(f_i)\]
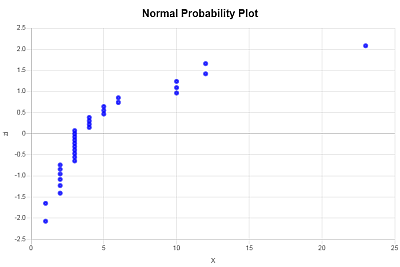
4. Em seguida, o gráfico de probabilidade normal é obtido plotando os valores X ordenados (seus dados de amostra) no eixo horizontal e os valores \(z_i\) correspondentes no eixo vertical.

Gráfico de probabilidade normal excel

Você pode traçar um gráfico de probabilidade normal no Excel, mas isso leva algum tempo

Calculadoras para distribuição normal e outras

Outros criadores de gráficos que você pode usar são nossos gráfico de distribuição normal , Criador de gráficos de dispersão ou o nosso Fabricante de cartas de Pareto .

Exemplo: cálculo de um gráfico de probabilidade normal

Pergunta : Você recebeu os seguintes dados de amostra: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 e 23. Construa um gráfico de probabilidade normal.

Solução:

Precisamos construir um gráfico de probabilidade normal. Estes são os dados de exemplo que foram fornecidos:

Observação:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

As frequências teóricas \(f_i\) precisam ser calculadas, bem como os escores z associados \(z_i\), para \(i = 1, 2, ..., 33\):

Observe que as frequências teóricas \(f_i\) são aproximadas usando a seguinte fórmula:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

onde \(i\) corresponde à posição no conjunto de dados ordenado e \(z_i\) é o z-score associado correspondente. Isso é calculado como

\[ z_i = \Phi^{-1}(f_i)\]

A tabela a seguir é obtida

Posição (i)	X (Ordem Ascendente)	f eu	por eu
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

O gráfico de probabilidade normal é obtido plotando os valores X (seus dados de amostra) no eixo horizontal e os valores \(z_i\) correspondentes no eixo vertical. O seguinte gráfico de normalidade é obtido: