Fonctions rationnelles

Cette calculatrice de fonctions rationnelles vous permettra d'analyser les points les plus pertinents d'une fonction rationnelle que vous fournissez, avec toutes les étapes indiquées. En règle générale, pour la plupart des fonctions rationnelles, vous pouvez trouver les intercepts, les asymptotes verticales et le graphique. Certaines fonctions rationnelles spécifiques ont également des asymptotes horizontales.

Le type de fonction que vous pouvez fournir est du type "f(x)=1/x - x", ou quelque chose impliquant des polynômes de degré supérieur comme "f(x) = (x^3-1)/(x^2+x)"

Une fois qu'une fonction rationnelle valide a été fournie, vous pouvez cliquer sur le bouton calculer, et toutes les étapes vous seront indiquées.

L'une des principales caractéristiques d'une fonction rationnelle est que l'on peut généralement réduire le calcul au problème suivant résolution d'équations polynomiales qui est l'un des types les plus "simples" de équations que vous pouvez résoudre .

Qu'est-ce qu'une fonction rationnelle ?

Une fonction rationnelle est une fonction qui fait intervenir la quotient de deux polynômes \(P(x)\) et \(Q(x)\), où le diviseur \(Q(x)\) n'est pas égal au polynôme zéro. La formule de la fonction rationnelle est donc

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

Par exemple, la fonction

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

est une fonction rationnelle, car elle est précisément le quotient de deux polynômes. Mais par exemple

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

n'est pas rationnel car le diviseur n'est pas un polynôme. Observez que lorsque nous disons que le diviseur \(Q(x)\) n'est pas égal au polynôme zéro, nous ne disons PAS que \(Q(x)\) ne peut pas avoir de zéros. Par exemple, dans le cas de \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \), le diviseur est \(Q(x) = x + 1\), qui a un zéro, à \(x = -1\).

Ce que nous ne voulons pas, c'est quelque chose comme

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

car bien que dans ce cas \(Q(x) = 0\) soit techniquement un polynôme, il s'agit du polynôme zéro (qui est zéro partout).

Étapes de calcul d'une fonction rationnelle

• Étape 1 : Tout d'abord, assurez-vous que vous disposez bien d'une fonction rationnelle, dont vous pouvez identifier le numérateur P(x) et le dénominateur Q(x)
• Étape 2 : Si vous ne trouvez pas strictement la structure décrite ci-dessus, vous vous arrêtez. Il se peut que vous deviez regrouper des termes par le biais de réductions algébriques .
• Étape 3 : Vous devez trouver les zéros réels de P(x) et Q(x), s'il y en a. Les conclusions trouvées seront étroitement liées aux zéros de P(x) et Q(x)
• Étape 4 : Pour trouver l'ordonnée à l'origine, vous évaluez la fonction à zéro, en calculant f(0). L'ordonnée à l'origine sera bien définie si x = 0 n'est pas un zéro de Q(x)
• Étape 5 : Pour trouver les ordonnées à l'origine, on obtient les zéros de P(x) qui ne sont pas des zéros de Q(x)
• Étape 6 : Pour trouver les asymptotes verticales, vous devez trouver les zéros de Q(x) qui ne sont pas des zéros de P(x)
• Étape 7 : Pour trouver les asymptotes horizontales, il faut que le degré de Q(x) soit supérieur ou égal au degré P(x)

Observez que, comme prévu, l'analyse d'une fonction rationnelle dépend de Trouver les zéros d'un polynôme et de rassembler toutes les conclusions. .

Remarquez que le domaine d'une fonction rationnelle est la ligne réelle entière, à l'exception des zéros du diviseur Q(x). S'il existe un zéro de Q(x) qui est également un zéro de P(x), la discontinuité peut être réparée. L'étendue d'une fonction rationnelle dépend des degrés de P(x) et de Q(x).

Pourquoi utiliser les fonctions rationnelles

Les fonctions rationnelles sont utilisées parce qu'elles sont des extensions naturelles des polynômes. On peut les considérer comme l'étape suivante dans la complexité d'une fonction. Comme nous le savons, expressions polynomiales sont parmi les fonctions les plus simples que l'on puisse trouver, mais elles sont aussi parmi les plus utiles.

Les équations rationnelles apparaissent généralement dans des problèmes de mélange plus avancés, et pourtant, elles sont étonnamment simples à traiter, à condition que les polynômes impliqués soient suffisamment simples. Nous savons que comment résoudre des équations quadratiques mais pour les polynômes de degré 3 et plus, les choses peuvent être plus compliquées.

Les fonctions polynomiales sont-elles aussi des fonctions rationnelles ?

Oui, si P(x) est un polynôme, alors P(x) est également rationnel, car nous pouvons l'écrire :

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

et Q(x) = 1 est un polynôme réel. L'inverse n'est pas vrai : une fonction rationnelle n'est pas nécessairement un polynôme. Comment cela se fait-il ? Parce que naturellement, à moins que Q(x) = 1, chaque fois que vous aurez \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), vous n'aurez pas que tous les termes seront des termes libres comme l'exige la définition d'un polynôme.

Plus formellement, en utilisant Théorème Du Reste , nous avons

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

où \(d(x)\) est un polynôme, mais \frac{r(x)}{Q(x)} ne l'est pas, car le degré de r(x) est inférieur à celui de Q(x).

Exemple : travailler avec des fonctions rationnelles

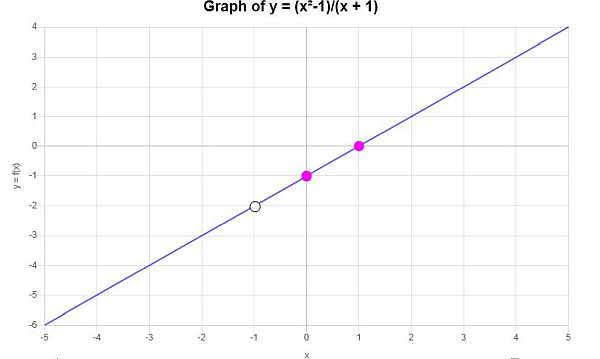
Trouvez les intercepts, les asymptotes et le graphique de : \(f(x) = \frac{x^2-1}{x+1}\)

Solution :

Nous avons reçu la fonction suivante :

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

Nous devons trouver les intercepts et les asymptotes, le cas échéant. Ensuite, le graphique de la fonction sera présenté.

Trouvons les zéros de la fonction donnée. Nous devons résoudre l'équation rationnelle suivante :

\[\frac{x^2-1}{x+1}=0\]

Observez que pour \(x \ne -1\) nous pouvons simplifier comme suit :

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Équation du numérateur auxiliaire

Maintenant, nous fixons le numérateur à zéro et nous trouvons les solutions. Ensuite, les racines qui ne rendent pas le dénominateur égal à zéro seront des solutions de l'équation rationnelle.

Le problème suivant doit être résolu pour trouver les racines du numérateur : \(x^2-1=0\)

Pour une équation quadratique de la forme \(a x^2 + bx + c = 0\), les racines sont calculées à l'aide de la formule suivante :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Dans ce cas, l'équation à résoudre est \(\displaystyle x^2-1 = 0\), ce qui implique que les coefficients correspondants sont :

\[a = 1\] \[b = 0\] \[c = -1\]

Tout d'abord, nous allons calculer le discriminant pour évaluer la nature des racines. Le discriminant est calculé comme suit :

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Puisque dans ce cas le discriminant est \(\Delta = \displaystyle 4 > 0\), qui est positif, nous savons que l'équation a deux racines réelles différentes.

En introduisant ces valeurs dans la formule des racines, nous obtenons :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

donc, nous trouvons que :

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Équation du dénominateur auxiliaire

Nous devons trouver les racines du dénominateur : \(x+1=0\)

Par conséquent, la résolution de \(x\) pour une équation linéaire donnée conduit à \(x=-1\).

Zéros du numérateur et du dénominateur

D'après l'analyse présentée ci-dessus, les zéros réels du numérateur de la fonction rationnelle donnée sont \( x_{ 1} = -1\) et \( x_{ 2} = 1\).

On constate également que le dénominateur a un zéro réel, qui est \( x_{ 1} = -1\).

Recherche d'intercepts x

En se basant sur les zéros du numérateur qui ne sont pas des zéros du dénominateur, on trouve qu'il y a une ordonnée à l'origine, qui est \(\left(1, 0\right)\).

Recherche des ordonnées à l'origine

En évaluant la fonction fournie à \(x = 0\), nous constatons que :

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

l'ordonnée à l'origine est donc \( \left(0, -1\right)\).

Asymptotes verticales

Après analyse des zéros, on conclut que la fonction n'a pas d'asymptotes verticales.

Asymptotes horizontales

Remarquez que le degré du numérateur est \(2\) et le degré du dénominateur est \(1\), puis, puisque le degré du polynôme du numérateur dépasse celui du dénominateur, nous concluons qu'il n'y a pas d'asymptote horizontale.

Le graphique suivant est obtenu :

Exemple : asymptotes horizontales

Cette fonction rationnelle a-t-elle une asymptote horizontale : \(f(x) = \frac{x^2-1}{x^2+1}\) ?

Solution : Il est clair que dans ce cas, la fonction est constituée du quotient de deux polynômes, et qu'ils ont tous deux un degré égal à 2. Ils ont donc le même degré et il y a donc une asymptote horizontale.

Nous pouvons également le constater en utilisant des limites :

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

ce qui implique que l'asymptote horizontale est \(y = 1\). Ceci conclut le calcul.

Calculatrices de fonctions utiles

Les fonctions sont des objets mathématiques fondamentaux qui résument la relation entre différentes variables. En utilisant une Calculatrice de fonctions peut vous aider à traiter systématiquement les fonctions qui peuvent être trop compliquées à manipuler à la main.

Représentation graphique des fonctions rationnelles est l'un des exemples de jouets les plus courants que les étudiants apprennent en algèbre et en calcul, et bien que les fonctions rationnelles n'apparaissent peut-être pas très souvent dans les applications, les compétences analytiques requises pour traiter les fonctions rationnelles peuvent s'avérer inestimables

Il en va de même pour Résolution d'équations rationnelles où les principes de manipulation des expressions algébriques et de réduction à leurs termes inférieurs seront extrêmement puissants pour l'acquisition de compétences plus avancées.

Si l'on parle de fonction, il ne faut pas oublier la calcul de la dérivée d'une fonction , l'intégration et d'autres techniques infinitésimales plus avancées.