Calculatrice d'équations rationnelles
Instructions : Utilisez cette calculatrice d'équations rationnelles pour calculer la solution de n'importe quelle équation rationnelle que vous fournissez, en montrant toutes les étapes. Veuillez saisir l'équation que vous souhaitez résoudre dans la case ci-dessous.
Résolution d'équations rationnelles
En utilisant cette calculatrice avec étapes, vous pourrez facilement résoudre des équations rationnelles. Pour ce faire, il vous suffit de fournir une équation rationnelle dans la case ci-dessus. Cette équation peut être aussi simple que "x^(1/2) = x^(1/4)", ou plus compliquée si nécessaire.
Ensuite, lorsque vous avez fini de taper ou de coller l'équation souhaitée, vous pouvez cliquer sur le bouton "Solve", ce qui aura pour effet de résoudre l'équation et montrera toutes les étapes du chemin.
Les équations rationnelles, comme d'autres types d'équations non linéaires, seront en général difficiles à résoudre, si tant est que vous puissiez les résoudre. En général, seules certaines Equations rationnelles les problèmes liés à l'utilisation de l'Internet, avec certaines structures spécifiques, pourront être résolus explicitement à l'aide de quelques astuces standard, comme l'utilisation de substitutions.

Qu'est-ce qu'une équation rationnelle ?
Une équation rationnelle est un type d'équation que l'on trouve en algèbre et dans laquelle, à un moment donné de l'équation, on voit un quotient de deux polynômes. Par exemple
\[\displaystyle \frac{x}{x+1} + 4 = 1\]est une équation rationnelle, à cause du terme \(\frac{x}{x+1} \). Techniquement, toutes les équations polynomiales sont également des équations rationnelles, car un polynôme peut toujours être considéré comme lui-même divisé par 1, et 1 est un polynôme d'ordre 0 (une constante).
Ce qui précède est une façon fantaisiste d'exprimer ce \(P(x) = \frac{P(x)}{1}\).
Formule d'équation rationnelle
Il n'existe pas de formule spécifique pour une équation rationnelle, mais vous devriez être en mesure de les identifier chaque fois que le quotient de deux dénominateurs apparaît dans une équation. En termes de formule, vous essayez d'identifier quelque chose comme :
\[\displaystyle \frac{P(x)}{Q(x)} \]quelque part dans l'équation, afin de la classer comme une équation rationnelle.
Comment résoudre des équations rationnelles
- Étape 1 : Assurez-vous d'abord que vous avez bien affaire à une équation rationnelle. Un autre type d'équation nécessitera très probablement une approche différente
- Étape 2 : Examinez la structure et essayez de voir si une substitution transforme rapidement l'équation en une équation polynomiale
- Étape 3 : Si une substitution rapide n'est pas possible, il faut procéder par étapes : trouver les dénominateurs communs aux deux côtés de l'équation et les multiplier par deux. Cela conduit directement à une équation polynomiale
Par exemple, si vous devez résoudre l'équation rationnelle \(\frac{1}{x} + \frac{1}{x^2} = 2\), vous pouvez utiliser la méthode plus longue qui consiste à trouver le dénominateur commun, qui dans ce cas serait \(x^2\) et vous aboutiriez à une équation polynomiale.
Mais on peut aussi faire la substitution \(u = \frac{1}{x}\), de sorte que l'équation devient l'équation auxiliaire \(u + u^2 = 2\), qui peut être résolue immédiatement à l'aide de l'équation \(u + u^2 = 2\) Formule d'équation quadratique .
Relation avec les expressions rationnelles
Les expressions rationnelles et le simplification d'une expression rationnelle est une tâche cruciale lors de la résolution d'équations impliquant des expressions rationnelles.
Mais en même temps, avant de vous lancer aveuglément dans la simplification et l'exploitation de l'équation en question, vous voudrez évaluer s'il existe ou non une substitution qui réduira les choses à une équation auxiliaire très simple.

Comment utiliser cette calculatrice d'équations rationnelles avec étapes
L'avantage de notre calculatrice est qu'elle effectue le calcul en vous montrant les étapes, ce qui peut s'avérer très utile. L'essentiel est cependant que toutes les équations rationnelles n'ont pas une solution que l'on peut trouver à l'aide de méthodes élémentaires.
Résolution d'équations il faut parfois faire preuve d'un peu de perspicacité, mais avec notre calculateur, vous n'aurez plus à vous poser de questions.

Exemple : une équation rationnelle simple
Résolvez l'équation suivante : \(\frac{1}{x} + \frac{1}{x^2} = 2\)
Solution : Nous disposons de l'équation suivante
\[\frac{1}{x}+\frac{1}{x^2}=2\]Nous utilisons la substitution : \(u = \frac{1}{x}\) pour que l'équation devienne :
\[u + u^2 = 2\]Cette équation quadratique peut être exprimée sous la forme \(u^2 + u - 2 = (u-1)(u+2) = 0\)
ce qui conduit directement aux solutions \(u = 1, u = -2\). Mais comme nous savons que \(u = \frac{1}{x}\), nous trouvons la solution suivante à l'équation originale :
\[x_1 = -\frac{1}{2} \] \[x_2 = 1 \]Par conséquent, la résolution de \(x\) pour l'équation donnée conduit aux solutions \(x=-\frac{1}{2},\,\,x=1\).
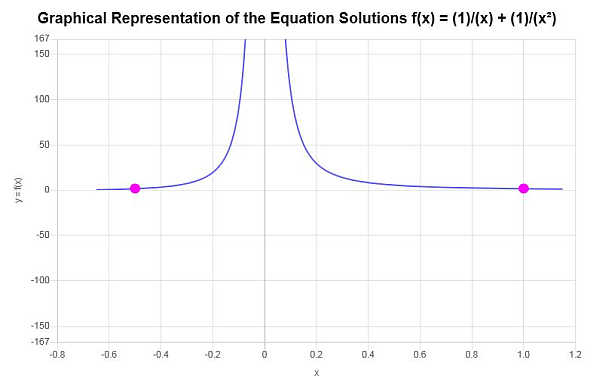
Graphiquement
La représentation graphique des solutions obtenues est la suivante :
Plus de calculatrices d'équations
La Plupart Des Calculatrices d'équations exploiteront des structures spécifiques pour tenter de trouver une solution exacte, mais leurs efforts ne seront pas toujours couronnés de succès.
Mais en fin de compte, il n'y a pas grand-chose à faire en général. La seule chose que nous pouvons faire est Résoudre des équations linéaires et résoudre des équations polynomiales (dans une certaine mesure, seulement équations quadratiques sont très simples à résoudre).
Ainsi, toute stratégie de résolution d'une équation consiste à la transformer en quelque sorte à l'aide d'une certaine réduction algébrique sont les rares types d'équations que nous savons réellement résoudre. Et la plupart du temps, tout ce que nous pouvons faire, c'est essayer quelques substitutions chanceuses, si vous êtes assez chanceux.



