Une calculatrice de fonctions

Cette calculatrice vous permet de calculer, de simplifier et de représenter graphiquement toute fonction valide que vous fournissez, en montrant toutes les étapes de simplification. Vous devez fournir une fonction valide à la calculatrice. Il peut s'agir d'une fonction déjà simplifiée comme f(x) = 2x + 3, ou d'une fonction plus complexe qui nécessite une simplification, comme f(x) = (1/3+1/4)x + x^2 - sin(1/5+1/6) + 3/4'.

Lorsqu'une fonction valide est fournie, vous pouvez simplement cliquer sur le bouton "Calculer", et le processus de simplification et d'optimisation de la fonction est lancé représentation graphique de la fonction vous sera montré.

Les fonctions sont les objets les plus importants en algèbre et en calcul, et être capable de calculer correctement et simplifier les expressions peut faire toute la différence.

Comment calculer la fonction ?

L'idée de calculer une fonction est simplement basée sur la définition d'une fonction, où pour une valeur donnée \(x\) se voit attribuer une 'image' qui est appelée \(f(x)\).

Dans le graphique ci-dessous, vous pouvez voir comment une valeur "x" sur l'axe des x se voit attribuer un point "f(x)" sur l'axe des y :

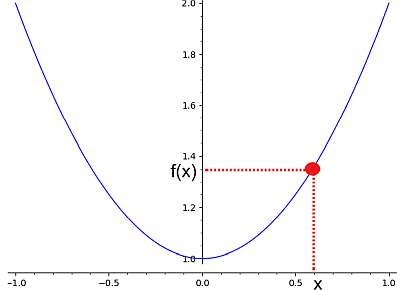
Ainsi, l'idée du calcul d'une fonction est d'obtenir une valeur "x" et d'être capable de calculer la valeur de "f(x)". Cela est parfois possible pour certaines valeurs de x, parfois pour toutes les valeurs de x sur la ligne réelle. L'ensemble des valeurs x pour lesquelles f(x) peut être calculée est appelé l'ensemble des valeurs de la ligne réelle domain d'une fonction.

Quelles sont les étapes du calcul d'une fonction ?

• Étape 1 : Identifier l'expression qui détermine la fonction
• Étape 2 : simplifiez la fonction autant que possible, mais faites attention aux divisions potentielles par zéro
• Étape 3 : noter où la fonction peut et ne peut pas être calculée

Donc, au fur et à mesure que vous avancez dans cette processus de simplification vous aurez noté toutes les valeurs pour lesquelles la fonction ne peut pas être évaluée (s'il y en a). De cette façon, vous avez indirectement trouvé le domaine de la fonction.

Par exemple, si vous avez une fonction telle que f(x) = 2x + 1, quel que soit le point que vous choisissez pour x, l'expression "2x + 1" peut toujours être évaluée. Mais au contraire, si vous avez la fonction f(x) = 1/x, si vous choisissez x = 0, vous ne pourrez pas calculer la fonction à x = 0, car cela deviendrait 1/0, et une division par zéro est indéfinie.

Comment simplifier les fonctions ?

Le processus de simplification de la fonction est comme tout autre processus de simplification simplification des expressions : vous utilisez les critères définis par le Règle de PEMDAS pour procéder à toute simplification éventuelle.

Mais il y a quelques mises en garde à faire lors de l'utilisation de PEMDAS : vous devez éviter les divisions par zéro par inadvertance, ou la prise de racines carrées de nombres négatifs. Par exemple, considérez la fonction

\[ f(x) = \displaystyle\frac{2x}{x}\]

Vous pourriez penser, eh bien, je vais annuler x, et puis j'obtiens :

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

Mais en faisant cela, vous commettez une erreur, car une telle annulation de x ne peut pas se produire lorsque x = 0. Ce que vous pouvez faire, c'est écrire explicitement

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

pour \(x \ne 0\), et indéfini pour \(x = 0\).

Quelles sont les étapes à suivre pour simplifier ?

• Étape 1 : Identifiez la fonction fournie et assurez-vous qu'il s'agit d'une expression symboliquement valide
• Étape 2 : Simplifiez les termes autant que possible en utilisant la règle PEMDAS, en veillant à ne pas obtenir de divisions par zéro ou de racines carrées négatives
• Étape 3 : Notez les points où la fonction ne peut pas être évaluée. Le domaine de la fonction sera le complément de ces points sur la droite réelle

souvent, il est assez facile de repérer les points où il pourrait y avoir un problème d'évaluation de la fonction, par simple inspection de la structure de la fonction.

Pouvez-vous calculer une fonction à partir de points ?

Cela dépend. Le processus qui consiste à trouver une fonction à partir de points donnés est appelé interpolation . Maintenant, pour un ensemble donné de points, il y aura plus d'une fonction qui passera par ces points, donc d'une certaine manière, le fait de donner les points seuls ne déterminera pas nécessairement UNE fonction.

Or, l'ajout de certaines contraintes pourrait rendre la détermination unique. Par exemple, pour deux points donnés, il n'existe qu'un seul fonction linéaire (affine linéaire, pour être plus précis) qui passe par eux. Ou encore, étant donné trois points quelconques, il n'y a qu'un seul fonction quadratique qui les traversent.

Exemple : calcul de la fonction

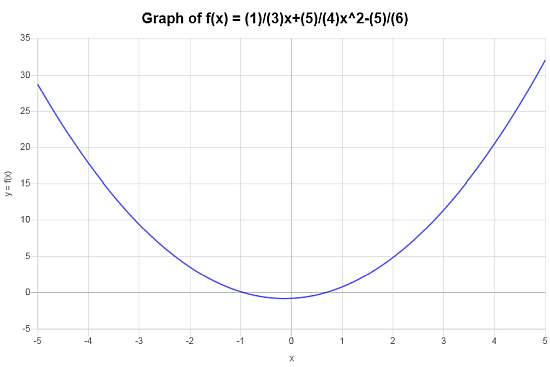
Calcul et graphique de la fonction : \(f(x) = \frac{1}{3}x + \frac{5}{4}x^2 - \frac{5}{6}\)

Solution: On a fourni la fonction suivante : \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6}\), pour laquelle nous devons simplifier et construire son graphe.

Étape 0 : Dans ce cas, nous devons d'abord simplifier la fonction donnée \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6} \), et pour ce faire, nous remarquons que :

Le tracé suivant est obtenu pour \(\displaystyle f(x)=\frac{5}{4}x^2+\frac{1}{3}x-\frac{5}{6}\) sur l'intervalle \([-5, 5]\) :

Exemple : exemple de calculatrice de fonctions

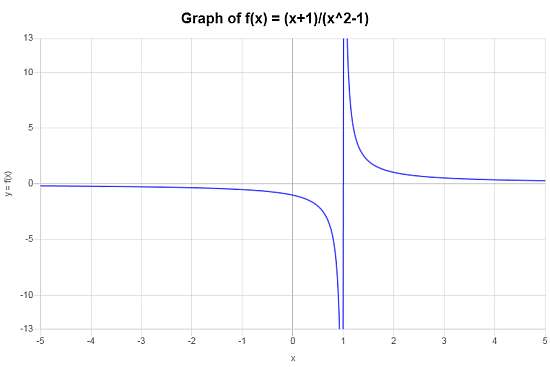
Calculez le domaine de la fonction suivante : \(f(x) = \displaystyle \frac{x+1}{x^2-1}\)

Solution: La fonction fournie \(\displaystyle f(x)=\frac{x+1}{x^2-1}\) peut être simplifiée comme suit :

\[ f(x) = \displaystyle \frac{x+1}{x^2-1} = \displaystyle \frac{x+1}{(x-1)(x+1)} = \displaystyle \frac{1}{x-1} \]

pour l'intervalle \(x \ne 1\). Par conséquent, le domaine de la fonction est \((-\infty, 1) \cup (1,\infty)\). On obtient le tracé suivant pour la fonction sur l'intervalle \([-5, 5]\) :

Exemple : un autre exemple de calculatrice de fonctions

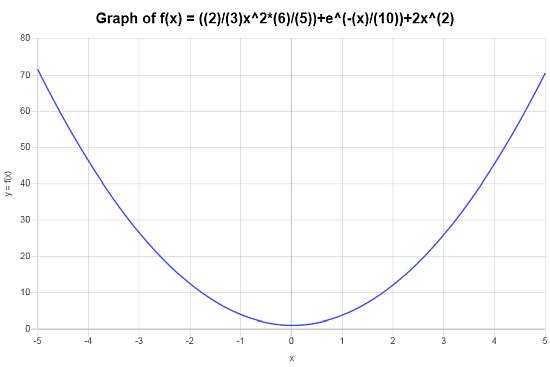
Simplifiez et représentez graphiquement \( f(x) = \left(\frac{2}{3}x^2 \times \frac{6}{5} \right)+ e^{-x/10} + 2x^2 \).

Solution: On nous fournit : \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2\). Maintenant, pour simplifier la fonction donnée \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2 \), on fait :

On obtient donc le tracé suivant pour \(\displaystyle f(x)=\frac{14}{5}x^2+e^{\left(-1/10\right)x}\) sur l'intervalle \([-5, 5]\) :

Autres calculatrices de fonctions

L'idée de fonction est centrale en algèbre et en calcul. Il y a beaucoup de choses que vous pouvez faire avec les fonctions. L'une des principales capacités que vous pouvez développer est de devenir à l'aise simplifier les expressions afin de réduire la fonction donnée en une fonction plus simple.

Assurez-vous simplement de ne pas avoir la gâchette facile et de ne pas finir par annuler les zéros et prendre les racines carrées des nombres négatifs.

Aussi, vous pouvez vouloir juste représenter graphiquement une fonction afin d'avoir une meilleure idée de l'aspect de la fonction et de ses principales propriétés.